一般的抽象系统,如社会系统、经济系统、农业系统、生态系统、教育系统等都包含有许多种因素，多种因素共同作用的结果决定了该系统的发展态势。人们常常希望知道在众多的因素中，哪些是主要因素，哪些是次要因素;哪些因素对系统发展影响大，哪些因素对系统发展影响小;哪些因素对系统发展起推动作用需强化发展,哪些因素对系统发展起阻碍作用需加以抑制;……这些都是系统分析中人们普遍关心的问题。例如,粮食生产系统，人们希望提高粮食总产量，而影响粮食总产量的因素是多方面的，有播种面积以及水利、化肥、土壤、种子、劳力、气候、耕作技术和政策环境等。为了实现少投入多产出，并取得良好的经济效益、社会效益和生态效益，就必须进行系统分析。

1.2 传统数理统计方法的不足之处

数理统计中的回归分析、方差分析、主成分分析等都是用来进行系统分析的方法。这些方法都有下述不足之处:

要求有大量数据,数据量少就难以找出统计规律;
要求样本服从某个典型的概率分布，要求各因素数据与系统特征数据之间呈线性关系且各因素之间彼此无关，这种要求往往难以满足;
计算量大，一般要靠计算机帮助;
可能出现量化结果与定性分析结果不符的现象，导致系统的关系和规律遭到歪曲和颠倒。

尤其是我国统计数据十分有限,而且现有数据灰度较大，再加上人为的原因，许多数据都出现几次大起大落，没有典型的分布规律。因此，采用数理统计方法往往难以奏效。
灰色关联分析方法弥补了采用数理统计方法作系统分析所导致的缺憾。它对样本量的多少和样本有无规律都同样适用，而且计算量小，十分方便，更不会出现量化结果与定性分析结果不符的情况。

注：数理逻辑方法才是主流，只不过本文介绍灰度关联。

1.3 灰色关联分析基本思想

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的关联度就越大，反之就越小。

1.4 系统分析

相当于找那个自变量x对y的影响最大。

对一个抽象的系统或现象进行分析，首先要选准反映系统行为特征的数据序列,称为找系统行为的映射量，用映射量来间接地表征系统行为。例如，用国民平均接受教育的年数来反映教育发达程度，用刑事案件的发案率来反映社会治安面貌和社会秩序，用医院挂号次数来反映国民的健康水平等。有了系统行为特征数据和相关因素的数据，即可作出各个序列的图形，从直观上进行分析。

--参考刘思峰. 灰⾊系统理论及其应⽤(第五版)

二、应用1：系统分析

例题：

下表为某地区国内生产总值的统计数据(以百万元计)，问该地区从2000年到2005年之间哪一种产业对GDB总量印象最大。

年份	国内生产总值	第一产业	第二产业	第三产业
2000	1988	386	839	763
2001	2061	408	846	808
2002	2335	422	960	953
2003	2750	482	1258	1010
2004	3356	511	1577	1268
2005	3806	561	1893	1352

2.1 画出统计图

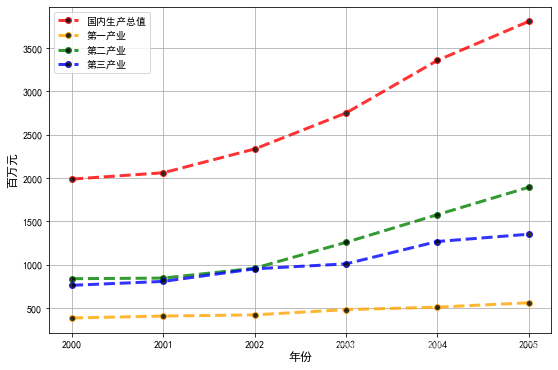
画图后得配上简单的分析 :

四个变量均呈上升的趋势
第⼆产业的增幅较为明显
第⼆产业和第三产业的差距在后三年相差增大
等等

2.2 确定分析数列

母序列(又称参考数列、母指标) : 能反映系统⾏为特征的数据序列。类似于因变量 Y , 此处记为 X。
子序列(又称⽐较数列、子指标) : 影响系统⾏为的因素组成的数据序列。类似于⾃变量X , 此处记为 $(x_{0},x_{1},...,x_{n})$ 。

在本例中国内⽣产总值就是母序列( $x_{0}$ ) , 第一二三产业就是子序列( $x_{1},x_{2},x_{3}$ )。

2.3 对变量进⾏预处理

两个目的：

去量纲
缩⼩变量范围简化计算

对母序列和子序列中的每个指标进行预处理 :

先求出每个指标的均值。
再用该指标中的每个元素都除以其均值。

预处理后：

年份	国内生产总值	第一产业	第二产业	第三产业
2000	0.7320	0.8361	0.6828	0.7439
2001	0.7588	0.8838	0.6885	0.7878
2002	0.8597	0.9141	0.7812	0.9292
2003	1.1025	1.0440	1.0237	0.9847
2004	1.2356	1.1069	1.2833	1.2363
2005	1.4013	1.2152	1.5405	1.3182

2.4 计算子序列中各个指标与母序列的关联系数

计算两极差： $|x_{0}(k)-x_{i}(k)|$

$\|x_{0}-x_{1}\|$	$\|x_{0}-x_{2}\|$	$\|x_{0}-x_{2}\|$
0.1041	0.0491	0.0119
0.1249	0.0703	0.0289
0.0543	0.0784	0.0694
0.0315	0.0112	0.0277
0.1287	0.0476	0.0006
0.1861	0.1391	0.0831

两极最小差： $a=\underset{i}{min}\: \underset{i}{min}|x_{0}(k)-x_{i}(k)|$
两极最大差： $b=\underset{i}{max}\: \underset{i}{max}|x_{0}(k)-x_{i}(k)|$

其中向量(或矩阵)x0为母序列，x123为子序列，则有： b = 0.1861, a = 0.0006，即上三列中最大的数b和最小的数a。

定义：

$y(x_{0}(k),x_{i}(k))=\frac{a+\rho b}{|x_{0}(k)-x_{i}(k)|+\rho b}$

其中 $\rho$ 为分辨系数(一般取0.5)，i=1,2,...,m ，k=1,2,...,n

则有：

$\frac{a+\rho b}{\|x_{0}(k)-x_{1}(k)\|+\rho b}$	$\frac{a+\rho b}{\|x_{0}(k)-x_{2}(k)\|+\rho b}$	$\frac{a+\rho b}{\|x_{0}(k)-x_{3}(k)\|+\rho b}$
0.4751	0.6586	0.8922
0.4298	0.5732	0.7679
0.6355	0.5461	0.5766
0.7520	0.8984	0.775
0.4223	0.6656	1.0000
0.3355	0.4035	0.5317

2.5 计算灰色关联度

定义：

$y(x_{0},x_{i})=\frac{1}{n}\sum_{i=1}^{n}y(x_{0}(k),x_{i}(k))$

也就是对上表每列求平均

灰色关联度结果为：[0.5084, 0.6242, 0.7572] 分别对应1 2 3 三个指标。

2.6 比较三个子序列和母序列的关联度得到结论

该地区在 2000年⾄ 2005年间的国内⽣产总值受到第三产业的影响最大。 (其灰色关联度最大)

惊讶了，从图上来看应该是第二产业影响最大才对：

实际上，我们最开始提到过：灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近，相应序列之间的关联度就越大，反之就越小。我们计算的结果就可以看作是在计算相似程度。

2.7 思考

1. 什么时候用标准化回归 , 什么时候用灰色关联分析 ?

当样本个数较大时, ⼀般使用标准化回归 ; 当样本个数较少时, 才使用灰⾊关联分析。

2 . 如果母序列中有多个指标, 应该怎么分析 ?

如 $Y_{1}$ $Y_2$ 是母序列， $X_1,X_2,X_3$ 是子序列，那么我们先计算 $Y_{1}$ 和 $X_1,X_2,X_3$ 的灰度分析，在计算

$Y_2$ 和 $X_1,X_2,X_3$ 的灰度分析。

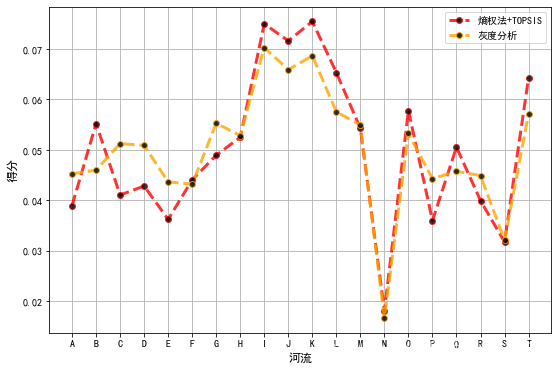
三、用于综合评价问题

老面孔，我们上一章TOPSIS法做的题：

题目：评价下表中20条河流的水质情况。

注：含氧量越高越好；PH值越接近7越好；细菌总数越少越好；植物性营养物量介于10‐20之间最佳，超过20或低于10均不好。

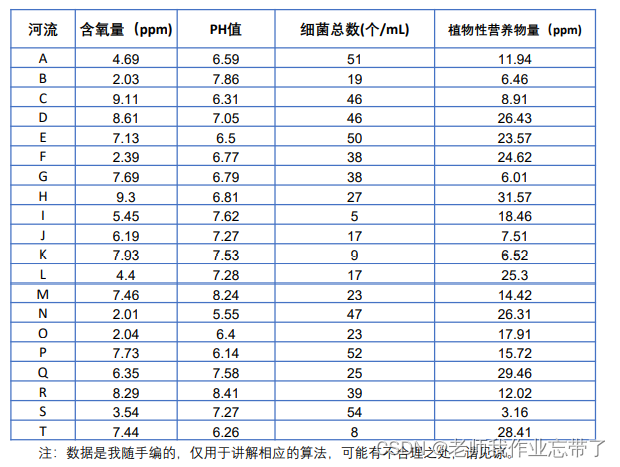
X(n*m) n=20个评价对象，m=4个评价指标。

3.1 正向化指标

之前TOPSIS所讲

含氧量越高越好；PH值越接近7越好；细菌总数越少越好；植物性营养物量介于10‐20之间最佳，超过20或低于10均不好。

3.2 对正向化后的矩阵进行预处理

每一列除以这一列的均值，目的是去除量纲缩小计算范围。

3.3 将预处理后的矩阵每行取出最大值构成母序列(虚构的)

虚构出一个Y来作为母序列，其中Y为每行各个指标的最大值。

3.4 计算各个指标与母序列的灰色关联度

计算方法同上方案例：系统分析，得到 $r_{1},\: r_{2},\: r_{3},\: ...,r_{m}$

3.5 计算各个指标的权重

$w_{i} = \frac{r_{i}}{r_1+r_2+...+r_{m}}$

3.6 第k个评价对象的得分

$S_{k}=\sum_{i=1}^{m}Z_{ki}*w_{i}, \: (k=1,...,n)$

3.7 对得分进行归一化

$S'_{i} = \frac{S_{i}}{S_{1}+S_{2}+,...,+S_{n}}$

3.8 代码

import numpy as np
import pandas as pd

data = pd.read_excel('20条河流的水质情况数据.xlsx')
matrix = data.loc[:, '含氧量（ppm)':].values

# matrix第一列是极大型指标 我们对第二三四列进行正向化
# 注：正向化的公式不唯一，大家也可以结合自己的数据进行适当的修改。

# 正向化类，这里返回拷贝后的result，也可以直接在原矩阵上进行修改。
class Index_calculation:
    def __init__(self, array):
        # 初始化指标序列
        self.array = array

    # 极小型 --> 极大型
    def samll_to_big(self):
        max_num = max(self.array)
        result = max_num - self.array
        # result = 1/self.array
        return result

    # 中间型 --> 极大型
    def middle_to_big(self, best):
        M = max(abs(self.array - best))
        result = 1 - abs(self.array - best) / M
        return result

    # 区间型 --> 极大型
    def interval_to_big(self, a, b):
        M = max([a - min(self.array), max(self.array) - b])
        result = self.array.copy()
        result[result < a] = 1 - (a - result[result < a]) / M
        result[(a < result) & (result < b) | (result == a) | (result == b)] = 1
        result[result > b] = 1 - (result[result > b] - b) / M
        return result
    
if __name__ == '__main__':
    n,m = matrix.shape

    # PH值越接近7越好
    col_2 = matrix[:, 1]
    # 细菌总数越少越好
    col_3 = matrix[:, 2]
    # 植物性营养物量介于10‐20之间最佳,超过20或低于10均不好。
    col_4 = matrix[:, 3]

    # 正向化
    matrix[:, 1] = Index_calculation(col_2).middle_to_big(7)
    matrix[:, 2] = Index_calculation(col_3).samll_to_big()
    matrix[:, 3] = Index_calculation(col_4).interval_to_big(10, 20)    
    
    # 预处理
    x = matrix/ (np.sum(matrix,axis=0)/n)

    # 把预处理后的每行最大值构成母序列(虚构的)
    y = np.max(x,axis=1)
    
    # 极差矩阵
    array = y.reshape(n,1)-x # 其实都是非负的不用求绝对值

    # 关联系数
    a = np.min(array)
    b = np.max(array)

    # 灰色关联度
    grey_d = np.mean((a+0.5*b)/(array + 0.5*b),axis=0)
    
    # 权重
    weights = grey_d/np.sum(grey_d)
    
    # 归一化前的得分
    s = np.sum(x*weights,axis=1)
    
    # 归一化后的得分
    fin_s = s/np.sum(s)

【数学模型】灰色关联分析

一、灰色关联分析概述

1.1 背景