【C++数据结构】B树概念及其实现（详解）

B树学习正式开始~~

前言

1970年，R.Bayer和E.mccreight提出了一种适合外查找的树，它是一种平衡的多叉树，称为B树。

外查找即在不在内存当中查找，通常是在磁盘，磁盘数据通常挨着挨着存，所以只能通过建立索引的方式去找到对应的数据地址。由于AVL，红黑树的高度过高，采用这类数据结构会导致IO次数过多，所以我们通常选择层数更低的B树或者B+树。

原理即是让每一层更多。并且B树天然平衡，呈现向右向上增长的趋势。

B树的规则

1. 根节点至少有两个孩子
2. 每个分支节点都包含k-1个关键字和k个孩子，其中 ceil(m/2) ≤ k ≤ m ceil是向上取整函数
3. 每个叶子节点都包含k-1个关键字，其中 ceil(m/2) ≤ k ≤ m
4. 所有的叶子节点都在同一层
5. 每个节点中的关键字从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分
6. 每个结点的结构为：（n，A0，K1，A1，K2，A2，… ，Kn，An）其中，Ki(1≤i≤n)为关键字，且Ki<Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。 n为结点中关键字的个数，满足ceil(m/2)-1≤n≤m-1。

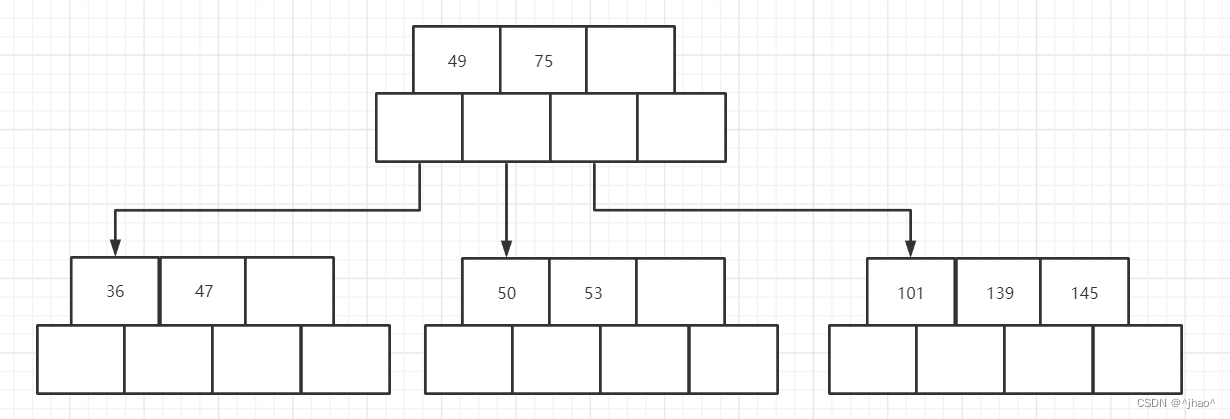
m为3为例子，我们每一个节点可以保存2个key值与3个子节点的指针，但是每个数组多开一个好处的就是便于分散。

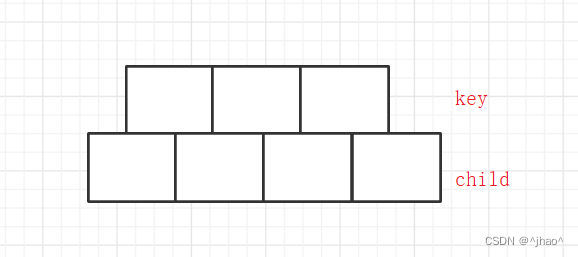
如下图当我们要插入key值为5或者是-1，我们如果不开这个长度的数组，就需要插入前做判断，但是开了数组我们可以先插入，再去分裂。

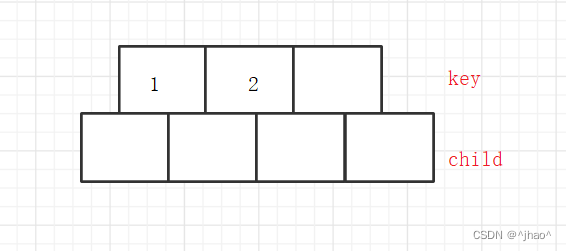
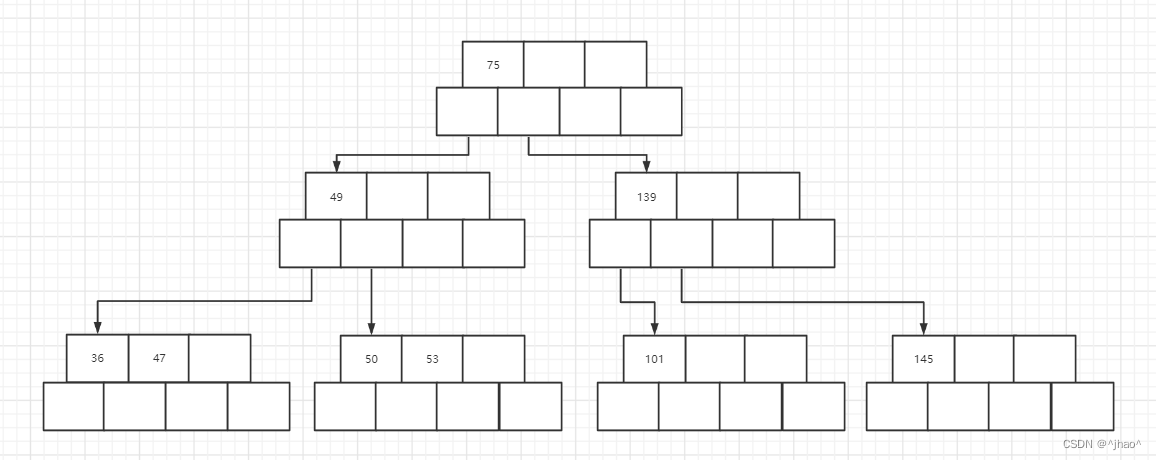
根节点最少有两孩子，可以都为NULL。

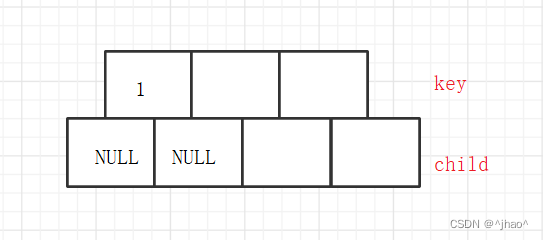
当我们多开辟一个key值与一个child指针，每次分裂恰好能满足两边的满足k-1个关键字与k个孩子。既保持孩子比关键字多一个。如m为10，则最少关键字为4，最少5个孩子，最多9个关键字，10个孩子。

注意：
同时，为了便于分裂时插入父节点，我们使用一个指针记录父节点。

节点结构设计

---

每一个节点会记录一组有效元素keys，包含着最多M-1个key值，通常这个M可以设计的比较大，如1024。还有至多M个孩子节点。一个父亲指针，以及有效元素的标识_size 因为这里的每一个节点的有效元素不同哦。。

实现当中，查找也可以采用二分查找的方式定位key值。

//K表示key值，M表示多少叉的一棵树
template<class K,size_t M>
struct BTreeNode
{
    
    
	BTreeNode()
	{
    
    
		//初始化
		for (int i = 0; i < M; ++i)
		{
    
    
			_keys[i] = K();
			_subs[i] = nullptr;
		}
		_parent = nullptr;
		//孩子比关键字多一个
		_subs[M] = nullptr;
	}
	//每一个节点掌管M个元素的数组
	K _keys[M];
	//有M+1个孩子，这里我们多开一个是为了方便进行分裂
	BTreeNode<K, M>* _subs[M+1];
	BTreeNode<K, M>* _parent;

	size_t _n = 0; // 记录实际存储多个关键字 
};

template<class K,size_t M>
	class BTree
	{
    
    
		typedef BTreeNode<K, M> Node;
	private:
		Node* _root = nullptr;
	};

以插入 53,139,75,49,145,36,50,47,101 为例子

第一次插入

---

插入53的时候

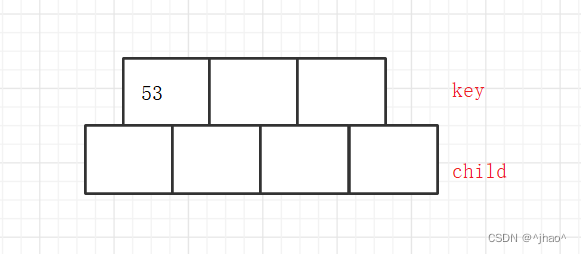
if (!_root)
{
    
    
	//一开始创建节点
	_root = new Node();

	_root->_keys[0] = key;
	_root->_n++;
	return true;
}

查找函数

---

由于插入的时候我们需要先判断是否B树已经存在该键值，我们实现的是不允许键值冗余的版本，FindKey函数提供两个功能，查找到了返回该节点和对应的下标，查找不到返回插入的位置以及-1位置。

//FindKey，找不到下标返回-1，返回可以插入的数组
//找到了返回对应的数组和下标
pair<Node*, int> FindKey(const K& key)
{
    
    
	Node* cur = _root;
	Node* parent = nullptr;
	//现在第一行寻找
	while (cur)
	{
    
    
		int i = 0;
		for (; i < cur->_n; ++i)
		{
    
    
			if (key < cur->_keys[i])
			{
    
    
				//此时去他的左孩子当中寻找
				parent = cur;
				cur = cur->_subs[i];
				break;
			}
			else if (key > cur->_keys[i])
			{
    
    
				continue;
			}
			else
			{
    
    
				//表示该元素出现在了cur这个节点，cur->_keys[i]当中。
				return std::make_pair(cur,i);
			}
		}
		//当key是当前数组的最大值
		if (cur && i == cur->_n)
		{
    
    
			//表示去最后一个节点的右孩子
			parent = cur;
			cur = cur->_subs[cur->_n];
		}
		
	}
	//走到这个位置，说明走到结尾都没有找到
	return std::make_pair(parent, -1);
}

分裂插入举例

---

依次插入到79为分裂

我们首先通过FindKey函数进行查找，通过pair的second得知没有在B树中存在，然后在pair的first当中插入key值。

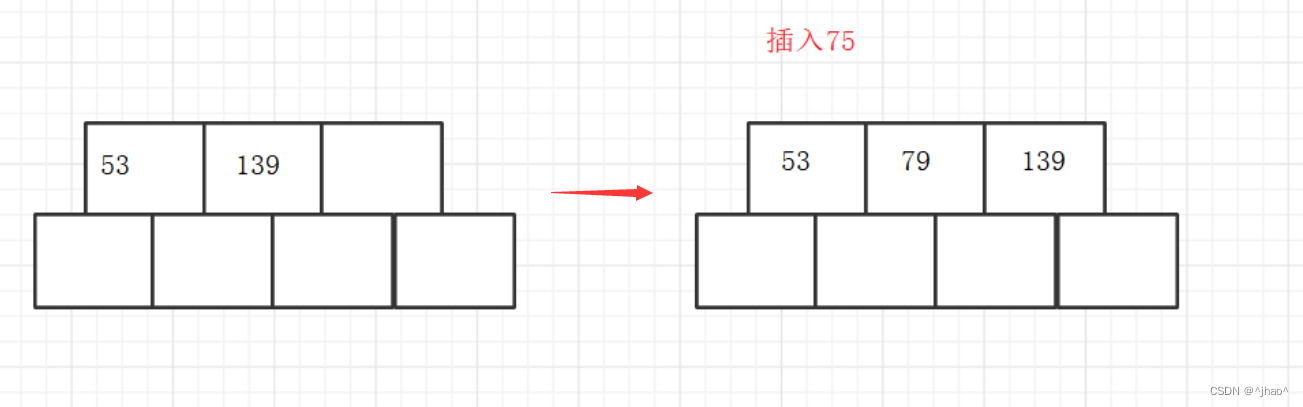
此时需要进行分裂，第一步就是将int mid = M/2保证了双边都是M-1，将[mid,cur->_n]这键值key给到brother，以及将对应key值的左右孩子指针拷贝（这里为NULL先不关心），然后将_keys[mid]也就是中间节点给到father（若不存在，则需要new一个，然后设置father的左右孩子节点，以及左右孩子节点的父亲节点都需要设置）。

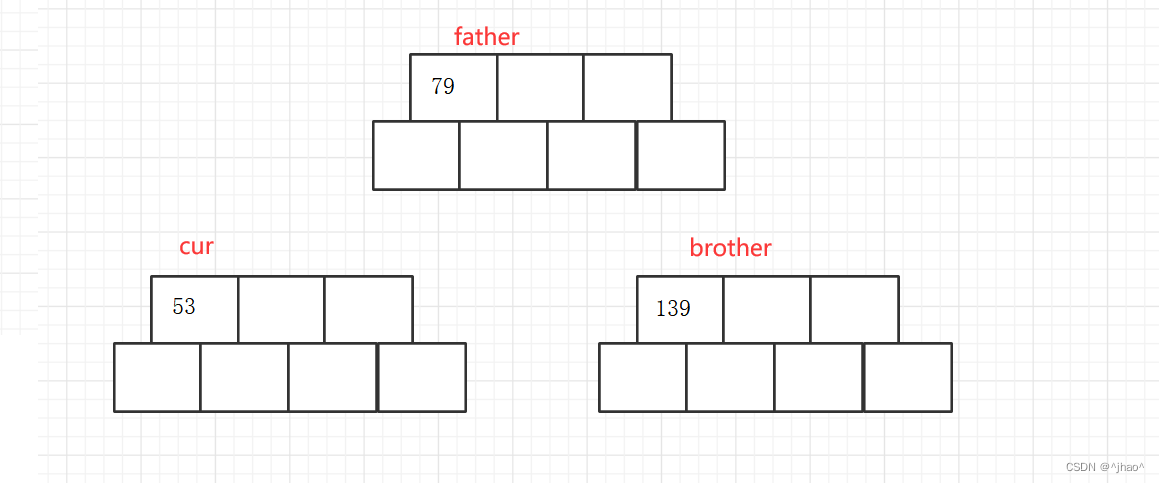
• 逻辑为先挪动键值key与孩子节点，让我们的key有位置可以插入，此时注意还需要将最后一个右孩子也给挪走
• cur->_n ！= M标识插入结束
• 若cur->_n == M则需要做以下步骤：创建兄弟节点brother，分一半的键值和孩子指针给兄弟。然后需要考虑是否已经有父亲节点（若存在，则问题转化为往父亲插入一个key值）。若不存在则只需要新创建插入key，然后将cur和brother与父亲链接起来即可。

注意：
cur->_subs[i]->_parent = brother;表示需要将分裂给brother的孩子节点重新父亲链接到brother（若存在），否则插入最后一个101的时候会观察到右子树当中的叶子节点链接不正确的情况。

void InsertKeyToNode(const K& key, Node* cur,Node* brother)
{
    
    
	//将节点往后挪，知道该位置的值小于key
	int end = cur->_n - 1;
	while (end >= 0  && cur->_keys[end] > key)
	{
    
    
		//父亲指针和数值都需要移动
		cur->_keys[end + 1] = cur->_keys[end];
		cur->_subs[end + 2] = cur->_subs[end + 1];
		end--;
	}
	//插入节点
	cur->_keys[end + 1] = key;
	if(brother)
	cur->_subs[end + 2] = brother;
	cur->_n++;

	if (cur->_n == M)
	{
    
    
		//说明此时需要分裂
		Node* brother = new Node;
		//中间节点需要往父亲提上去
		int mid = M / 2;
		K midKey = cur->_keys[mid];
		int j = 0;// 给bro用
		//tmp用于清空，便于观察
		K tmp = K();
		cur->_keys[mid] = tmp;

		for (int i = mid + 1; i < cur->_n; ++i)
		{
    
    
			//这部分数据需要移动给bro
			brother->_keys[j] = cur->_keys[i];
			//孩子需要给
			brother->_subs[j] = cur->_subs[i];
			if(cur->_subs[i])
			cur->_subs[i]->_parent = brother;
			
			//清空操作
			cur->_keys[i] = tmp;
			cur->_subs[i] = nullptr;

			j++;
		}
		brother->_parent = cur->_parent;

		//brother需要给最后一个
		brother->_n = cur->_n - mid - 1;
		cur->_n = mid;
		brother->_subs[j] = cur->_subs[cur->_n + 2];
		cur->_subs[cur->_n + 1] = nullptr;

		
		Node* parent = cur->_parent;
		//若头节点存在
		if (parent)
		{
    
    
			//问题转化为像头节点插入midKey,此时需要把brother也设置好
			InsertKeyToNode(midKey, parent,brother);
		}//若头节点不存在
		else
		{
    
    
			//中间节点提上去
			//初始化新头节点
			Node* newRoot = new Node;
			//由于是新增节点，所以需要设置他的cur和brother的父亲节点
			cur->_parent = newRoot;
			brother->_parent = newRoot;
			
			newRoot->_keys[0] = midKey;
			newRoot->_subs[0] = cur;
			newRoot->_subs[1] = brother;
			newRoot->_n++;

			_root = newRoot;
		}
	}
}

注意：插入101是一个很好的检验，通过观察就可以发现满足以下三部，先叶子节点分裂，再到_root节点的分裂产生新的根。建议根据代码调试

1.
2.
3.

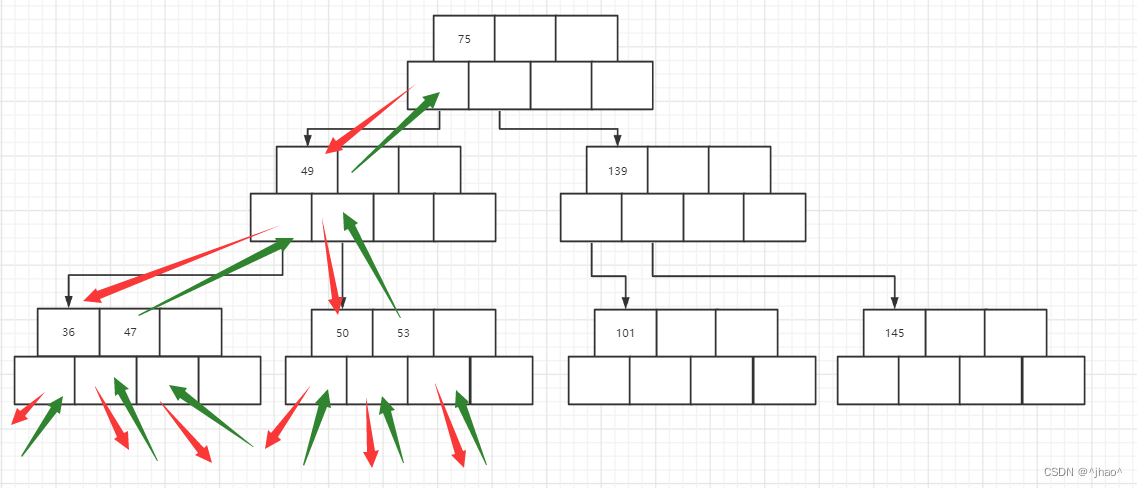
附上每一步的插入图片

插入53：

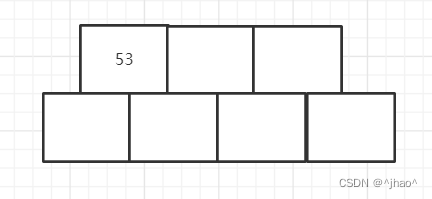
插入139：

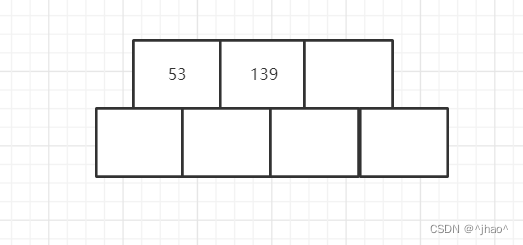
插入75：

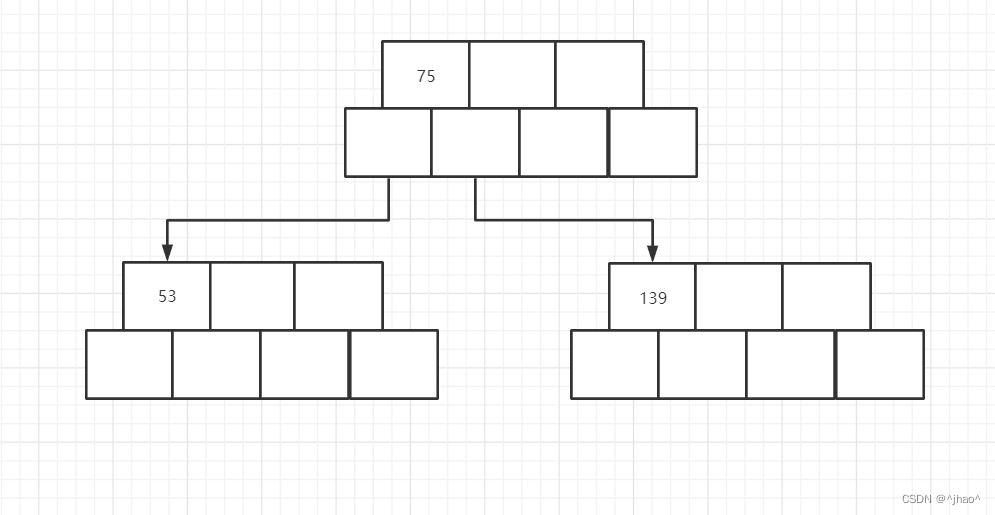
插入49：

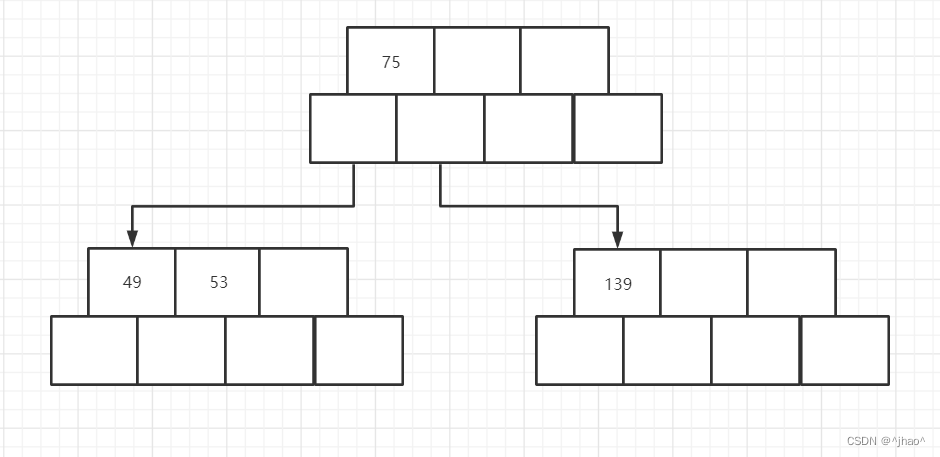
插入145：

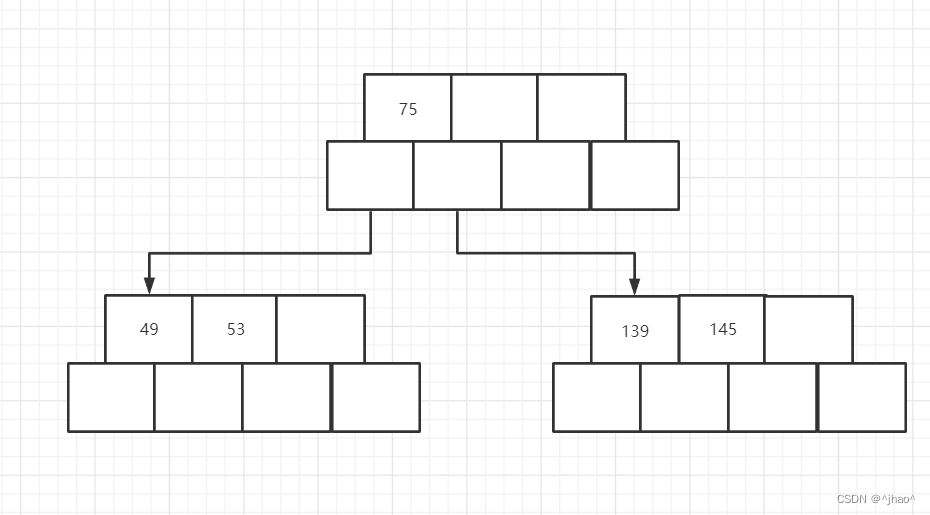
插入36：

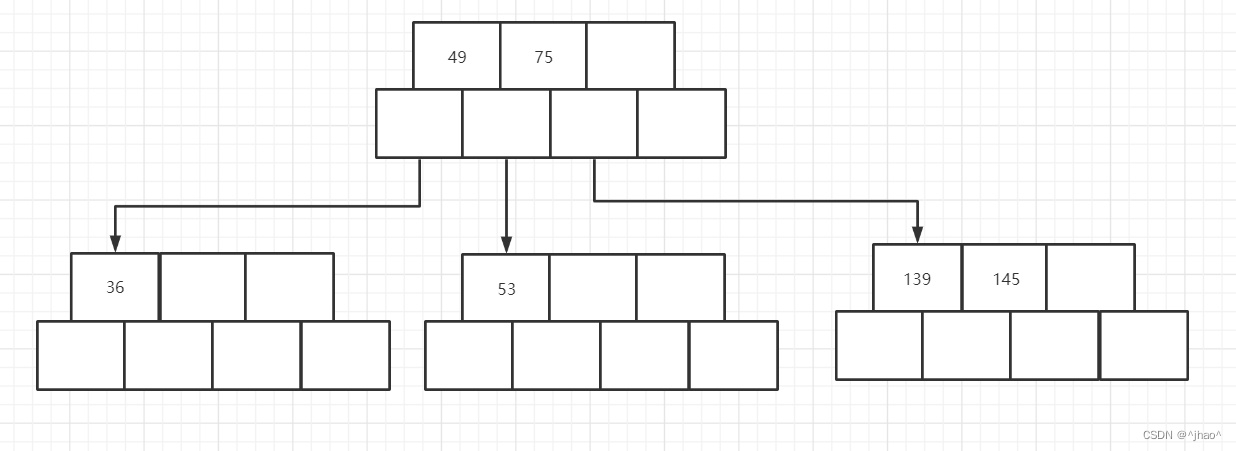
插入50：

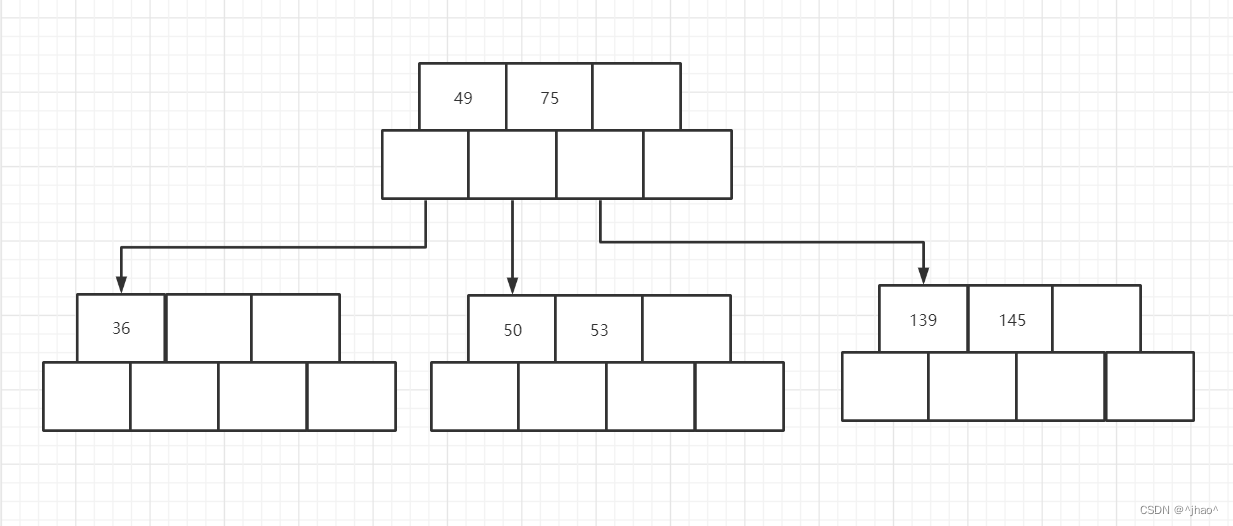
插入47：

插入101分为3步骤：

1.
2.
3.

B树效率分析

m为4的情况： 从下面二图分别有最少存放数的四层和最多存放数，可以看到第四层可以存2.5亿数据，1万亿数据。
其中每个节点的关键字按最低的算即可，算最低的时候是511，最多的时候是1023。

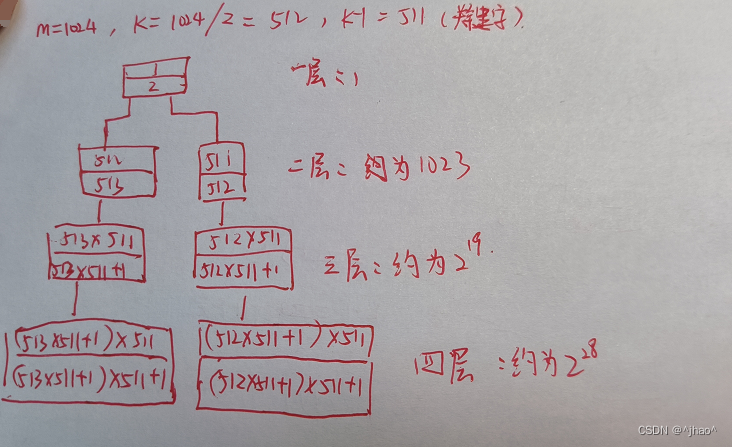
h为高度层，N为总结点数，M为每个节点的孩子数量。
M+M^2+M^3+....M^h = N
h = logmN

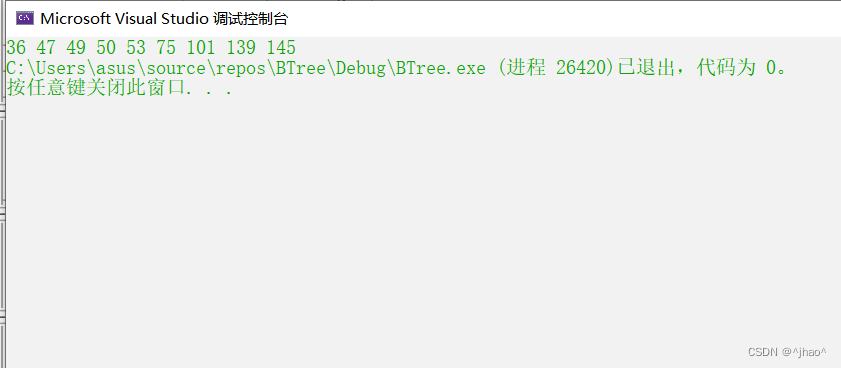
中序遍历~~

中序遍历

void Inorder()
{
    
    
	return Inorder(_root);
}
void Inorder(Node* root)
{
    
    
	if (root == nullptr)
		return;
	for (int i = 0; i < root->_n; ++i)
	{
    
    
		Inorder(root->_subs[i]);
		cout << root->_keys[i] << " ";
	}
	Inorder(root->_subs[root->_n]);
}

结果：

B+树 与 B*树

简单了解下~~

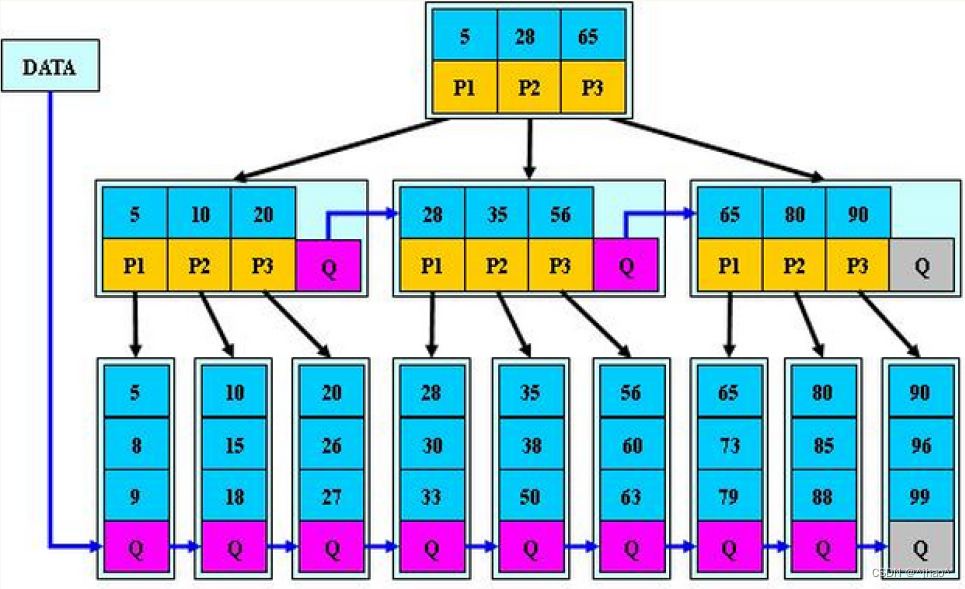
B+树

B+树对比B树在分支节点不存实际数据，将数据都放在叶子节点，并且将叶子节点用链表链接起来，方便遍历。每个分支节点不存数据会让每个分支节点能够存储更多的key值，保证了树能够进一步的压缩。

B+树添加/更新的规则：

1. 分支节点的子树指针与关键字个数相同
2. 分支节点的子树指针p[i]指向关键字值大小在[k[i]，k[i+1])区间之间(相当于取消最左边的孩子)
3. 所有叶子节点增加一个链接指针链接在一起
4. 所有关键字及其映射数据都在叶子节点出现

B+树的特性：

1. 所有关键字都出现在叶子节点的链表中，且链表中的节点都是有序的。
2. 不可能在分支节点中命中。
3. 分支节点相当于是叶子节点的索引，叶子节点才是存储数据的数据层。

B+树的分裂：
当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。

B* 树啦~~

B*树

---

B*树创建的时候是想让每个节点浪费的空间更小，由于上述的B+或者B*可能导致大量节点只用了一半的空间，导致空间浪费严重。

B*树的分裂：
当当前节点数据满了，先给部分数据给兄弟，只有兄弟也满了，才会创建新节点，两个节点都给1/3给父亲，这样就保证了每个节点空间都使用了2/3。

---

到此为止啦~

详细代码–》码云

• 喜欢就收藏
• 认同就点赞
• 支持就关注
• 疑问就评论