课程来源:吴恩达 深度学习课程 《改善神经网络》
笔记整理:王小草
时间:2018年5月26日
本文要讲的是优化算法,使你的神经网络运行得更快。
1.mini-batch梯度下降
1.1 如何得到mini-batch
可将所有样本的特征x表示成一个大矩阵,维数为(n, m),其中n为特征的维数,m为样本的总数目:
X = [x(1), x(2), ...,x(m)]
可将样本的标签y表示成一个向量,维数为(1,m):
Y = [y(1), y(2),...,y(m)]
如果使用传统的梯度下降法,则需要计算每个样本的梯度,再进行平均得到最终梯度,然后进行一步梯度下降法。显然,再样本数目非常大的时候,这样做相当费时费力,因此提出了mini-batch梯度下降的方法。做法如下:
将m个样本(比如500万个)分割成一小部分小部分(比如1000个为一个部分),这每个部分称之为mini-batch。于是,总共得到5000个mini-batch,每个mini_batch有1000个样本。
分割后的X矩阵变成了5000个X{t}小矩阵:
X{1} = [x(1), x(2), …,x(1000)]
X{2} = [x(1001), x(1002), …,x(2000)]
…
==> X = [x{1}, x{2}, ...]
分割后的Y大向量也变成了5000个小向量:
Y{1} = [y(1), y(2),…,y(1000)]
Y{2} = [y(1001), y(1002),…,y(2000)]
…
==> Y= [Y{1}, Y{2},...]
一个mini-batch的维度:
X{t} :(n, 1000)
Y{t} :(1, 1000)
1.2 如何在训练集运行 mini-batch 梯度下降
对5000组mini-batch分别进行梯度下降算法更新一次参数。
for t = 1 to 5000:
//对X{t}进行前向计算
Z[1] = W[1]X{t}+b[1]
A[1] = g[1](Z[1])
...
A[l] = g[l](Z[l])
//计算代价函数
J = 1/1000 ΣL(y^(i), y(i)) + λ/(2*1000)Σ||w[t]||2
//根据代价函数,反向传播进行梯度更新
W[l] = W[l] - αdW[l]
b[l] = b[l] - αdb[l]以上一次for循环称为one epoch of training.意味着当全部样本计算一遍之后,权重已经被更新了5000次了,而传统的梯度下降法,权重更新一次就得把所有样本都计算一遍,mini-batch梯度下降大大加快了计算效率。
1.3 理解 mini-batch 梯度下降法
如果使用传统的batch gradient decent,随着迭代次数的上升,代价曲线会下降,若有某一次迭代结果,代价曲线反而上升了,那么肯定是算法中或代码中有错了,正常情况下,cost与iterations肯定是单调递减的。
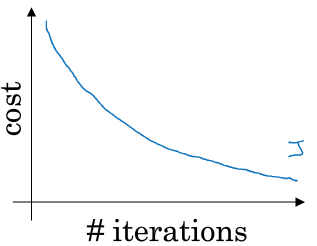
但是若使用mini-batch gradient decent,就不是一定的单调递减了,因为每次迭代中都是不同的mini-batch,样本不通过,因此会有噪声波动,但总体上的趋势肯定也是下降的。

1.4 如何选择mini-batch的大小
mini-batch size即为每个mini-batch中的样本数目
(1)if mini-batch size = m,则为传统的batch gradient descent
缺点是:训练数据太大,每一次迭代都耗时耗力。
(2)if mini-batch size = 1,则为stochstic gradient descent(即每个样本都是独立的mini-batch)
缺点是:失去所有向量化带来的加速,效率低,梯度下降过程中波动较大,且一直会在最小值附近波动,难以高效达到最小值(不过通过降低学习率,波动的噪声会稍微变小一点)
(3)实践中,一般在1~m之间取一个值做为size,那么如何选呢?
a.如果训练集很小,则直接使用batch gradient descent;
b.如果训练集很大,则使用mini-batch gradient descent,且设置的大小可以为62,128,256,512等数目(2的次方,代码会运行得更快)
c.要注意的是,你的mini-batch,X{t}, Y{t}一定要符合CPU/GPU内存,否则算法的表现将惨不忍睹。
实践中,一般会尝试几个不同的size, 然后进行比较,选择一个使得算法表现尽量高效的大小。
2.指数加权平均
接下去要介绍一些比梯度下降更有效的优化算法,在学习这些算法之前,需要用到指数加权移动平均的知识
2.1 什么是指数加权平均
以天气为例,伦敦一点自己的温度为:

换在坐标轴上如下图:

要计算温度的移动平均值,如下:
V0 = 0
V1 = 0.9V0 + 0.1θ1
V2 = 0.9V1 + 0.1θ2
V3 = 0.9V2 + 0.1θ3
…
Vt = βVt-1 + (1-β)θt
则V1,V2,…,Vt是θ1,θ2,…,θt的指数加权移动平均值
将移动平均值画出来就如下红线:
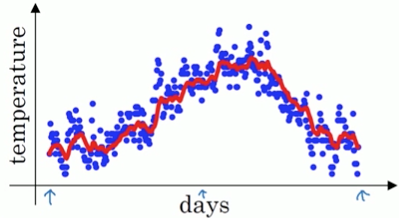
Vt可以看成是1 / (1-β) 天的近似值
当β=0.9时,Vt大约是10日的平均
当β=0.98时,Vt大约是50日的平均
当β=0.5时,Vt大约是2日的平均
若平均的天数越长,则曲线就越平滑,但总体会向右偏移。当温度变化时,指数加权平均值适应得更慢一些
2.2 理解指数加权平均
给出:
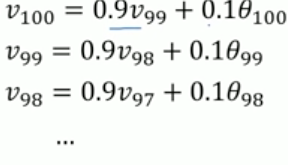
则,V100可以写成:
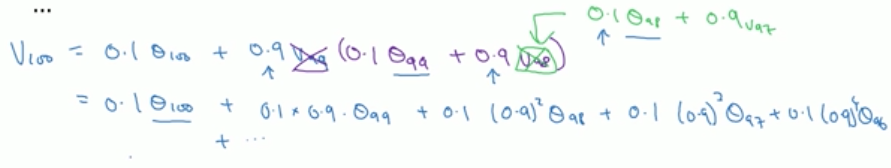
如此构造了一个指数衰减的函数,越近的温度对当日的指数移动平均文档有越大的影响,越远的数值则影响越小。
所有的系数加起来等于或接近于1,我们称之为偏差修正。
实现指数加权移动平均:
Vθ = 0
循环:
get next θt
Vt = βVt-1 + (1-β)θt2.3 指数加权平均的偏差修正
有一个技术名词,叫做“偏差修正”,它可以让指数加权平均更准确,来看看它是怎么运作的。
若Vt = βVt-1 + (1-β)θt中β=0.98,则你期望画出来的是绿色线:
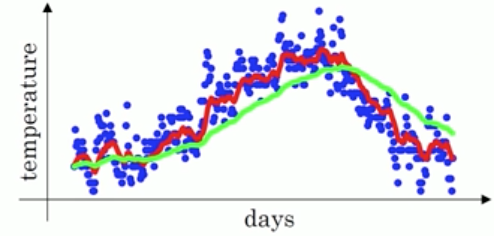
但实际上,若按照上文的步骤,画出来的是这样的紫色线:
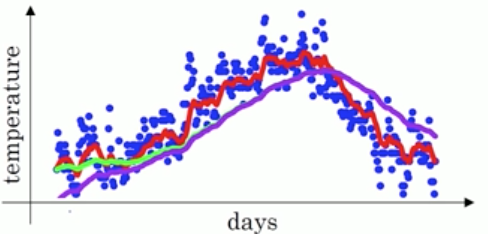
你会发现,紫色线的前面一段会比绿色线要低。那是因为我们一开始设置了V0= 0,导致V1,V2…等前面的一些数值会被估计得偏小。
那么如何解决初期估计不准的问题呢?
我们使用Vt/(1-β^t)来代替公式中的Vt。
若βt = 0.98
当t=2时,1-β^t = 1-0.98^2 = 0.0396
即V2 = V2 / 0.0396
当t很大时,1-β^t将接近与0,偏差修正几乎无作用。
通过以上修正,上图中紫线就会温和我们期待的绿线了。
3.动量梯度下降法
动量梯度下降法(Gradient descent with momentum),计算梯度的指数加权平均代替直接使用梯度,并利用加权后的梯度去更新权重。速度快于标准的梯度下降法。
当使用mini-batch低度下降法的时候有2个缺点:(1)由于每次更新梯度的样本是随机选取的不同的样本,会导致梯度在更新中波动较大,通过不断地波动才能到达最低点,(2)且必须设置一个较小的学习率(较小的学习率说明学得很慢需要更多的迭代次数),否则会偏离优化的正规。
而使用momentum就可以在一定程度上有效解决以上两个缺陷。
momentum具体的过程如下:
for i = 1 to iteration:
//计算本次mini-batch迭代中的参数梯度dw, db
dw
db
//计算加权移动平均梯度
Vdw = β*Vdw + (1-β)Vdw
Vdb = β*Vdb + (1-β)db
//更新参数
W = W - αVdw
b = b - αVdb将梯度进行移动平均之后,寻找最优点的路径的摆动就大大减少,使其能够更快找到最优点。如图,右边紫色路径是使用标准的梯度下降得到的;而左边蓝色线是使用mini-batch梯度下降得到的,会有波动;如果mini-batch中学习率设置得过大了,就会波动超级大且偏离正轨,如左边紫色线;但若使用了momentum,则会形成左边红色线的路径,即减小了波动,又能使用Mini-btch来增加迭代的效率。
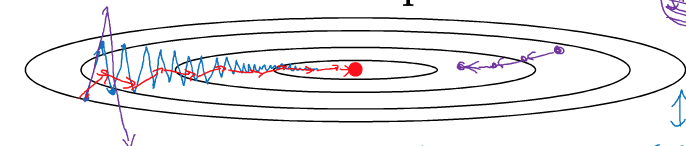
在momentum中有2个超参数:
(1)α学习率
(2)β控制指数加权平均,常用β=0.9
在momentum中因为interation很大,所以不会受到偏差的影响。
4.RMSprop
RMSprop:root mean square prop
该算法也可加速梯度下降法的效率。
上图中可以看出是一个扁平的椭圆状,由于纵向的幅度过大,导致只能使用较小的学习率,而较小的学习率就以为着收敛更慢了。而我们希望的是收敛的过程中,上下摆动能小一点,而向最低点前进的幅度能大一点,从而尽可能尽早到达最优点。这可以通过RMSprop来实现。
具体做法如下:
for i = 1 to iteration:
//计算本次mini-batch迭代中的参数梯度dw, db
dw
db
//计算指数移动平均
Sdw = β2*Sdw + (1-β2)dw^2
Sdb = β2*Sdb + (1-β2)db^2
//更新参数
W = W - α*(dw/(Sdw^(1/2)+ ε))
b = b - α*(db/(Sdb^(1/2)+ ε))其中,dw^2会是一个较小的数,db^2会是一个较大的数,
–>从而(dw/Sdw^(1/2))会较大–>W的更新会大一点
–>从而(db/Sdb^(1/2))会较小–>b的更新就会小一点
如此就实现了,W的更新大(往最低点的幅度大),b的更新小(上下摆动小),由于避免了波动,此时可以上较大的学习率也不用担心会偏离正轨了。
为了避免分母Sdw^(1/2)过小或者是一个接近于0的数,在分母上加上了一个ε系数保证数值的稳定。ε可以随意设定,一般设为10^-8
5.adam优化算法
adam:Adaptive Momentum Estimation
adam是momentum和RMSprop的结合体
废话不多说,做法如下:
Vdw = 0
Vdw = 0
Sdw = 0
Sdb = 0
for i = 1 to iteration:
//计算dw,db梯度
dw
db
//计指数移动平均算Vdw,Vdw,Sdw,Sdb
Vdw = β*Vdw + (1-β)Vdw
Vdb = β*Vdb + (1-β)db
Sdw = β2*Sdw + (1-β2)dw^2
Sdb = β2*Sdb + (1-β2)db^2
//adam中需要偏差修正
V_correct_dw = Vdw / (1-β1^t) //t是当前迭代次数
V_correct_db = Vdb / (1-β1^t)
S_correct_dw = Sdw / (1-β2^t)
S_correct_db = Sdb / (1-β2^t)
//更新参数
W = W - α*(V_correct_dw/(S_correct_dw^(1/2)+ ε))
b = b - α*(V_correct_db/(S_correct_db^(1/2)+ ε))涉及的超参数:
(1)α学习率(需要去tune寻找)
(2)β1,一般为0.9
(3)β2,一般为0.999
(4)ε,一般为10^-8
6.学习率衰减
另一个加快学习速度的方法是随着迭代次数的加深渐渐减小学习率,成为learning rate decay.
如果保持学习率不变,在快接近最优点的时候,可能还会如下图蓝线一样不断波动,绕来绕去,盲目无所适从。而若适当在接近最低优点的时候能减小学习率,就会如绿线那样,在最优点附近减少波动,从而快准狠地达到目的地
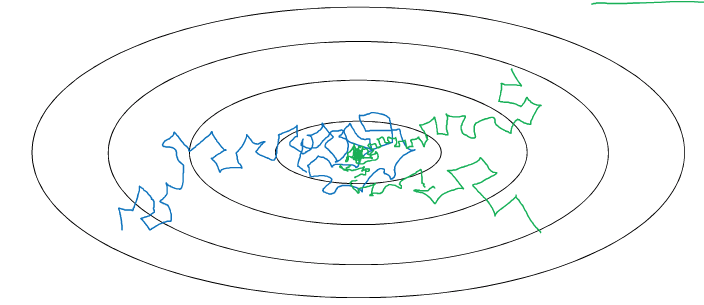
介绍常用的学习率衰减方法。
(1)method 1
在mini-batch中以epoch-num为函数的学习率
α = 1 / (1 + decay_rate * epoch_num)如此,每个epoch(一个mini-batch为一个epoch)的学习率如下:
| epoch | α |
|---|---|
| 1 | 0.1 |
| 2 | 0.67 |
| 3 | 0.5 |
| 4 | 0.4 |
| … |
(2)method 2:指数衰减(学习率程指数下降)
α = 0.95^epoch_num * α_0(3)method 3
α = ( k / square_root(epoch_num) ) * α_0
// 或者:
α = (k / square_root(t)) * α_0
(3)method 4:离散型衰减
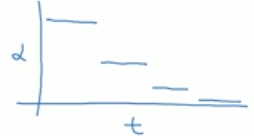
7.局部最优问题
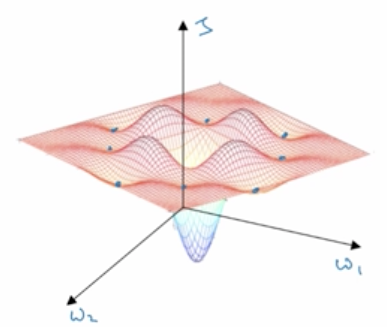
什么是局部最优,基在某一块区域内有一个最低点,但这个点并非是全局最优。若梯度下降的过程中,把局部最优点当成了全局最优点,则训练的效果将大打折扣。如下图就有很多局部最优点。
在神经网络中,给人带来困境的往往不是上面这种局部最小点,而是如下图这种鞍点(saddle points),导数为0。
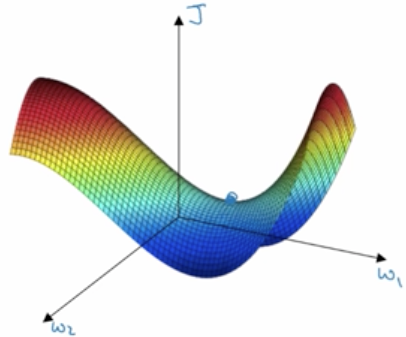
由于神经网络的维度很大,比如2万维,要形成都是凹面或凸面的组合概率很低,所以一般很难陷入图一这样局部最优的窘境。更容易遇到的是图二这样的鞍部。
既然局部最优不是神经网络的问题,那么什么神经网络会遇到的问题呢?
有一个问题,就是“平稳段(Plateau)”,平稳段会减缓学习,使得导数会长时间未0,比如酱紫;
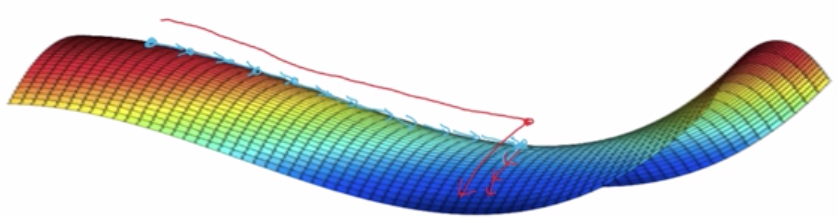
要解决平稳段问题,momentum啊,RMSprop啊,adam啊都是可以解决的。