混合正弦余弦算法和 Lévy飞行的麻雀算法
文章目录
摘要: 针对基本麻雀搜索算法抗局部最优能力弱的问题,提出了一种混合正弦余弦算法和Lévy飞行的麻雀算法(ISSA)。首先,在发现者位置更新方式中融合正弦余弦算法思想并引入非线性动态学习因子,平衡局部和全局的开掘能力,并加快收敛速度;然后,在跟随者位置更新方式中引进Lévy飞行策略,对当前最优解进行扰动变异,加强局部逃逸能力;
1.麻雀搜索算法
基础麻雀算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/108830958
2. 改进麻雀算法
2.1 融合正弦余弦算法(SCA)思想
基本 SSA 算法中,在 R 2 <ST 时,发现者随着迭代次数的进行,麻雀个体每一维都在变小,搜索空间逐渐减小,增大了坠入局部空间的概率,为改善此问题,在发现者位置更新方式中融合正弦余弦(SCA)算法思想 ,并引入非线性正弦学习因子,在搜索前期,具有较大的值,有助于全局探索,在搜索后期,具有较小的值,有助于提升局部开拓能力,提高精确度。学习因子公式和改进后的发现者位置公式如下:
ω = ω min + ( ω max − ω min ) ⋅ sin ( t π / i t e r max ) (7) \omega=\omega_{\min }+\left(\omega_{\max }-\omega_{\min }\right) \cdot \sin \left(t \pi / i t e r_{\max }\right) \tag{7} ω=ωmin+(ωmax−ωmin)⋅sin(tπ/itermax)(7)
X i , j t + 1 = { ( 1 − ω ) ⋅ X i , j t + ω ⋅ sin ( r 1 ) ⋅ ∣ r 2 ⋅ X b e t t − X i , j t ∣ R 2 < S T ( 1 − ω ) ⋅ X i , j t + ω ⋅ cos ( r 1 ) ⋅ ∣ r 2 ⋅ X b e t t − X i , j t ∣ R 2 ⩾ S T (8) X_{i, j}^{t+1}= \begin{cases}(1-\omega) \cdot X_{i, j}^{t}+\omega \cdot \sin \left(r_{1}\right) \cdot\left|r_{2} \cdot X_{b e t t}-X_{i, j}^{t}\right| & R_{2}<S T \\ (1-\omega) \cdot X_{i, j}^{t}+\omega \cdot \cos \left(r_{1}\right) \cdot\left|r_{2} \cdot X_{b e t t}-X_{i, j}^{t}\right| & R_{2} \geqslant S T\end{cases} \tag{8} Xi,jt+1={
(1−ω)⋅Xi,jt+ω⋅sin(r1)⋅∣
∣r2⋅Xbett−Xi,jt∣
∣(1−ω)⋅Xi,jt+ω⋅cos(r1)⋅∣
∣r2⋅Xbett−Xi,jt∣
∣R2<STR2⩾ST(8)
式 (8) 中, r 1 r_{1} r1 为 [ 0 , 2 π ] [0,2 \pi] [0,2π] 内的随机数, r 2 r_{2} r2 是 [ 0 , 2 ] [0,2] [0,2] 内的随机数。
2.2 Lévy飞行策略
当发现者迭代一定次数且适应度值不变时, 此 时跟随者成了发现者, 为避免算法陷人局部最优, 在跟随者更新公式中引人 Lévy飞行策略, 提高全局 搜索能力。改进后的公式如下:
X i , j t + 1 = { Q ⋅ exp ( X worst t − X i , j t i 2 ) i > n 2 X p t + 1 + X p t + 1 ⊗ Levy ( d ) other (9) X_{i, j}^{t+1}=\left\{\begin{array}{cc} Q \cdot \exp \left(\frac{X_{\text {worst }}^{t}-X_{i, j}^{t}}{i^{2}}\right) & i>\frac{n}{2} \\ X_{p}^{t+1}+X_{p}^{t+1} \otimes \operatorname{Levy}(d) & \text { other } \end{array}\right.\tag{9} Xi,jt+1={
Q⋅exp(i2Xworst t−Xi,jt)Xpt+1+Xpt+1⊗Levy(d)i>2n other (9)
式 (9)中, X p t + 1 X_{p}^{t+1} Xpt+1 是当前发现者占领的最佳位置, Lévy飞行机制如下:
Levy ( x ) = 0.01 × r 3 × σ ∣ r 4 ∣ 1 / ξ ) (10) \operatorname{Levy}(x)=0.01 \times \frac{r_{3} \times \sigma}{\left|r_{4}\right|^{1 / \xi)}}\tag{10} Levy(x)=0.01×∣r4∣1/ξ)r3×σ(10)
式 (10) 中 r 3 、 r 4 r_{3} 、 r_{4} r3、r4 均为 [ 0 , 1 ] [0,1] [0,1] 范围内的随机数, ξ \xi ξ 的值可取 1. 5, σ 计算方式如下:
σ = ( Γ ( 1 + ξ ) × sin ( π ξ / 2 ) Γ ( ( 1 + ξ ) / 2 ) × ξ × 2 ( ( ξ − 1 ) / 2 ) ) ( 1 / ξ ) (11) \sigma=\left(\frac{\Gamma(1+\xi) \times \sin (\pi \xi / 2)}{\Gamma((1+\xi) / 2) \times \xi \times 2^{((\xi-1) / 2)}}\right)^{(1 / \xi)} \tag{11} σ=(Γ((1+ξ)/2)×ξ×2((ξ−1)/2)Γ(1+ξ)×sin(πξ/2))(1/ξ)(11)
式 (11) 中 Γ ( x ) = ( x − 1 ) \Gamma(x)=(x-1) Γ(x)=(x−1) !
混合正弦余弦算法和 Lévy 飞行的麻雀算法步骤流程图如下:
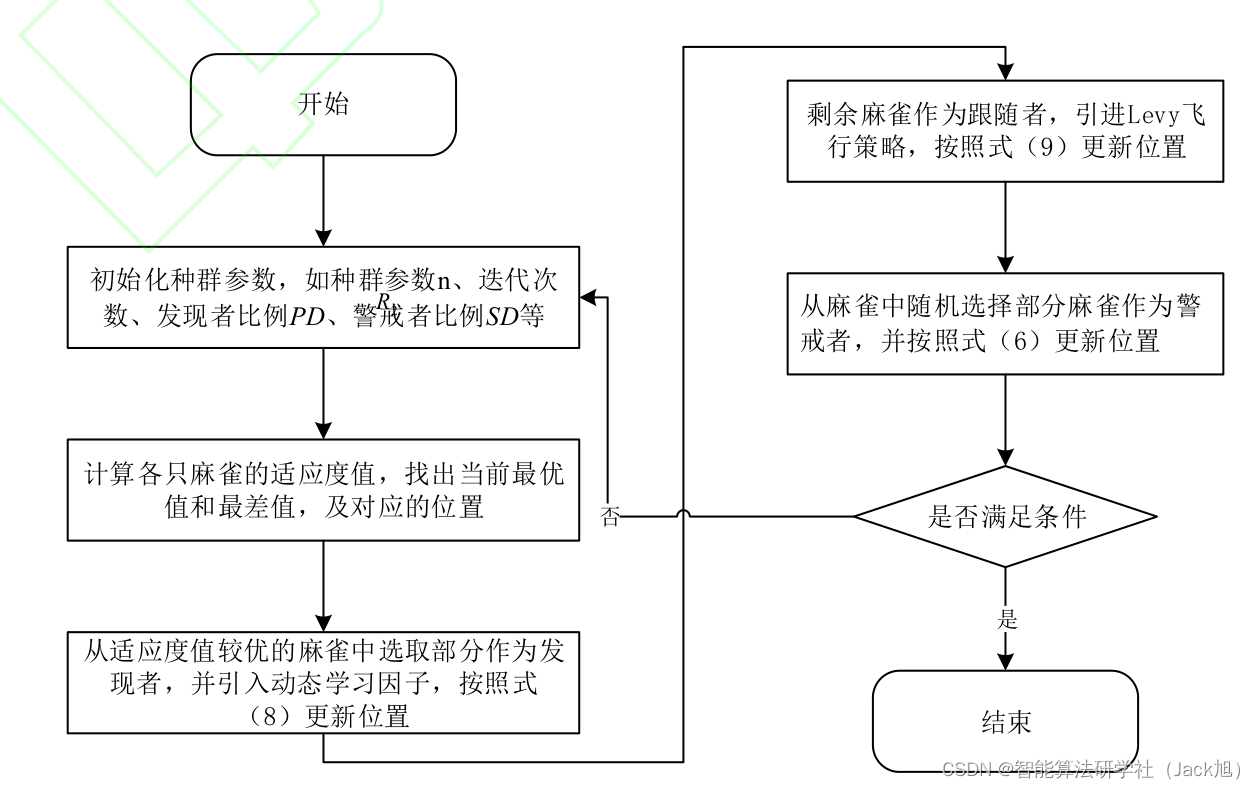
3.实验结果
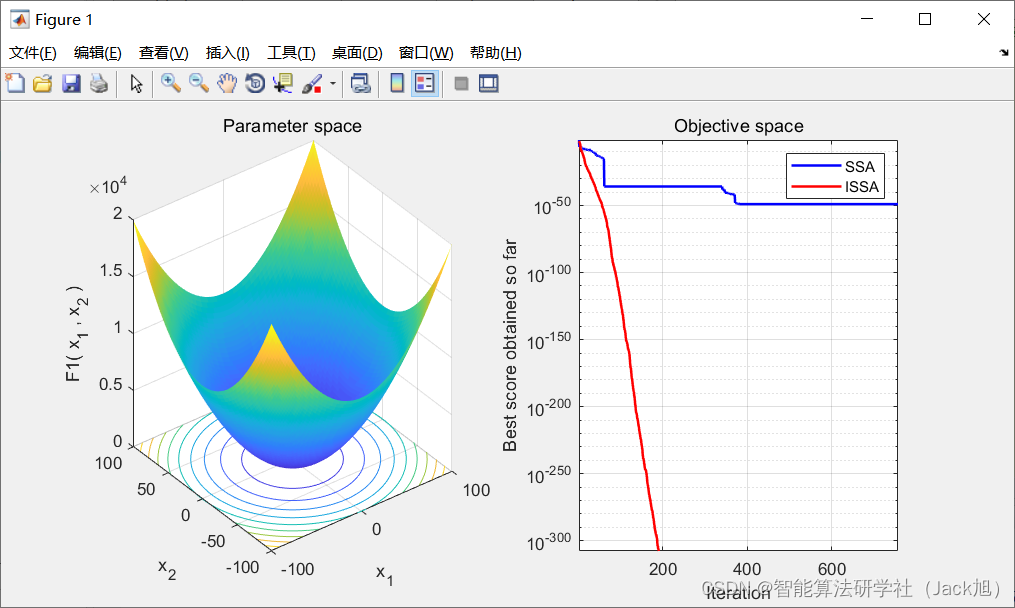
4.参考文献
[1]毛清华,张强,毛承成,柏嘉旋.混合正弦余弦算法和Lévy飞行的麻雀算法[J/OL].山西大学学报(自然科学版):1-6[2021-04-09].https://doi.org/10.13451/j.sxu.ns.2020135.