《机器学习》（周志华） 第3章 线性模型 学习心得 笔记

第3章 线性模型 学习心得

基本形式

线性模型是试图学习通过样本属性/特征的线性构成的假设函数的模型。即：
$$f(\mathbf{x})=w_1{x}_1+w_2{x}_2+\dots +w_d{x}_d+b$$
通常记为向量形式：
$$f(\mathbf{x})={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$
线性模型是机器学习中基础的模型，很多非线性模型无非是在线性模型基础上引入层级结构或者高维映射而得到。

线性回归

最小二乘法（least square method）

基于均方误差最小化进行模型求解的方法称为最小二乘法。

多元线性回归（multivariate linear regression）

数据集：
$$\mathbf{X}=\left(\begin{array}{ccccc}{x}_{11}& x_{12}& \dots & x_{1d}& 1\\ x_{21}& x_{22}& \dots & x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \dots & x_{md}& 1\end{array}\right)=\left(\begin{array}{cc}{\mathbf{x}}_1^{\mathrm{T}}& 1\\ {\mathbf{x}}_2^{\mathrm{T}}& 1\\ ⋮& ⋮\\ {\mathbf{x}}_m^{\mathrm{T}}& 1\end{array}\right)$$
对应weight：
$$\hat{\mathbf{w}}=(\mathbf{w};b)$$
由最小二乘法/均方误差最小化：
$${\hat{\mathbf{w}}}^{\ast }=\underset{\hat{\mathbf{w}}}{\mathrm{argmin}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}}{)}^{\mathrm{T}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}})$$
通过凸函数偏导数为0取得极值可得：
$$\begin{array}{c}\frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}=0-{\mathbf{X}}^{\mathrm{T}}\mathbf{y}-{\mathbf{X}}^{\mathrm{T}}\mathbf{y}+\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}+{\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)\hat{\mathbf{w}}\\ \frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}=2{\mathbf{X}}^{\mathrm{T}}(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y})\end{array}$$
其中用到了：
$$\frac{\partial {\mathbf{a}}^{\mathrm{T}}\mathbf{x}}{\partial \mathbf{x}}=\frac{\partial {\mathbf{x}}^{\mathrm{T}}\mathbf{a}}{\partial \mathbf{x}}=\mathbf{a},\frac{\partial {\mathbf{x}}^{\mathrm{T}}\mathbf{A}\mathbf{x}}{\partial \mathbf{x}}=\left(\mathbf{A}+{\mathbf{A}}^{\mathrm{T}}\right)\mathbf{x}$$
从而：
$${\hat{\mathbf{w}}}^{\ast }={\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{y}$$
这里默认了${\mathbf{X}}^{\mathrm{T}}\mathbf{X}$是满秩/正定的，而实际情况有时并不如此，则会有多解（方程个数小于未知数个数的线性方程组情况），通常可以通过加入正则化项，使得学习有一定的偏好。

对数线性回归

对于线性回归稍作推广，就可以得到非线性（对数）回归（log-linear regression）：
$$\ln y={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$

广义线性模型（generalized linear model）

$$y=g^{-1}\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right)$$
其中$g$为联系函数（link function）。上面的对数线性模型的$g$即为$\ln$。

对数几率回归/逻辑斯蒂回归（Logistic Regression）

对于线性模型产生的预测值，一般希望能够转化成二分类的标签，比如0/1，理想的一个转化是使用单位阶跃函数（unit-step function），也即delta函数的原函数：
$$y=\{\begin{array}{cl}0,& z<0\\ 0.5,& z=0\\ 1,& z>0\end{array}$$
其中，$z={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$。但是阶跃函数不连续，而我们希望其单调可微，因此需要一个替代函数（surrogate function），因此就有了对数几率函数（logistic function）：
$$y=\frac{1}{1+e^{-\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right)}}$$
也就是相当于广义线性模型中$g^{-1}(z)=\frac{1}{1+e^{-z}}$。那么由这个反函数得到原函数：
$$g(y)=\ln \frac{y}{1-y}={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$
从中可以看出，对数部分是一个相对的概率，是正例相对于反例概率的相对值，称为“几率”（odds），再加上对数运算，称为“对数几率”（log odds，或logit），所以线性回归模型逼近的就是真实标记的对数几率，因此称为对数几率回归（logistc regression，或logit regression）。
由相对概率（几率）可以定义正反例分别的概率：
$$\begin{array}{l}p(y=1\mid \mathbf{x})=\frac{e^{{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b}}{1+e^{{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b}}\\ p(y=0\mid \mathbf{x})=\frac{1}{1+e^{{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b}}\end{array}$$
写成统一的形式：
$$p\left(y_i\mid {\mathbf{x}}_i;\mathbf{w},b\right)={\left[p_1\left({\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)\right]}^{y_i}{\left[p_0\left({\hat{\mathbf{x}}}_i;\mathbf{\beta }\right)\right]}^{1-y_i}$$
从而可以得到对数似然函数：
ℓ ( β ) = ∑ i = 1 m ln ⁡ ( [ p 1 ( x ^ i ; β ) ] y i [ p 0 ( x ^ i ; β ) ] 1 − y i ) = ∑ i = 1 m [ y i ln ⁡ ( p 1 ( x ^ i ; β ) ) + ( 1 − y i ) ln ⁡ ( p 0 ( x ^ i ; β ) ) ] = ∑ i = 1 m { y i [ ln ⁡ ( p 1 ( x ^ i ; β ) ) − ln ⁡ ( p 0 ( x ^ i ; β ) ) ] + ln ⁡ ( p 0 ( x ^ i ; β ) ) } = ∑ i = 1 m [ y i ln ⁡ ( p 1 ( x ^ i ; β ) p 0 ( x ^ i ; β ) ) + ln ⁡ ( p 0 ( x ^ i ; β ) ) ] = ∑ i = 1 m [ y i ln ⁡ ( e β T x ^ i ) + ln ⁡ ( 1 1 + e β T x ^ i ) ] = ∑ i = 1 m ( y i β T x ^ i − ln ⁡ ( 1 + e β T x ^ i ) ) \begin{aligned} \ell(\boldsymbol{\beta}) &=\sum_{i=1}^{m} \ln \left(\left[p_{1}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right]^{y_{i}}\left[p_{0}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right]^{1-y_{i}}\right) \\ &=\sum_{i=1}^{m}\left[y_{i} \ln \left(p_{1}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right)+\left(1-y_{i}\right) \ln \left(p_{0}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right)\right] \\ &=\sum_{i=1}^{m}\left\{y_{i}\left[\ln \left(p_{1}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right)-\ln \left(p_{0}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right)\right]+\ln \left(p_{0}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right)\right\} \\ &=\sum_{i=1}^{m}\left[y_{i} \ln \left(\frac{p_{1}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)}{p_{0}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)}\right)+\ln \left(p_{0}\left(\hat{\boldsymbol{x}}_{i} ; \boldsymbol{\beta}\right)\right)\right] \\ &=\sum_{i=1}^{m}\left[y_{i} \ln \left(e^{\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_{i}}\right)+\ln \left(\frac{1}{1+e^{\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_{i}}}\right)\right] \\ &=\sum_{i=1}^{m}\left(y_{i} \boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_{i}-\ln \left(1+e^{\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_{i}}\right)\right) \end{aligned} ℓ(β)​=i=1∑m​ln([p1​(x^i​;β)]yi​[p0​(x^i​;β)]1−yi​)=i=1∑m​[yi​ln(p1​(x^i​;β))+(1−yi​)ln(p0​(x^i​;β))]=i=1∑m​{ yi​[ln(p1​(x^i​;β))−ln(p0​(x^i​;β))]+ln(p0​(x^i​;β))}=i=1∑m​[yi​ln(p0​(x^i​;β)p1​(x^i​;β)​)+ln(p0​(x^i​;β))]=i=1∑m​[yi​ln(eβTx^i​)+ln(1+eβTx^i​1​)]=i=1∑m​(yi​βTx^i​−ln(1+eβTx^i​))​
由于该函数是关于$\beta$的凸函数，利用梯度下降、牛顿法等可以得到全局最优解，即极大值。

线性判别分析（linear discriminant analysis，LDA）

假设了各个类别的协方差矩阵相同且满秩。其思想十分简单，对于二分类问题，将样本投影到直线上，使得同类样本投影点尽可能接近，异类样本点投影尽可能远离。如图所示：

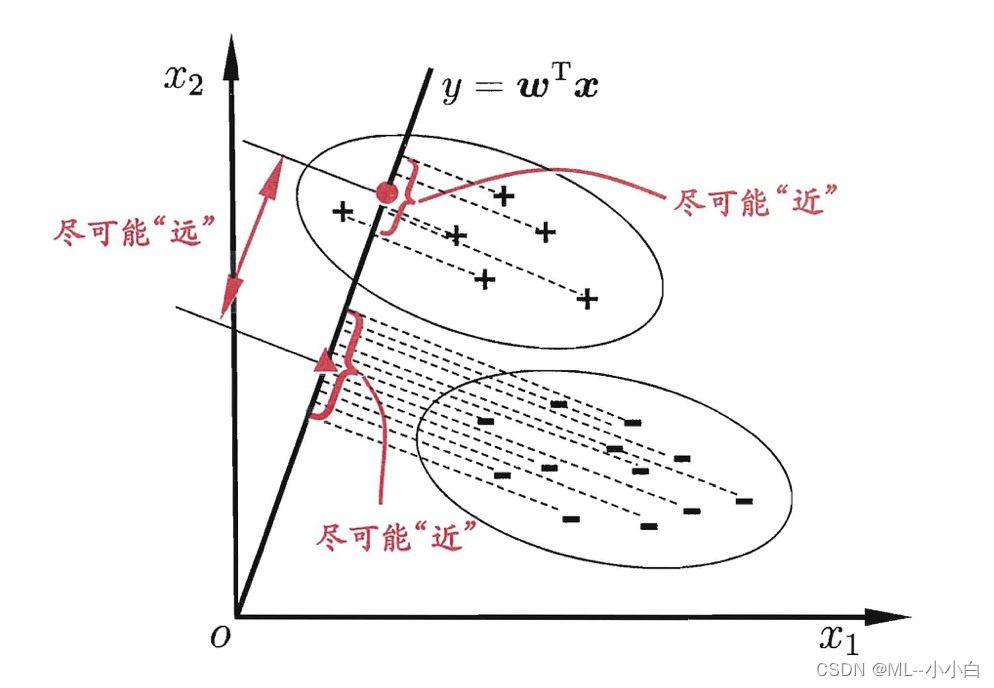
最大化目标函数为：
$$\begin{array}{rl}J& =\frac{{\Vert {\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_0-{\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_1\Vert }_2^2}{{\mathbf{w}}^{\mathrm{T}}{\mathbf{\Sigma }}_0\mathbf{w}+{\mathbf{w}}^{\mathrm{T}}{\mathbf{\Sigma }}_1\mathbf{w}}\\ & =\frac{{\mathbf{w}}^{\mathrm{T}}\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right){\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\mathbf{w}}{{\mathbf{w}}^{\mathrm{T}}\left({\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1\right)\mathbf{w}}\end{array}$$
其中分子部分表示的是将两类样本均值投影后，投影点的差距的$L_2$范数，希望它尽可能大，分母为两类中各自的方差，希望各自小，从而分母整体小，从而整个目标函数尽可能大。定义类内散度矩阵（within-class scatter matrix）$S_w$和类间散度矩阵（between-class scatter matrix）$S_b$：
$$\begin{array}{rl}{\mathbf{S}}_w& ={\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1\\ & =\sum _{\mathbf{x}\in X_0}\left(\mathbf{x}-{\mathbf{\mu }}_0\right){\left(\mathbf{x}-{\mathbf{\mu }}_0\right)}^{\mathrm{T}}+\sum _{\mathbf{x}\in X_1}\left(\mathbf{x}-{\mathbf{\mu }}_1\right){\left(\mathbf{x}-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\end{array}$$
$${\mathbf{S}}_b=\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right){\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}$$
则：
$$J=\frac{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}}{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}}$$
又称为广义瑞利商。可以发现w大小不影响结果，可约束分母为0，利用拉格朗日乘子法可得：
$${\mathbf{S}}_b\mathbf{w}=\lambda {\mathbf{S}}_w\mathbf{w}$$
在不考虑w大小的原则下，可最终取为：
$$\mathbf{w}={\mathbf{S}}_w^{-1}\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)$$
实践中，为了数值解稳定性，通常要对${\mathbf{S}}_w$进行SVD，得到${\mathbf{S}}_w=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathrm{T}}$，从而${\mathbf{S}}_w^{-1}=\mathbf{V}{\mathbf{\Sigma }}^{-1}{\mathbf{U}}^{\mathrm{T}}$。

推广到多分类

假设有N个分类，第i个类的个数为$m_i$，重新定义类内散度矩阵（within-class scatter matrix）$S_w$和类间散度矩阵（between-class scatter matrix）$S_b$：
$$\begin{array}{c}{\mathbf{S}}_w={\sum }_{i=1}^N{\mathbf{S}}_{w_i}\\ {\mathbf{S}}_{w_i}={\sum }_{\mathbf{x}\in X_i}\left(\mathbf{x}-{\mathbf{\mu }}_i\right){\left(\dot{\mathbf{x}}-{\mathbf{\mu }}_i\right)}^{\mathrm{T}}\end{array}$$
$$\begin{array}{rl}{\mathbf{S}}_t& ={\mathbf{S}}_b+{\mathbf{S}}_w\\ & =\sum _{i=1}^m\left({\mathbf{x}}_i-\mathbf{\mu }\right){\left({\mathbf{x}}_i-\mathbf{\mu }\right)}^{\mathrm{T}}\end{array}$$
$$\begin{array}{rl}{\mathbf{S}}_b& ={\mathbf{S}}_t-{\mathbf{S}}_w\\ & =\sum _{i=1}^N{m}_i\left({\mathbf{\mu }}_i-\mathbf{\mu }\right){\left({\mathbf{\mu }}_i-\mathbf{\mu }\right)}^{\mathrm{T}}\end{array}$$
其中${\mathbf{S}}_t$为全局散度矩阵。
从而可以推广广义瑞利商：
$$\underset{\mathbf{W}}{\max }\frac{{\sum }_{i=1}^{N-1}{\mathbf{w}}_i^{\mathrm{T}}{\mathbf{S}}_b{\mathbf{w}}_i}{{\sum }_{i=1}^{N-1}{\mathbf{w}}_i^{\mathrm{T}}{\mathbf{S}}_w{\mathbf{w}}_i}=\underset{\mathbf{W}}{\max }\frac{\mathrm{tr}\left({\mathbf{W}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{W}\right)}{\mathrm{tr}\left({\mathbf{W}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{W}\right)}$$
其中，$\mathbf{W}=\left({\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_i,\dots ,{\mathbf{w}}_{N-1}\right)\in {\mathbb{R}}^{d\times (N-1)}，{\mathbf{w}}_i\in {\mathbb{R}}^{d\times 1}$。
可求最优化问题：
$$\begin{array}{ll}{\min }_{\mathbf{w}}& -\mathrm{tr}\left({\mathbf{W}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{W}\right)\\ \text{ s.t. }& \mathrm{tr}\left({\mathbf{W}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{W}\right)=1\end{array}$$
从而得到：
$$\begin{array}{rl}\frac{\partial L(\mathbf{W},\lambda )}{\partial \mathbf{W}}=& -\frac{\partial \left(\mathrm{tr}\left({\mathbf{W}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{W}\right)\right)}{\partial \mathbf{W}}+\lambda \frac{\partial \left(\mathrm{tr}\left({\mathbf{W}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{W}\right)-1\right)}{\partial \mathbf{W}}\\ =& -\left({\mathbf{S}}_b+{\mathbf{S}}_b^{\mathrm{T}}\right)\mathbf{W}+\lambda \left({\mathbf{S}}_w+{\mathbf{S}}_w^{\mathrm{T}}\right)\mathbf{W}\\ =& -2{\mathbf{S}}_b\mathbf{W}+2\lambda {\mathbf{S}}_w\mathbf{W}\end{array}$$
从而：
$${\mathbf{S}}_b\mathbf{W}=\lambda {\mathbf{S}}_w\mathbf{W}$$
则$\mathbf{W}$的闭式解为${\mathbf{S}}_w^{-1}{\mathbf{S}}_b$的$d^{\prime }$个最大非零广义特征值对应的特征向量组成的矩阵，$d^{\prime }\le N-1$。

多分类学习

很多情况下，多分类是利用二分类学习实现的，比如上面的推广本质还是二分类学习。通常对于多分类学习，可以拆解成二分类，通常的拆分方法有：

一对一（one vs. one, OvO)

将数据集中的类别两两配对进行学习，预测中最终取被分类器投票最多的类别。

一对其余（One vs. Rest，OvR）

每次将数据集中的一类作为正例，其余类别均为反例，进行学习，这样学习器个数比一对一时候少很多，但是每个学习器涉及的样本数更多，最终选择分类器中预测置信度最大的预测结果。

多对多（Many vs. Many，MvM）

每次将其中几类作为正例，另外几类作为反例，但是正反例选取不随意，需要特殊设计，书上介绍了一个最常用的技术：纠错输出码（error correcting output codes，ECOC），他将编码的思想引入类别拆分，从而使得解码中有一定的容错性（联想计算机组成原理中的汉明码）

ECOC 编码/学习

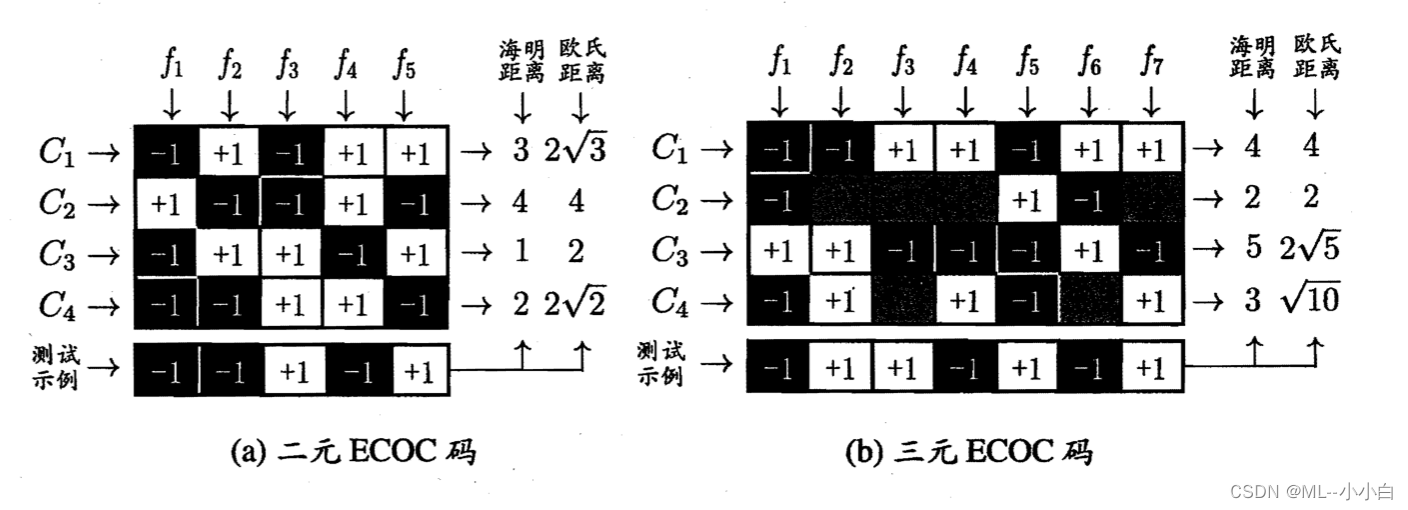
对于N个类别划分M次，每次让一部分为正类，一部分为负类，对应了M个分类器，从而有N个类各自的M位编码。学习之后形成“编码矩阵”（coding matrix），常用的为二元码和三元码（多一个停用类）。（如下图）

ECOC 解码/预测

对于要预测/测试的样本，将其经过M个分类器编码后，得到其M位编码，选择与该编码距离最小的类编编码作为对应的预测类别。（如下图）

类别不平衡问题（class- imbalance）

通常在数据集中会出现一些类别偏多，一些类别偏少的情况。在理想情况下，假如训练集是真实分布的无偏采样，那么，直接引入观测率的影响即可：
$$\frac{y}{1-y}>\frac{m^{+}}{m^{-}}$$
即，如果预测的正例相对反例几率（odds）大于观测概率就判为正例，或者可以转化为一个对于比值的再放缩（rescaling）或再平衡（rebalance）：
$$\frac{y^{\prime }}{1-y^{\prime }}=\frac{y}{1-y}\times \frac{m^{-}}{m^{+}}$$
但是“无偏采样”实际往往并不如此或者也无法确认，因此常用的应对类别不平衡的技术主要有三种：

对过多类的类欠采样（undersampling）/下采样（downsampling）

对多的类少采样，从而使训练用的数据集中各类别数相当。欠采样要注意不要随意丢弃，因为可能丢掉一些关键信息，常用的算法是EasyEnsemble，利用集成学习机制，将过多的类样本划分为几个数据集，共不同的学习器使用，从而在学习器上进行了欠采样但总体没有丢失信息。

对过少的类过采样（oversampling）/上采样（upsampling）

对少的类多采样，从而使训练用的数据集中各类别数相当。过采样注意不是重复对正例样本采样，代表性算法为SMOTE，对训练集正例的样本进行插值产生额外正例，这样做可以防止过拟合。

预测时的阈值移动（threshold-moving）

训练时还是使用原始的类别不平衡的数据集，但是预测时，将观测几率（上式）考虑进去，从而相当于进行预测阈值的放缩/平移。