机器学习笔记 - 常用概率分布

1、伯努利(Bernoulli)分布

Bernoulli 分布（Bernoulli distribution）是单个二值随机变量的分布。它由单个参数 $\phi \in [0, 1]$ 控制， $\phi$ 给出了随机变量等于1 的概率。

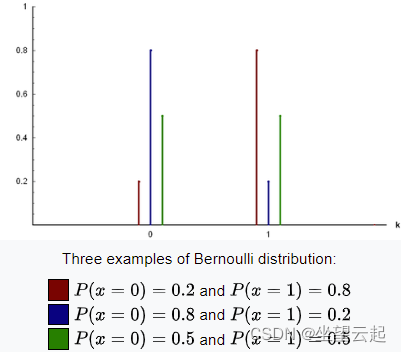
它具有如下的一些性质：

2、Multinoulli 分布

Multinoulli 分布（multinoulli distribution）或者范畴分布（categorical distribution）是指在具有k 个不同状态的单个离散型随机变量上的分布，其中k 是一个有限值。Multinoulli 分布由向量 $p \in [0, 1] ^{k-1}$ 参数化，其中每一个分量 $p_i$ 表示第 $i$ 个状态的概率。最后的第 $k$ 个状态的概率可以通过 $1 - 1^Tp$ 给出。注意我们必须限制 $1^Tp < 1$ 。Multinoulli 分布经常用来表示对象分类的分布，所以我们很少假设状态1 具有数值1 之类的。因此，我们通常不需要去计算Multinoulli 分布的随机变量的期望和方差。

Bernoulli 分布和Multinoulli 分布足够用来描述在它们领域内的任意分布。它们能够描述这些分布，不是因为它们特别强大，而是因为它们的领域很简单；它们可以对那些，能够将所有的状态进行枚举的离散型随机变量进行建模。当处理的是连续型随机变量时，会有不可数无限多的状态，所以任何通过少量参数描述的概率分布都必须在分布上加以严格的限制。

3、高斯分布

实数上最常用的分布就是正态分布（normal distribution），也称为高斯分布（Gaussian distribution）：

下图画出了正态分布的概率密度函数。

采用正态分布在很多应用中都是一个明智的选择。当我们由于缺乏关于某个实数上分布的先验知识而不知道该选择怎样的形式时，正态分布是默认的比较好的选择，其中有两个原因。

第一，我们想要建模的很多分布的真实情况是比较接近正态分布的。中心极限定理（central limit theorem）说明很多独立随机变量的和近似服从正态分布。这意味着在实际中，很多复杂系统都可以被成功地建模成正态分布的噪声，即使系统可以被分解成一些更结构化的部分。

第二，在具有相同方差的所有可能的概率分布中，正态分布在实数上具有最大的不确定性。因此，我们可以认为正态分布是对模型加入的先验知识量最少的分布。

关于正态分布可以参考下面文章进一步了解。

机器学习笔记 - 什么是标准正态分布表？自然科学和社会科学中的各类变量均呈正态分布或近似正态分布。身高、出生体重、阅读能力、工作满意度或 SAT 分数只是这些变量的几个例子。因为正态分布的变量非常普遍，所以许多统计检验都是为正态分布的总体设计的。了解正态分布的属性意味着您可以使用推论统计来比较不同的组并使用样本对总体进行估计。正态分布也称为高斯分布或钟形曲线。正态分布具有以下关键特征：均值、中位数和众数完全相同。该分布关于均值对称——一半的值低于均值，一半高于均值。均值和标准差两个值可以描述分布。https://skydance.blog.csdn.net/article/details/124118954

4、指数分布和Laplace分布

在深度学习中，我们经常需要一个在 $x=0$ 点处取得边界点(sharp point) 的分布。为了实现这一目的，我们可以使用指数分布（exponential distribution）：

指数分布使用指数函数（indicator function） $1_x \geq 0$ 来使得当x取负值的时的概率为0。

一个联系解密的概率分布是Laplace 分布（Laplace distribution），它允许我们在任意一点 $\mu$ 处设置概率质量的峰值。

5、狄拉克(Dirac)分布和经验分布

在一些情况下，我们希望概率分布中的所有质量都集中在一个点上。这可以通过Dirac delta 函数（Dirac delta function） $\delta (x)$ 定义概率密度函数来实现：

Dirac delta 函数被定义成在除了0以外的所有点的值都为0，但是积分为1。Diracdelta 函数不像普通函数一样对x 的每一个值都有一个实数值的输出，它是一种不同类型的数学对象，被称为广义函数（generalized function），广义函数是依据积分性质定义的数学对象。我们可以把Dirac delta 函数想成一系列函数的极限点，这一系列函数把除0以外的所有点的概率密度越变越小。

通过把 $p(x)$ 定义成 $\delta$ 函数左移 $-\mu$ 个单位，我们得到了一个在 $x = \mu$ 处具有无限窄也无限高的峰值的概率质量。

Dirac 分布经常作为经验分布（empirical distribution）的一个组成部分出现：

经验分布将概率密度 $1 \over m$ 赋给 $m$ 个点 $x^{(1)}...... x^{(m)}$ 中的每一个，这些点是给定的数据集或者采样的集合。只有在定义连续型随机变量的经验分布时，Dirac delta 函数才是必要的。对于离散型随机变量，情况更加简单：经验分布可以被定义成一个Multinoulli 分布，对于每一个可能的输入，其概率可以简单地设为在训练集上那个输入值的经验频率（empirical frequency）。

当我们在训练集上训练模型时，我们可以认为从这个训练集上得到的经验分布指明了我们采样来源的分布。关于经验分布另外一种重要的观点是，它是训练数据的似然最大的那个概率密度函数。

6、分布的混合

通过组合一些简单的概率分布来定义新的概率分布也是很常见的。一种通用的组合方法是构造混合分布（mixture distribution）。混合分布由一些组件(component)分布构成。每次实验，样本是由哪个组件分布产生的取决于从一个Multinoulli 分布中采样的结果，这里P(c) 是对各组件的一个Multinoulli 分布。

混合模型是组合简单概率分布来生成更丰富的分布的一种简单策略。

一个非常强大且常见的混合模型是高斯混合模型（Gaussian Mixture Model），它的组件 $p(x | c = i)$ 是高斯分布。每个组件都有各自的参数，均值 $\mu ^{(i)}$ 和协方差矩阵 $\sum ^{(i)}$ 。有一些混合可以有更多的限制。