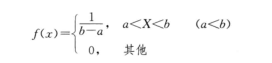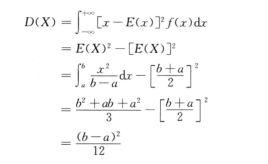统计学笔记（二）：概率和概率分布

一、概率的性质与运算法则

1.1 基本性质

对任一随机事件 $A$ ，有 $0<P(A)<1$
必然事件的概率为1，而不可能事件的概率为0，即 $P(\Omega )=1$ 、 $P(\Phi )=1$
若A与B互斥，则 $P(A\cup B)=P(A)+P(B)$ ，此性质可推广到多个两两互斥的随机事件 $A_{1},A_{2},...,A_{n}$ ，则 $P(A_{1}\cup A_{2}\cup ... \cup A_{n})=P(A_{1})+P(A_{2})+...+P(A_{n})$

1.2 运算法则

加法法则：对于任意两个随机事件，它们和的概率为两个事件分别的概率之和减去两事件相交的概率，即 $P(A\cup B)=P(A)+P(B)-P(A\cap B)$ （特别地，如果A与B互斥，则 $P(A\cap B)=0$ ，此时 $P(A\cup B)=P(A)+P(B)$ ）
乘法公式：

条件概率 $P(A|B)$ 与概率 $P(AB)$ ， $P(B)$ 有以下关系： $P(A|B)=\frac{P(AB)}{P(B)}$ ， $P(B)>0$ 另一种形式： $P(AB)=P(B)P(A|B)$ $P(AB)=P(A)P(B|A)$
独立性：两个事件中不论哪一个事件发生并不影响另一个事件发生的概率，则称这两个事件相互独立。当两个事件相互独立时，其乘法法则可以简化为： $P(AB)=P(A)P(B)$ 。多个事件 $A_{1},A_{2},...,A_{n}$ 相互独立的时候，则 $P(A_{1}A_{2}...A_{n})=P(A_{1})P(A_{2})...P(A_{n})$

二、离散型随机变量及其分布

2.1 离散型随机变量

如果随机变量 $X$ 的所有取值都可以逐个列举出来，则称X为离散型随机变量。例如：在一批产品种取到次品的个数。

2.2 离散型随机变量的概率分布

设有一离散型随机变量 $X$ ，可能取值 $x_{1},x_{2},...,x_{n}$ ，其相应的概率为 $p_{1},p_{2},...,p_{n}$ ，即 $P(X=x_{i})=p_{i}(i=1,2,...,n)$ ，如表所示：

则称该表格形式为离散型随机变量 $X$ 的概率分布（probability distribution），其中 $P(X=x_{i})=p_{i}$ 是 $X$ 的概率函数。因为 $x_{1},x_{2},...,x_{n}$ 构成一完备组，所以 $\sum_{i=1}^{n}p_{i}=1$

仅在0于1离散点的分布，称为0—1分布。

0—1分布：设离散型随机变量X只可能取0和1两个值，它的概率分布为：

$P(X=1)=p$

$P(X=0)=1-p=q$

$P(x)=p^xq^{1-x},x=0,1$

式中， $p,q>0$ 为常量， $p+q=1$ ，则称 $x$ 服从0—1分布。如下表：

2.3 离散型随机变量的期望值和方差

期望值 $E(X)$

$E(X)=x_{1}p_{1}+x_{2}p_{2}+...+x_{n}p_{n}=\sum_{i=1}^{n}x_{i}p_{i}$

（ $x_{i}$ 为随机变量X的所有可能取值， $p_{i}$ 为对应概率）

离散型随机变量 $X$ 的期望值，与加权算术平均数的写法有点类似。它表示随机变量本身的平均水平或集中程度。

方差： $\sigma ^{2}=D(X)=E[X-E(X)]^{2}$

（每一个随机变量取值于期望值的离差平方之期望值）

若 $X$ 是离散型随机变量，则 $\sigma ^2=D(X)=\sum_{i=1}^{\infty }[x_{i}-E(X)]^{2}p_{i}$

若 $X$ 的取值比较集中，则方差较小；若 $X$ 的取值比较分散，则方差较大。如果方差为0，则意味着随机变量取值集中在期望值 $E(X)$ ，即随机变量以概率1取值 $E(X)$ 。

标准差: $\sigma =\sqrt{D(X)}$

期望值反映随机变量 $X$ 取值的平均水平，方差和标准差反映随机变量 $X$ 取值的离散程度。

离散系数 $V=\frac{\sigma }{E(X)}$

用来比较不同期望值的总体之间的离中趋势。

2.4 二项分布和泊松分布

二项分布

实验只有两种结果，这种随机变量所服从的概率分布成为二项分布。比如，“成功”或“失败”，“有”和“没有”。

以 $X$ 表示n次重复独立实验中事件 $A$ （成功）出现的次数，可得：

$P(X=x)=C_{n}^{x}p^xq^{n-x},x=0,1,2,...,n$

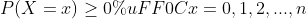
显然 $P(X=x)\geq 0，x=0,1,2,...,n$ $\sum_{x=0}^{n}C_{n}^{x}p^xq^{n-x}=(p+q)^n=1$

称随机变量 $X$ 服从二项分布，记作 $X~B(n,p)$ 。式中 $C_{n}^{x}=\frac{n!}{x!(n-x)!}$

二项分布的期望值和方差分别为：

$E(X)=np$

$D(X)=npq$

泊松分布

泊松分布是用来描述在一指定事件范围内或在指定的面积或体积之内某一事件出现的次数的分布。比较典型的服从泊松分布的随机变量的例子有：在某个企业中每月发生的事故的次数；某种仪器每月出现故障的次数。

泊松分布公式为： $P(X)=\frac{\lambda ^xe^{-\lambda}}{x!},x=1,2,...,n$ （ $\lambda$ 为给定的时间间隔内时间的平均数）

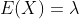
泊松分布的期望值和方差分别为： $E(X)=\lambda$ $D(X)=\lambda$

当成功的概率很小（即 $p\rightarrow 0$ ），试验次数很大时，二项分布可近似等于泊松分布，即 $C_{n}^{x}p^{x}q^{n-x}\approx \frac{\lambda ^xe^{-\lambda}}{x!}$

三、离散型随机变量及其分布

3.1 连续型随机变量

如果随机变量 $X$ 的所有取值无法逐个列举出来，而是取数轴上某一个区间内的任一点，则称 $X$ 为连续型随机变量。

3.2 概率密度与分布函数

连续型随机变量可以取某一区间或整个实数轴上的任意一个值，通常用数学函数的形式和分布函数的形式来描述。当用函数 $f(x)$ 来表示连续型随机变量时，我们将 $f(x)$ 称为概率密度函数。概率密度函数应满足以下两个条件：

(1) $f(x)\geqslant 0$ (2) $\int _{-\infty }^{+\infty}f(x)dx=1$

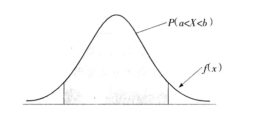
需要指出的时， $f(x)$ 并不是一个概率，即 $f(x)\neq P(X=x)$ ， $f(x)$ 称为概率密度函数，而 $P(X=x)$ 在连续分布的条件下为零。在连续分布的情况下以曲线下面的面积表示概率，如随机变量 $X$ 在 $a$ 与 $b$ 之间的概率可以写成

$P(a<X<b)=\int_{a}^{b}f(x)dx$

即下图中阴影部分的面积：

连续型随机变量的概率也可以用分布函数 $F(x)$ 来表示，分布函数定义为：

$F(x)=P(X\leqslant x)=\int_{-\infty }^{x}f(t)dt,-\infty<x<+\infty$

这也是建立在密度函数 $f(x)$ 的基础之上的，因此 $P(a<X<b)$ 也可以写成：

$\int_{a}^{b}f(x)=F(b)-F(a)$

显然，连续型随机变量的概率密度时其分布函数的导数，即 $f(x)=F'(x)$

连续型随机变量的期望值与方差分别定义为：

$E(X)=\int_{-\infty}^{+\infty}xf(x)dx=\mu$

$D(X)=\int_{-\infty}^{+\infty}[x-E(x)]^2f(x)dx=\sigma ^2$

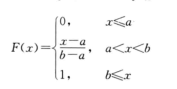
例：设连续型随机变量 $X$ 在有限区间 $(a,b)$ 内取值，其概率密度为：

试求：（1）分布函数 $F(X)$ 。（2）期望值与方差。

解：（1）由分布函数的定义可得 $F(X)=P(X\leqslant x)=\int_{-\infty}^{x}f(t)dt$

$x\leqslant a$ 时， $f(x)=0$ ，所以 $F(X)=0$

$a<x<b$ 时， $f(x)=\frac{1}{b-a}$ ，所以 $F(X)=\int_{-\infty}^{x}f(t)dt=\int_{a}^{x}\frac{1}{b-a}dt=\frac{x-a}{b-a}$

$b\leqslant x$ 时， $f(x)=0$ ，所以 $F(X)=\int_{-\infty}^{x}f(t)dt=\int_{-\infty}^{x}0dt+\int_{a}^{b}\frac{1}{b-a}dt+\int_{b}^{x}0dt=1$

所以

（2） $E(X)=\int_{-\infty}^{+\infty}xf(x)dx$

$=\int_{-\infty}^{a}0dx+\int_{a}^{b}\frac{x}{b-a}dx+\int_{b}^{+\infty}0dx$

$=\frac{1}{2}(b+a)$

（3）

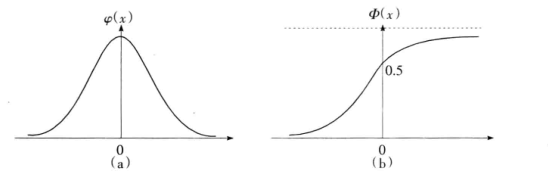
3.3 正态分布

在连续型随机变量中，最重要的一种随机变量时具有钟形概率分布的随机变量，称为正态随机变量，相应的概率分布称为正态分布（normal distribution），如下图：

在社会经济问题中，有许多随机变量的概率分布都服从正太分布。例如，某地区同年龄组儿童的发育特征，如身高、体重、肺活量；某公司年销售量等等。

如果随机变量 $X$ 的概率密度为

$f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2},-\infty<x+\infty$

则称 $X$ 服从正态分布，记作 $X\sim N(\mu,\sigma^2)$ ，其中， $-\infty<\mu+\infty$ ， $\sigma>0$ ， $\mu$ 为随机变量 $X$ 的均值， $\sigma$ 为随机变量 $X$ 的标准差，它们是正态分布的两个参数。

3.4 标准正态分布

当上式中的 $\mu=0$ ， $\sigma=1$ 时，则 $f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}},-\infty<x+\infty$

相应的正态分布 $N(0,1)$ 称为标准正态分布（standard normal distribution）。对标准正态分布，通常用 $\phi (x)$ 表示概率密度函数，用 $\Phi (x)$ 表示分布函数，即

$\phi (x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$ $\phi (x)=\int_{-\infty}^{x}\phi (t)dt=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt$