常用概率分布简介

概要

在统计分析中，经常会有假设参数服从某种分布，所以在此文中，参考《概率论与数理统计》（茆诗松著），简单罗列一下经常碰到的分布，做下简单介绍，并且结合 Python 中 Scipy.stats 模块进行模拟。将要介绍的分布目录如下：

  二项分布
  泊松分布
  正态分布
  多元正态分布
  均匀分布
  指数分布
  伽玛分布
  贝塔分布
  卡方分布
  \(F\) 分布
  \(t\) 分布

---

二项分布

描述

可以简单理解为 \(n\) 重伯努利试验中成功（概率为 \(p\)）的次数的分布，记为 \(X\)，则 \(X\) 可能取值为 \(0,1,\cdots,n\)。二项分布概率密度函数为：
\begin{align}
P(X=k) = C_n^k p^k (1-p)^{n-k}, \qquad k=0,1,2,\cdots,n
\end{align}
记为 \(X \sim b(n,p)\)。其期望、方差为：
\begin{align}
E(X) &= np \\
Var(X) &= np(1-p)
\end{align}

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import binom

fig = plt.figure()

for i, item in enumerate([(10, 0.2), (10, 0.5), (10, 0.8)]):
    n, p = item
    # stats 函数返回均值、方差、偏度、峰值，可以根据 moments 参数设置返回哪些值，
    # 其值为均值、方差、偏度、峰值的首字母，可自己随意组合，比如 'mv'，'vsk' 等
    mean, var, skew, kurt = binom.stats(n, p, moments='mvsk') 
    
    # ppf: Percent point function
    x = np.arange(binom.ppf(0.01, n, p), binom.ppf(0.99, n, p))
    
    ax = fig.add_subplot(1, 3, i+1)

    ax.spines['top'].set_visible(False)  # 设置线框不可见
    ax.spines['right'].set_visible(False)
    
    # pmf: Probability mass function
    ax.plot(x, binom.pmf(x, n, p), 'bo', ms = 8)
    
    if i == 0:
        ax.text(2.5, 0.25, u'偏度 = '+str(skew)[:5])
        ax.text(2.5, 0.23, u'峰度 = '+str(kurt)[:5])
        ax.set_xlabel(r'$b(10, 0.2)$'+u'的线条图（右偏）')
    if i == 1:
        ax.text(1.5, 0.21, u'偏度 = '+str(skew)[:5])
        ax.text(1.5, 0.19, u'峰度 = '+str(kurt)[:5])
        ax.set_xlabel(r'$b(10, 0.5)$'+u'的线条图（对称）')
    if i == 2:
        ax.text(5, 0.25, u'偏度 = '+str(skew)[:6])
        ax.text(5, 0.23, u'峰度 = '+str(kurt)[:5])
        ax.set_xlabel(r'$b(10, 0.8)$'+u'的线条图（左偏）')
        
    ax.vlines(x, 0, binom.pmf(x, n, p), 'b', lw = 5, alpha=0.5)

plt.show()

# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n    
# r = binom.rvs(n, p, loc = 0, size = 1, random_state = None )

结果如下图：

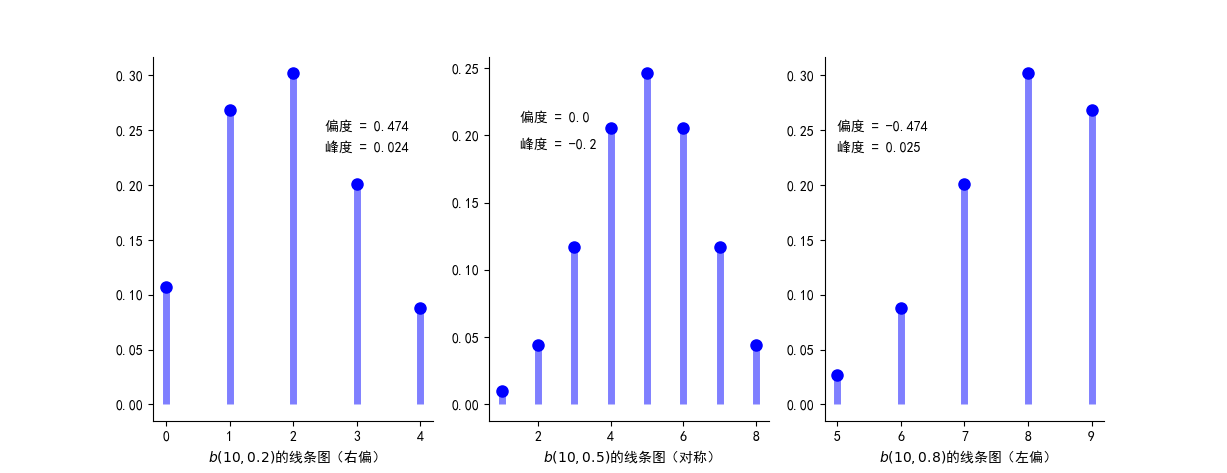
图1：二项分布 \(b(n,p)\) 的线条图

从上图可以看出：

• 位于均值 \(np\) 附近概率较大
• 随着 \(p\) 的增加，分布的峰逐渐右移

---

泊松分布

描述

泊松分布的概率分布列是
\begin{align}
P(X=k) = \frac{\lambda^k}{k!} \mathrm{e}^{-\lambda}, \qquad k=0,1,2,\cdots
\end{align}
其中参数 \(\lambda >0\)，记为 \(X \sim P(\lambda)\)。期望、方差为
\begin{align}
E(X) &= \lambda \\
Var(X) &= \lambda
\end{align}
也就是说，泊松分布 \(P(\lambda)\) 中的参数 \(\lambda\) 既是数学期望又是方差。

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import poisson

fig = plt.figure()

for i, mu in enumerate([0.8, 2.0, 4.0]):
    
    # stats 函数返回均值、方差、偏度、峰值，可以根据 moments 参数设置返回哪些值，
    # 其值为均值、方差、偏度、峰值的首字母，可自己随意组合，比如 'mv'，'vsk' 等
    mean, var, skew, kurt = poisson.stats(mu, moments='mvsk') 
    
    # ppf: Percent point function
    x = np.arange(poisson.ppf(0.01, mu), poisson.ppf(0.99, mu))
    
    ax = fig.add_subplot(1, 3, i+1)

    ax.spines['top'].set_visible(False)  # 设置线框不可见
    ax.spines['right'].set_visible(False)
    
    # pmf: Probability mass function
    ax.plot(x, poisson.pmf(x, mu), 'bo', ms = 8)
    
    if i == 0:
        ax.text(1.2, 0.3, u'偏度 = '+str(skew)[:5])
        ax.text(1.2, 0.27, u'峰度 = '+str(kurt)[:5])
        ax.set_xlabel(r'$P(0.8)$'+u'的线条图')
    if i == 1:
        ax.text(2.5, 0.22, u'偏度 = '+str(skew)[:5])
        ax.text(2.5, 0.20, u'峰度 = '+str(kurt)[:5])
        ax.set_xlabel(r'$P(2.0)$'+u'的线条图')
    if i == 2:
        ax.text(6, 0.14, u'偏度 = '+str(skew)[:6])
        ax.text(6, 0.13, u'峰度 = '+str(kurt)[:5])
        ax.set_xlabel(r'$P(4.0)$'+u'的线条图')
        
    ax.vlines(x, 0, poisson.pmf(x, mu), 'b', lw = 5, alpha=0.5)

plt.show() 
   
# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n   
# r = poisson.rvs(mu, loc = 3, size=10)

结果如下图：

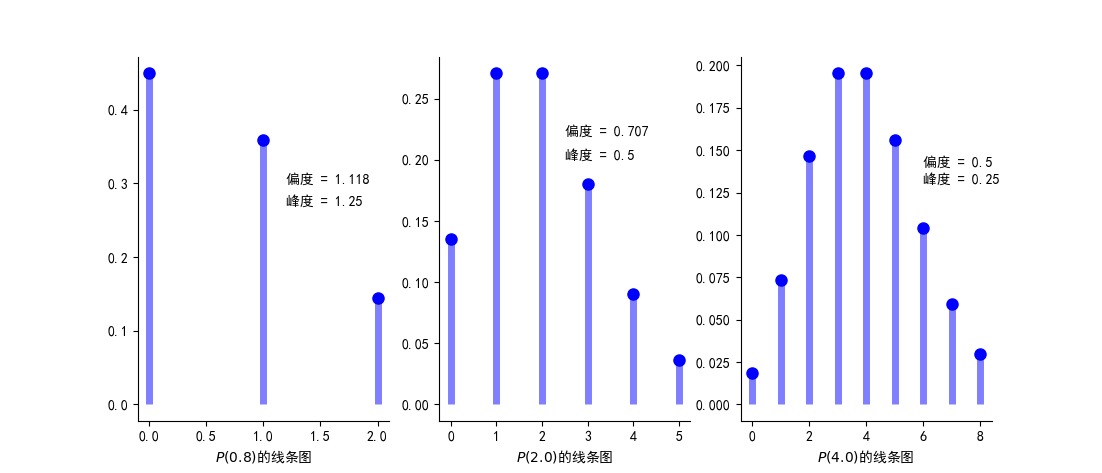
图2：泊松分布 \(P(\lambda!)\) 的线条图

从上图可以看出：

• 位于均值 \(\lambda\) 附近概率较大
• 随着 \(\lambda\) 的增加，分布逐渐趋于对称

---

正态分布

描述

正态分布的概率密度函数为：
\begin{align}
p(x) = \frac{1}{\sqrt{2\pi} \sigma} \mathrm{e}^{-\frac{(x-\mu)^2}{2\sigma^2}},\qquad -\infty < x< + \infty
\end{align}
记作 \(X \sim N(\mu, \sigma^2)\)。期望、方差分别为 \(\mu\)，\(\sigma^2\)。

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import norm

rv1 = norm(0, 0.5)  # 这样可固定参数，方便在后边直接引用
rv2 = norm(0, 1.0)
rv3 = norm(0, 1.5)


fig = plt.figure()
ax = fig.add_subplot(111)
    
# stats 函数返回均值、方差、偏度、峰值，可以根据 moments 参数设置返回哪些值，
# 其值为均值、方差、偏度、峰值的首字母，可自己随意组合，比如 'mv'，'vsk' 等
# mean, var, skew, kurt = rv1.stats(moments='mvsk') 

# ppf: Percent point function
x = np.linspace(rv1.ppf(0.01), rv1.ppf(0.99), 100)

ax.spines['top'].set_visible(False)  # 设置线框不可见
ax.spines['right'].set_visible(False)

ax.vlines(0, 0, rv1.pdf(0), lw = 5, alpha = 0.6)

ax.set_ylim(0,1)
ax.set_xticks([])

# pdf: Probability density function
ax.plot(x, rv1.pdf(x), 'r-', lw = 5, alpha = 0.6, label=r'$\sigma^2$ = 0.5')
ax.plot(x, rv2.pdf(x), 'g-', lw = 5, alpha = 0.6, label=r'$\sigma^2$ = 1.0')
ax.plot(x, rv3.pdf(x), 'b-', lw = 5, alpha = 0.6, label=r'$\sigma^2$ = 1.5')
plt.legend()
ax.set_xlabel(r'$\mu$'+u'固定，'+r'$\sigma$ 值改变')

plt.show() 
   
# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n   
# r = rv1.rvs(size=10)

结果如下图：

图3：正态密度函数

从上图可以看出：

• 如果固定 \(\mu\)，改变 \(\sigma\) 的值，则 \(\sigma\) 愈小，曲线呈高而瘦，\(\sigma\) 愈小，曲线呈矮而胖，也就是说正态密度函数的尺度由参数 \(\sigma\) 所确定，因此 \(\sigma\) 称为尺度参数。

---

多元正态分布

描述

多元正态分布的概率密度函数为：
\begin{align}
f(x) = \frac{1}{\sqrt{(2\pi)^k \mathrm{det} \, \Sigma}} \mathrm{exp} \left( - \frac{1}{2} (x-\mu)^T \Sigma^{-1} (x-\mu) \right)
\end{align}
称为 \(k\) 元随机变量 \(X\) 服从参数为 \(\mu\) 和 \(\Sigma\) 的多元正态分布，记为 \(X \sim N_k(\mu, \Sigma)\)，称 \(N_k(0, I)\) 为 \(k\) 元标准正态分布。期望、协方差分别为 \(\mu\) 和 \(\Sigma\)。其中有一个性质是 \((x-\mu)^T \Sigma^{-1} (x-\mu) \sim \mathcal{X}^2_k\)。

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import multivariate_normal

x, y = np.mgrid[-1:1:0.01, -1:1:0.01]
pos = np.dstack((x, y))

rv = multivariate_normal([0.5, -0.2], [[2.0, 0.3], [0.3, 0.5]])  # 均值和协方差

fig = plt.figure()
ax = fig.add_subplot(111)


ax.spines['top'].set_visible(False)  # 设置线框不可见
ax.spines['right'].set_visible(False)

# pdf: Probability density function
ax.contourf(x, y , rv.pdf(pos), 100, cmap = 'hot') # 100 控制等位线间距

plt.show() 

结果如下图：

图 4：二元正态分布的等位图

---

均匀分布

描述

若随机变量 \(X\) 的密度函数为
\begin{align}
p(x) = \begin{cases} \dfrac{1}{b-a}, \qquad a < x< b \\ 0, \qquad others \end{cases}
\end{align}
则称 \(X\) 服从区间 \((a,b)\) 上的均匀分布，记作 \(X \sim U(a, b)\)。其期望、方差为：
\begin{align}
E(X) &= \frac{a+b}{2} \\
Var(X)&= \frac{(b-a)^2}{12}
\end{align}

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import uniform

# ppf: Percent point function 
x = np.linspace(uniform.ppf(0.01), uniform.ppf(0.99), 100)

fig = plt.figure()
ax = fig.add_subplot(111)

ax.spines['top'].set_visible(False)  # 设置线框不可见
ax.spines['right'].set_visible(False)

rv = uniform()
# pdf: Probability density function
ax.plot(x, rv.pdf(x), 'r-', lw = 5, alpha = 0.6, label = 'uniform pdf') 
 
# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n   
r = rv.rvs(size = 1000)

ax.hist(r, normed = True, histtype = 'stepfilled', alpha = 0.2)
plt.legend()
plt.show()   

结果如下图：

图 5：均匀分布 \(U(0, 1)\) 的概率密度图

---

指数分布

描述

若随机变量 \(X\) 的密度函数为
\begin{align}
p(x) = \begin{cases} \lambda \mathrm{e}^{-\lambda x}, \qquad x \geqslant 0 \\ 0, \qquad x<0 \end{cases}
\end{align}
则称 \(X\) 服从指数分布，记作 \(X \sim Exp(\lambda)\)，其中参数 \(\lambda >0\)。其期望、方差为：
\begin{align}
E(X) &= \frac{1}{\lambda} \\
Var(X)&= \frac{1}{\lambda ^2}
\end{align}
指数分布具有无记忆性。

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import expon

# ppf: Percent point function 
x = np.linspace(expon.ppf(0.01), expon.ppf(0.99), 100)

fig = plt.figure()
ax = fig.add_subplot(111)

ax.spines['top'].set_visible(False)  # 设置线框不可见
ax.spines['right'].set_visible(False)

rv = expon()
# pdf: Probability density function
ax.plot(x, rv.pdf(x), 'r-', lw = 5, alpha = 0.6, label = 'expon pdf') 
 
# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n   
r = rv.rvs(size = 1000)

ax.hist(r, normed = True, histtype = 'stepfilled', alpha = 0.2)
plt.legend()
plt.show() 

结果如下图：

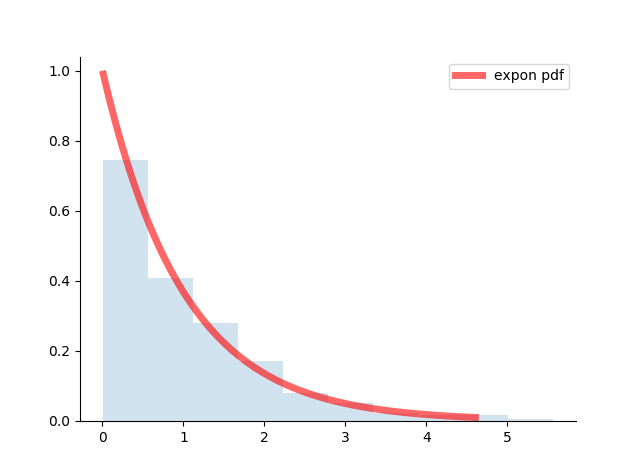
图 6：指数分布 \(Exp(1)\) 的概率密度图

---

伽玛分布

描述

称以下函数
\begin{align}
\Gamma(\alpha) = \int _0^{+\infty} x^{\alpha-1}\mathrm{e}^{-x} \, \mathrm{d}x \
\end{align}
为伽玛函数，其中参数 \(\alpha>0\)。伽玛函数具有以下性质：

• \(\Gamma(1) = 1\)，\(\Gamma(\dfrac{1}{2}) = \sqrt{\pi}\)
• \(\Gamma(\alpha+1) = \alpha \Gamma(\alpha)\)，当 \(\alpha\) 为自然数 \(n\) 时，有 \(\Gamma(n+1) = n!\)

若随机变量 \(X\) 的密度函数为
\begin{align}
p(x) = \begin{cases} \dfrac{\lambda^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} \mathrm{e}^{-\lambda x}, \qquad x \geqslant 0 \\ 0, \qquad x<0 \end{cases}
\end{align}
则称 \(X\) 服从伽玛分布，记作 \(X \sim Ga(\alpha, \lambda)\)，其中参数 \(\alpha >0\) 为形状参数，\(\lambda>0\) 为尺度参数。其期望、方差为：
\begin{align}
E(X) &= \dfrac{\alpha}{\lambda} \\
Var(X)&= \frac{\alpha}{\lambda ^2}
\end{align}
伽玛分布有两个常用的特例：

• \(\alpha=1\) 时的伽玛分布就是指数分布，即 \(Ga(1, \lambda) = Exp(\lambda)\)
• 称 \(\alpha = \dfrac{n}{2}\)，\(\lambda = \dfrac{1}{2}\) 时的伽玛分布是自由度为 \(n\) 的卡方分布，即 \(Ga(\dfrac{n}{2}, \dfrac{1}{2}) = \mathcal{X}^2(n)\)

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import gamma


rv = gamma(0.5, 1)
rv1 = gamma(1., 1)
rv2 = gamma(1.5, 1)
rv3 = gamma(2., 1)
rv4 = gamma(3., 1)

# ppf: Percent point function 
x = np.linspace(rv3.ppf(0.01), rv.ppf(0.999), 100)

fig = plt.figure()
ax = fig.add_subplot(111)

ax.spines['top'].set_visible(False)  # 设置线框不可见
ax.spines['right'].set_visible(False)

# pdf: Probability density function
ax.plot(x, rv.pdf(x), 'r-', lw = 3, alpha = 0.6, label = r'$\alpha=0.5$') 
ax.plot(x, rv1.pdf(x), 'k-', lw = 3, alpha = 0.6, label = r'$\alpha=1.0$')
ax.plot(x, rv2.pdf(x), 'b-', lw = 3, alpha = 0.6, label = r'$\alpha=1.5$')
ax.plot(x, rv3.pdf(x), 'g-', lw = 3, alpha = 0.6, label = r'$\alpha=2.0$')
ax.plot(x, rv4.pdf(x), 'c-', lw = 3, alpha = 0.6, label = r'$\alpha=3.0$')
 
# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n   
#r = rv.rvs(size = 1000)

plt.legend()
plt.show()   

结果如下图：

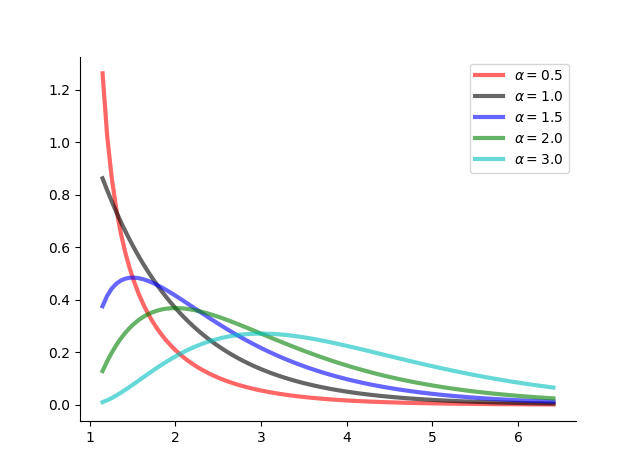
图 7：\(\lambda=1\) 固定、不同 \(\alpha\) 和伽玛密度函数曲线

从图中可以看出：

• 当 \(0<\alpha<1\) 时，\(p(x)\) 是严格下降函数，且在 \(x=0\) 处有奇异点
• 当 \(\alpha =1\) 时，\(p(x)\) 是严格下降函数，且在 \(x=0\) 处 \(p(0)=\lambda\)
• 当 \(1<\alpha \leqslant 2\) 时，\(p(x)\) 是单峰函数，先上凸、后下凸
• 当 \(2 \leqslant \alpha\) 时，\(p(x)\) 是单峰函数，先下凸、中间上凸、后下凸，且 \(\alpha\) 越大，\(p(x)\) 越近似于正态密度

---

贝塔分布

描述

称以下函数
\begin{align}
B(a,b) = \int_0^1 x^{a-1} (1-x)^{b-1} \,\mathrm{d} x
\end{align}
为贝塔函数，其中参数 \(a>0\)，\(b>0\) 。贝塔函数具有如下性质：

• \(B(a,b)=B(b,a)\)
  -\(B(a,b)=\dfrac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)}\)

若随机变量 \(X\) 的密度函数为
\begin{align}
p(x) = \begin{cases} \dfrac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)} x^{a-1}(1-x)^{b-1}, \qquad 0< x <1 \\ 0, \qquad others \end{cases}
\end{align}
则称 \(X\) 服从贝塔分布，记作 \(X \sim Be(a, b)\)，其中参数 \(a>0\)，\(b>0\)，两者都为形状参数。其期望、方差为：
\begin{align}
E(X) &= \frac{a}{a+b} \\
Var(X)&= \frac{ab}{(a+b)^2(a+b+1)}
\end{align}

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import beta

rv1 = beta(0.5, 0.5)
rv2 = beta(1.5, 1.5)
# ppf: Percent point function 
x = np.linspace(0, 1, 100)

fig = plt.figure()
ax1 = fig.add_subplot(111)

ax1.spines['top'].set_visible(False)  # 设置线框不可见
ax1.spines['right'].set_visible(False)

# pdf: Probability density function
ax1.plot(x, rv1.pdf(x), lw = 3, alpha = 0.6, label = r'$a=0.5, b=0.5$') 
ax1.plot(x, rv2.pdf(x), lw = 3, alpha = 0.6, label = r'$a=1.5, b=1.5$')
ax1.vlines(1, 0, rv1.pdf(0.999), linestyles = 'dashed', lw = 3, alpha=0.6)
ax1.legend()

# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n   
#r = rv.rvs(size = 1000)

plt.show()   

结果如下图：

图 8：均匀分布 \(U(0, 1)\) 的概率密度图

从上图可以看出：

• \(a<1,b<1\) 时，\(p(x)\) 是下凸的单峰函数
• \(a>1,b>1\) 时，\(p(x)\) 是上凸的单峰函数
• \(a<1,b\geqslant 1\) 时，\(p(x)\) 是下凸的单调减函数
• \(a\geqslant 1,b<1\) 时，\(p(x)\) 是下凸的单调增函数
• \(a=1,b=1\) 时，\(p(x)\) 是常函数，且 \(Be(1,1)=U(0,1)\)

---

卡方分布

描述

设 \(X_1,X_2, \cdots,X_n\) 独立同分布于标准正态分布 \(N(0,1)\)，则 \(\mathcal{X}^2 = X_1^2+\cdots+X_n^2\) 的分布称为自由度为 \(n\) 的 \(\mathcal{X}^2\) 分布，记为 \(\mathcal{X}^2 \sim \mathcal{X}^2(n)\)。

若 \(X \sim N(0, 1)\)，则 \(X^2 \sim Ga(\dfrac{1}{2},\dfrac{1}{2})\)，根据伽玛分布的可加独立性有 \(\mathcal{X}^2 \sim Ga(\dfrac{n}{2}, \dfrac{1}{2})=\mathcal{X}^2(n)\)，由此可见，\(\mathcal{X}^2\) 分布是伽玛分布的特例，故 \(\mathcal{X}^2(n)\) 分布 的密度函数为
\begin{align}
p(y) = \dfrac{(1/2)^{\dfrac{n}{2}}{\Gamma(n/2)}y^{\dfrac{n}{2}-1}\mathrm{e}^{-\dfrac{y}{2}}, \qquad y>0
\end{align}
该密度函数的图像是一个只取非负值的偏态分布。其期望等于自由度、方差为两倍的自由度，即：
\begin{align}
E(X) &= n \\
Var(X)&= 2n
\end{align}

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import chi2

rv1 = chi2(4)
rv2 = chi2(6)
rv3 = chi2(10)

# ppf: Percent point function 
x = np.linspace(rv2.ppf(0.01), rv2.ppf(0.99), 100)

fig = plt.figure()
ax = fig.add_subplot(111)

ax.spines['top'].set_visible(False)  # 设置线框不可见
ax.spines['right'].set_visible(False)

# pdf: Probability density function
ax.plot(x, rv1.pdf(x), lw = 3, alpha = 0.6, label = r'$n=4$') 
ax.plot(x, rv2.pdf(x), lw = 3, alpha = 0.6, label = r'$n=6$')
ax.plot(x, rv3.pdf(x), lw = 3, alpha = 0.6, label = r'$n=10$')

ax.legend()

# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n   
#r = rv.rvs(size = 1000)

plt.show()   ![]()

结果如下图：

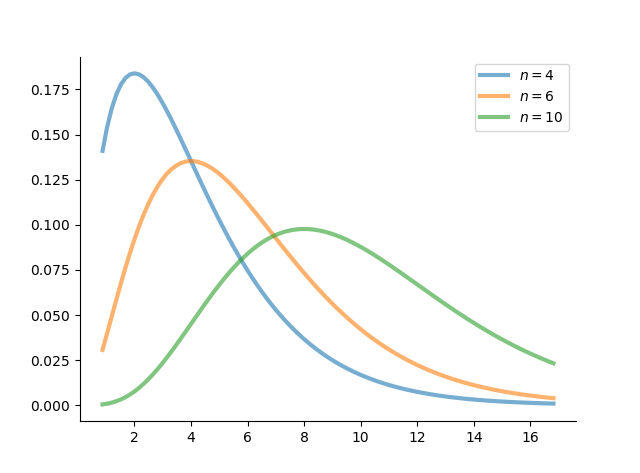
图 9：卡方分布 \(\mathcal{X}^2(n)\) 的概率密度图

---

\(F\) 分布

描述

设 \(X_1 \sim \mathcal{X}^2(m)\)， \(X_2 \sim \mathcal{X}^2(n)\)，\(X_1\) 与 \(X_2\) 独立，则称 \(F = \dfrac{X_1 / m}{X_2 / n}\) 的分布是自由度为 \(m\) 与 \(n\) 的 \(F\) 分布，记为 \(F \sim F(m,n)\)，其中 \(m\) 称为分子自由度，\(n\) 称为分母自由度。
其密度函数为
\begin{align}
p(y) = \dfrac{\Gamma\left(\dfrac{m+n}{2} \right) \left( \dfrac{m}{n}\right)^{\dfrac{m}{2}}}{\Gamma\left(\dfrac{m}{2} \right)\Gamma\left(\dfrac{n}{2} \right)} y^{\dfrac{m}{2}-1} \left( 1+ \dfrac{m}{n}y \right)^{-\dfrac{m+n}{2}} , \qquad y > 0
\end{align}
该密度函数的图像是一个只取非负值的偏态分布。由 \(F\) 分布的构造知，若 \(F\sim F(m,n)\)，则有 \(1/F \sim F(n,m)\)。经验证 \(F\) 分布的期望与方差不一定存在，详细的有待考证。

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import f

rv1 = f(4, 1)
rv2 = f(4, 4)
rv3 = f(4, 10)
rv4 = f(4, 4000)

# ppf: Percent point function 
x = np.linspace(rv2.ppf(0.01), rv2.ppf(0.9), 100)

fig = plt.figure()
ax = fig.add_subplot(111)

ax.spines['top'].set_visible(False)  # 设置线框不可见
ax.spines['right'].set_visible(False)

# pdf: Probability density function
ax.plot(x, rv1.pdf(x), lw = 3, alpha = 0.6, label = r'$m=4, n=1$') 
ax.plot(x, rv2.pdf(x), lw = 3, alpha = 0.6, label = r'$m=4, n=4$')
ax.plot(x, rv3.pdf(x), lw = 3, alpha = 0.6, label = r'$m=4, n=10$')
ax.plot(x, rv4.pdf(x), lw = 3, alpha = 0.6, label = r'$m=4, n=4000$')

ax.legend()

# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n   
#r = rv.rvs(size = 1000)

plt.show()   

结果如下图：

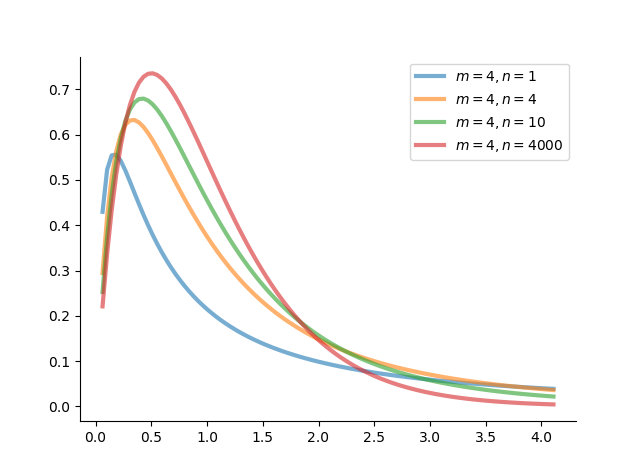
图 10：\(F\) 分布 \(F(m, n)\) 的概率密度图

---

\(t\) 分布

描述

设随机变量 \(X_1\) 与 \(X_2\) 独立且 \(X_1 \sim N(0,1)\)， \(X_2 \sim \mathcal{X}^2(n)\)，则称 \(t = \dfrac{X_1}{\sqrt{X_2 / n}}\) 的分布是自由度为 \(n\) 的 \(t\) 分布，记为 \(t \sim t(n)\)。由标准正态密度函数的对称性知，\(X_1\) 与 \(-X_1\) 有相同分布，从而 \(t\) 与 \(-t\) 有相同分布。其密度函数为
\begin{align}
p(y) = \dfrac{\Gamma\left(\dfrac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\dfrac{n}{2} \right)} \left( 1+ \dfrac{y^2}{n}\right)^{-\dfrac{n+1}{2}} , \qquad -\infty < y < +\infty
\end{align}

\(t\) 分布的密度函数的图像是一个关于纵轴对称的分布，与标准正态分布的密度函数形状类似，只是峰比标准正态分布低一些，尾部的概率比标准正态分布的大一些。且有以下结论：

• 自由度为 \(1\) 的 \(t\) 分布就是标准柯西分布，它的均值不存在
• \(n>1\) 时，\(t\) 分布的数学期望存在且为 \(0\)
• \(n>2\) 时，\(t\) 分布的方差存在，且为 \(\dfrac{n}{n-2}\)
• 当自由度较大（如 \(n\geqslant 30\) ）时，\(t\) 分布可以用 \(N(0,1)\) 分布近似

实验模拟

python 代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 22:36:31 2018

@author: zhoukui
"""

import matplotlib.pyplot as plt  
import numpy as np
from scipy.stats import t
from scipy.stats import norm

rv1 = t(1)
rv2 = t(2)
rv3 = t(4)
rv4 = norm()

# ppf: Percent point function 
x = np.linspace(rv4.ppf(0.001), rv4.ppf(0.999), 100)

fig = plt.figure()
ax = fig.add_subplot(111)

ax.spines['top'].set_visible(False)  # 设置线框不可见
ax.spines['right'].set_visible(False)

# pdf: Probability density function
ax.plot(x, rv1.pdf(x), lw = 3, alpha = 0.6, label = r'$t(1)$') 
ax.plot(x, rv2.pdf(x), lw = 3, alpha = 0.6, label = r'$t(2)$')
ax.plot(x, rv3.pdf(x), lw = 3, alpha = 0.6, label = r'$t(4)$')
ax.plot(x, rv4.pdf(x), lw = 3, alpha = 0.6, label = r'$N(0,1)$')

ax.legend()

# 可用 rvs 函数产生服从该分布的值
# 其中 loc 为平移量，从原先的 0~n 转变为 loc~loc+n   
#r = rv.rvs(size = 1000)

plt.show() 

结果如下图：

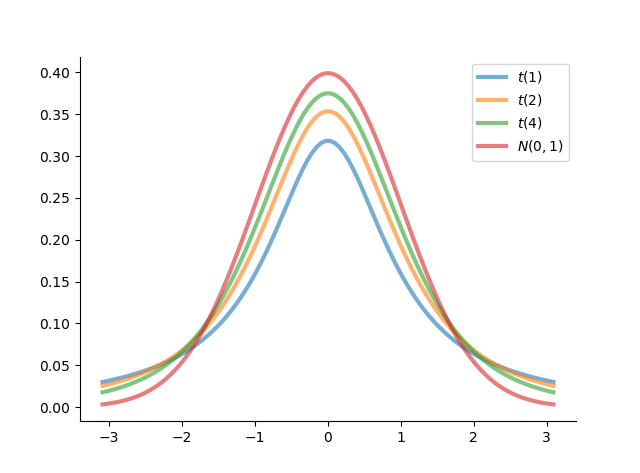
图 11：\(t\) 分布概率密度图