引言
对抗样本是深度学习模型的主要威胁之一,对抗样本会使得目标分类器模型分类出错并且它存在于稠密的对抗子空间中,对抗子空间又包含于特定的样本空间中。本文主要是对对抗子空间维数进行探讨,即针对于单个模型的特定样本对抗子空间的维度是多少,针对多个模型的特定样本对抗子空间的维度是多少。
对抗子空间
给定干净样本 x ∈ R d x\in \mathbb{R}^d x∈Rd,以及其对应的标签 y y y,带有参数 θ \theta θ的神经网络分类器为 f θ ( ⋅ ) f_\theta(\cdot) fθ(⋅),损失函数为 J ( x , y ; θ ) J(x,y;\theta) J(x,y;θ),对抗样本为 x ′ x^{\prime} x′,则根据多元泰勒展开式可得 J ( x ′ , y ; θ ) = J ( x , y ; θ ) + ( x ′ − x ) ⊤ ∇ x J ( x , y ; θ ) + O ( ∥ x ′ − x ∥ 2 ) J(x^{\prime},y;\theta)=J(x,y;\theta)+(x^{\prime}-x)^{\top}\nabla_x J(x,y;\theta)+O(\|x^{\prime}-x\|^2) J(x′,y;θ)=J(x,y;θ)+(x′−x)⊤∇xJ(x,y;θ)+O(∥x′−x∥2)进一步可得优化目标为 m a x i m i z e J ( x , y ; θ ) + ( x ′ − x ) ⊤ ∇ x J ( x , y ; θ ) s u b j e c t t o ∥ x ′ − x ∥ ∞ ≤ ε \begin{array}{rl}\mathrm{maximize}& J(x,y;\theta)+(x^{\prime}-x)^{\top}\nabla_x J(x,y;\theta)\\\mathrm{subject \text{ }to}& \|x^{\prime}-x\|_{\infty} \le \varepsilon\end{array} maximizesubject toJ(x,y;θ)+(x′−x)⊤∇xJ(x,y;θ)∥x′−x∥∞≤ε进而可得对抗样本的计算公式为 x ′ = x + ε ⋅ ∇ x J ( x , y ; θ ) x^{\prime}=x+\varepsilon \cdot\nabla_x J(x,y;\theta) x′=x+ε⋅∇xJ(x,y;θ)其中 ε \varepsilon ε表示的是对抗扰动的大小。由上公式可知,干净样本 x x x沿着梯度方向 ∇ x J ( x , y ; θ ) \nabla_x J(x,y;\theta) ∇xJ(x,y;θ)可以进入到对抗子空间中。进一步详细的阐述如下图所示,其中图(a),(b)和(c)表示的是给定一个干净样本沿着不同的方向生成的样本输入到分类器分类的结果示意图,每个方格表示每一个样本的分类结果,方格中白色表示分类器分类正确,彩色表示分类器分类成其它不同的类别。图(d) ,(e)和(f)表示样本移动的方向分解示意图。
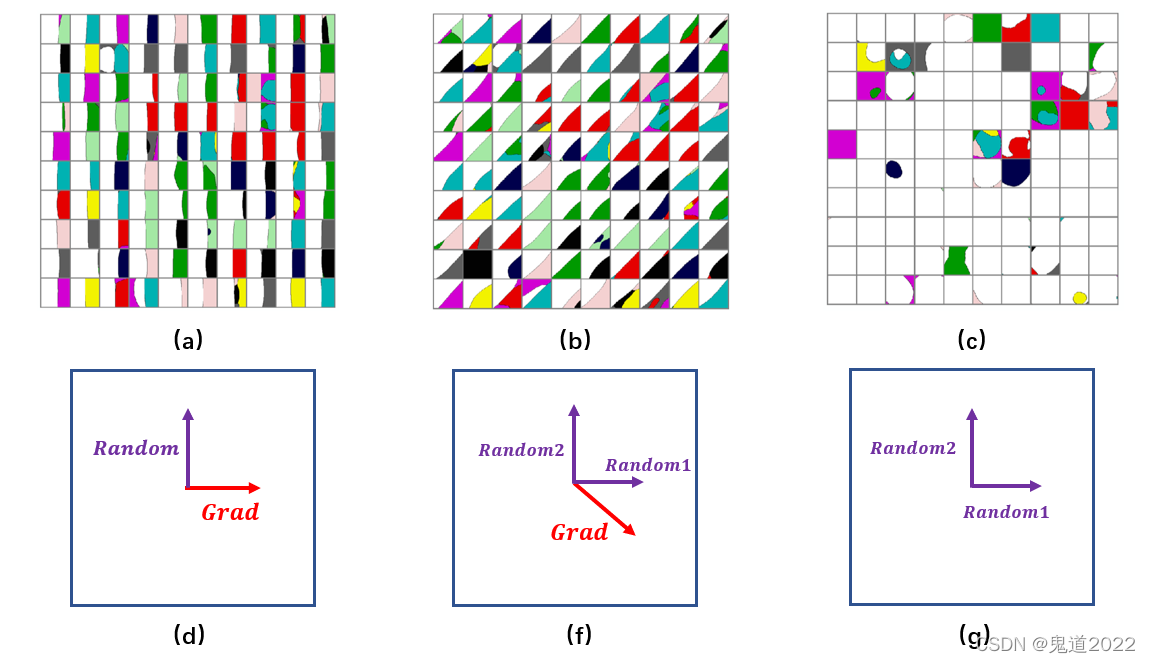
由上图(d)可知,如果选择两个正交方向,一个是对抗扰动的梯度方向,另一个是随机扰动方向,从图(a)可知,沿着对抗扰动方向的干净样本可以进入到对抗子空间中,沿着随机扰动的方向则没有生成对抗样本。由上图(e)可知,如果这两个正交方向与梯度方向成一个角度,则从图(b)可知这两个正交方向都可以进入到对抗子空间中,但是却不是最速方向。由上图(f)可知,如果这两个正交方向是都是随机扰动,从图(c)可知,干净样本都很难进入到对抗子空间中去,该图出现误分类的情况与对抗样本无关,跟模型自身的训练情况有关。
单模型对抗子空间维数
由上一节对对抗样本损失函数的多元泰勒展开可以近似有 J ( x ′ , y ; θ ) ≈ J ( x , y ′ ; θ ) + ( x ′ − x ) ⊤ ∇ x J ( x , y ; θ ) J(x^{\prime},y;\theta)\approx J(x,y';\theta)+(x^{\prime}-x)^{\top} \nabla_x J(x,y;\theta) J(x′,y;θ)≈J(x,y′;θ)+(x′−x)⊤∇xJ(x,y;θ)其中令 g = ∇ x J ( x , y ; θ ) ∈ R d g = \nabla_x J(x,y;\theta)\in \mathbb{R}^d g=∇xJ(x,y;θ)∈Rd, r = ( x ′ − x ) ∈ R d r = (x^{\prime}-x)\in \mathbb{R}^d r=(x′−x)∈Rd。目的是要探究给定一个模型,求解对抗扰动 r r r使得模型损失函数至少增长 α \alpha α得对抗子空间维度的问题,数学表述为 J ( x ′ , y ; θ ) − J ( x , y ; θ ) = r ⊤ g ≥ α \begin{aligned}J(x^{\prime},y;\theta)-J(x,y;\theta)&=r^{\top} g\ge \alpha\\\end{aligned} J(x′,y;θ)−J(x,y;θ)=r⊤g≥α其中 r ∈ S p a n { r 1 , r 2 ⋯ , r k } r \in \mathrm{Span}\{r_1,r_2\cdots,r_k\} r∈Span{ r1,r2⋯,rk},即扰动 r r r属于 r 1 , r 2 , ⋯ , r k r_1,r_2,\cdots,r_k r1,r2,⋯,rk这 k k k个正交向量组成的对抗子空间中, k k k就是对抗子空间的维度。此时有如下定理成立,详细证明过程如下所示:
定理: 给定 g ∈ R d g \in \mathbb{R}^{d} g∈Rd 和 α ∈ [ 0 , 1 ] \alpha \in[0,1] α∈[0,1],最大对抗子空间维数 k k k的正交向量 r 1 , r 2 , … , r k r_1,r_2,\ldots,r_k r1,r2,…,rk 满足 ∥ r i ∥ 2 ≤ 1 \left\|r_{i}\right\|_{2} \leq 1 ∥ri∥2≤1, g ⊤ r i ≥ α ⋅ ∥ g ∥ 2 g^{\top} r_{i} \geq \alpha \cdot\|g\|_{2} g⊤ri≥α⋅∥g∥2的充要条件是 k = min { ⌊ 1 α 2 ⌋ , d } k=\min \left\{\left\lfloor\frac{1}{\alpha^{2}}\right\rfloor, d\right\} k=min{ ⌊α21⌋,d}。
证明:
必要性证明: 已知 g ∈ R d g \in \mathbb{R}^{d} g∈Rd 和 α ∈ [ 0 , 1 ] \alpha \in[0,1] α∈[0,1],令 r ^ i : = r i ∥ r i ∥ 2 \hat{r}_{i}:=\frac{r_{i}}{\left\|r_{i}\right\|_{2}} r^i:=∥ri∥2ri,并且 r 1 , r 2 , … , r k r_{1}, r_{2}, \ldots, r_{k} r1,r2,…,rk是正交的,由此可知 k ≤ d k \leq d k≤d。
(1)如果 k = d k = d k=d,则由向量乘积公式可知: ∑ i = 1 k ∣ g ⊤ r ^ i ∣ 2 = ∑ i = 1 d ∣ g ⊤ r ^ i ∣ 2 = ∑ i = 1 d ∥ g ∥ 2 2 ∥ r ^ i ∥ 2 2 cos 2 α i \sum_{i=1}^{k}\left|g^{\top} \hat{r}_{i}\right|^{2}=\sum_{i=1}^{d}\left|g^{\top} \hat{r}_{i}\right|^{2} = \sum_{i=1}^{d} \|g\|_{2}^{2} \|\hat{r}_{i}\|_{2}^{2} \cos^{2} \alpha_{i} i=1∑k∣∣g⊤r^i∣∣2=i=1∑d∣∣g⊤r^i∣∣2=i=1∑d∥g∥22∥r^i∥22cos2αi其中, cos α i \cos \alpha_{i} cosαi 表示的是向量 g g g和 r ^ i \hat{r}_{i} r^i的余弦值,并且又知道 ∥ r ^ i ∥ 2 2 = 1 \|\hat{r}_{i}\|_{2}^{2}=1 ∥r^i∥22=1,所以有 ∑ i = 1 d ∥ g ∥ 2 2 ∥ r ^ i ∥ 2 2 cos 2 α i = ∥ g ∥ 2 2 ∑ i = 1 d cos 2 α i = ∥ g ∥ 2 2 \sum_{i=1}^{d} \|g\|_{2}^{2} \|\hat{r}_{i}\|_{2}^{2} \cos^{2} \alpha_{i} = \|g\|_{2}^{2} \sum_{i=1}^{d} \cos^{2} \alpha_{i} = \|g\|_{2}^{2} i=1∑d∥g∥22∥r^i∥22cos2αi=∥g∥22i=1∑dcos2αi=∥g∥22进而则有 ∑ i = 1 k ∣ g ⊤ r ^ i ∣ 2 = ∥ g ∥ 2 2 \sum_{i=1}^{k}\left|g^{\top} \hat{r}_{i}\right|^{2} = \|g\|_{2}^{2} i=1∑k∣∣g⊤r^i∣∣2=∥g∥22
(2)如果 k < d k < d k<d,则先对 r 1 , r 2 , … , r k r_{1}, r_{2}, \ldots, r_{k} r1,r2,…,rk进行正交扩充,扩充为 r 1 , r 2 , … , r k , r k + 1 , … , r d r_{1}, r_{2}, \ldots, r_{k}, r_{k+1},\ldots, r_{d} r1,r2,…,rk,rk+1,…,rd则可知 ∑ i = 1 k ∣ g ⊤ r ^ i ∣ 2 < ∑ i = 1 d ∣ g ⊤ r ^ i ∣ 2 = ∑ i = 1 d ∥ g ∥ 2 2 ∥ r ^ i ∥ 2 2 cos 2 α i = ∥ g ∥ 2 2 \sum_{i=1}^{k}\left|g^{\top} \hat{r}_{i}\right|^{2}< \sum_{i=1}^{d}\left|g^{\top} \hat{r}_{i}\right|^{2} = \sum_{i=1}^{d} \|g\|_{2}^{2} \|\hat{r}_{i}\|_{2}^{2} \cos^{2} \alpha_{i} = \|g\|_{2}^{2} i=1∑k∣∣g⊤r^i∣∣2<i=1∑d∣∣g⊤r^i∣∣2=i=1∑d∥g∥22∥r^i∥22cos2αi=∥g∥22进而可知 ∥ g ∥ 2 2 ≥ ∑ i = 1 k ∣ g ⊤ r ^ i ∣ 2 \|g\|_{2}^{2} \geq \sum_{i=1}^{k}\left|g^{\top} \hat{r}_{i}\right|^{2} ∥g∥22≥i=1∑k∣∣g⊤r^i∣∣2又因为 r ^ i : = r i ∥ r i ∥ 2 \hat{r}_{i}:=\frac{r_{i}}{\left\|r_{i}\right\|_{2}} r^i:=∥ri∥2ri,所以有 ∑ i = 1 k ∣ g ⊤ r ^ i ∣ 2 = ∑ i = 1 k ∣ g ⊤ r i ∥ r i ∥ 2 ∣ 2 ≥ ∑ i = 1 k ∣ g ⊤ r i ∣ 2 ∥ r i ∥ 2 2 \sum_{i=1}^{k}\left|g^{\top} \hat{r}_{i}\right|^{2} = \sum_{i=1}^{k}\left|g^{\top} \frac{r_{i}}{\left\|r_{i}\right\|_{2}} \right|^{2} \geq \sum_{i=1}^{k} \frac{\left|g^{\top} r_{i}\right|^{2}}{\left\|r_{i}\right\|_{2}^{2}} i=1∑k∣∣g⊤r^i∣∣2=i=1∑k∣∣∣∣g⊤∥ri∥2ri∣∣∣∣2≥i=1∑k∥ri∥22∣∣g⊤ri∣∣2
因为 g ⊤ r i ≥ α ⋅ ∥ g ∥ 2 g^{\top} r_{i} \geq \alpha \cdot\|g\|_{2} g⊤ri≥α⋅∥g∥2, ∥ r i ∥ 2 ≤ 1 \left\|r_{i}\right\|_{2} \leq 1 ∥ri∥2≤1,所以有 ∑ i = 1 k ∣ g ⊤ r i ∣ 2 ∥ r i ∥ 2 2 ≥ k ⋅ α 2 ⋅ ∥ g ∥ 2 2 \sum_{i=1}^{k} \frac{\left|g^{\top} r_{i}\right|^{2}}{\left\|r_{i}\right\|_{2}^{2}} \geq k \cdot \alpha^{2} \cdot\|g\|_{2}^{2} i=1∑k∥ri∥22∣∣g⊤ri∣∣2≥k⋅α2⋅∥g∥22又因为 k ≤ ⌊ 1 α 2 ⌋ k \leq \left\lfloor\frac{1}{\alpha^{2}}\right\rfloor k≤⌊α21⌋
最终有 max { k } = min { ⌊ 1 α 2 ⌋ , d } \max\{k\} = \min\{ \left\lfloor\frac{1}{\alpha^{2}}\right\rfloor,d\} max{
k}=min{
⌊α21⌋,d}
充分性证明: 已知 k = min { ⌊ 1 α 2 ⌋ , d } k=\min \left\{\left\lfloor\frac{1}{\alpha^{2}}\right\rfloor, d\right\} k=min{
⌊α21⌋,d},令 e 1 , e 2 , … , e d e_{1}, e_{2}, \dots, e_{d} e1,e2,…,ed表示的是 R d \mathbb{R}_{d} Rd的基向量, R R R为旋转矩阵并且有 R g = ∥ g ∥ 2 ⋅ e 1 R g=\|g\|_{2} \cdot e_{1} Rg=∥g∥2⋅e1。 令 z : = ∑ i = 1 k k − 1 2 ⋅ e i z:=\sum_{i=1}^{k} k^{-\frac{1}{2}} \cdot e_{i} z:=∑i=1kk−21⋅ei,并且 S S S为旋转矩阵,所以有 S z = ∥ z ∥ 2 e 1 = e 1 S z=\|z\|_{2} e_{1}= e_{1} Sz=∥z∥2e1=e1
易知,矩阵 Q : = S ⊤ R Q:=S^{\top} R Q:=S⊤R为旋转矩阵,其满足 Q g = S ⊤ R g = ∥ g ∥ 2 S ⊤ e 1 = ∥ g ∥ 2 z Q g= S^{\top} R g = \|g\|_{2} S^{\top} e_1 = \|g\|_{2} z Qg=S⊤Rg=∥g∥2S⊤e1=∥g∥2z
令向量 r i : = Q ⊤ e i r_{i}:=Q^{\top} e_{i} ri:=Q⊤ei,并且 1 ≤ i ≤ k 1 \leq i \leq k 1≤i≤k ,其中 r i r_i ri是矩阵 Q Q Q的第 i i i列, Q Q Q是正交矩阵,进而可知: g ⊤ r i = ( Q g ) ⊤ e i = ∥ g ∥ 2 ⋅ z ⊤ e i = ∥ g ∥ 2 ⋅ k − 1 2 ≥ ∥ g ∥ 2 ⋅ α g^{\top} r_{i}=(Qg)^{\top}e_{i} = \|g\|_{2} \cdot z^{\top} e_{i}=\|g\|_{2} \cdot k^{-\frac{1}{2}} \geq\|g\|_{2} \cdot \alpha g⊤ri=(Qg)⊤ei=∥g∥2⋅z⊤ei=∥g∥2⋅k−21≥∥g∥2⋅α
证毕!
通过以上的证明可以得到一个非常严谨漂亮的结论,即对抗子空间的维度 k k k大小与损失函数增长程度 α \alpha α的平方成反比,这也是很符合直观理解。增长程度越大,对抗子空间就越往梯度方向坍缩,因为梯度方向是最速方向。
多模型对抗子空间维数
在黑盒模型中,经常会利用到对抗样本的可迁移性进行攻击,即利用模型 f θ f_{\theta} fθ生成的对抗样本 x ′ x^{\prime} x′,迁移未知分类模型 g η g_\eta gη中进行攻击,其主要原因在于针对两个不同的模型有重叠的对抗子空间,所以才会使得对抗样本有攻击的可迁移性。假定 r r r表示的是样本 x x x针对模型 f θ f_\theta fθ的使得其损失函数增长 α \alpha α的对抗扰动; s s s表示的是样本 x x x针对模型 g η g_\eta gη的使得其损失函数增长 α \alpha α的对抗扰动。其中 r ∈ S p a n { r 1 , r 2 ⋯ , r k } r \in \mathrm{Span}\{r_1,r_2\cdots,r_k\} r∈Span{ r1,r2⋯,rk},即扰动 r r r属于 r 1 , r 2 , ⋯ , r k r_1,r_2,\cdots,r_k r1,r2,⋯,rk这 k k k个正交向量组成的对抗子空间中。其中 s ∈ S p a n { s 1 , s 2 ⋯ , s l } s \in \mathrm{Span}\{s_1,s_2\cdots,s_l\} s∈Span{ s1,s2⋯,sl},即扰动 s s s属于 s 1 , s 2 , ⋯ , s l s_1,s_2,\cdots,s_l s1,s2,⋯,sl这 l l l个正交向量组成的对抗子空间中;则此时针对多个模型对抗子空间维度的大小为 q = d i m { S p a n { r 1 , r 2 , ⋯ , r k } ⋂ S p a n { s 1 , s 2 , ⋯ , s l } } q=\mathrm{dim}\{\mathrm{Span}\{r_1,r_2,\cdots,r_k\}\bigcap\mathrm{Span}\{s_1,s_2,\cdots,s_l\}\} q=dim{ Span{ r1,r2,⋯,rk}⋂Span{ s1,s2,⋯,sl}}同理根据以上推导思路可以求出3个模型以上重叠的对抗子空间的维度。