多重信号分类MUSIC算法
1. MUSIC算法原理
MUSIC算法,叫做多信号分类算法 (Multiple Signal classification),是一种基于特征结构的高分辨率DOA算法。该算法利用了信号子空间和噪声子空间正交性的特点,构造噪声空间然后通过谱峰搜索来检测信号的波达方向。需要注意的是,该算法有一个前提,即各个入射信号之间互不相关,这样才能保证入射信号的协方差矩阵是满秩的。
考虑以下这个线阵模型:
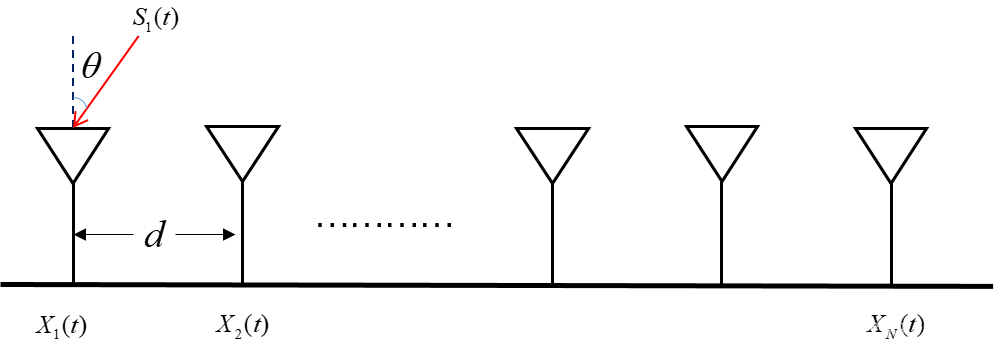
令 X ( t ) X(t) X(t) 是在第 t t t 个快拍观察到的数据向量。在阵列信号处理和空间谱估计中, X ( t ) = \boldsymbol{X}(t)= X(t)= [ X 1 ( t ) , X 2 ( t ) , ⋯ , X N ( t ) ] T \left[X_{1}(t), X_{2}(t), \cdots, X_{N}(t)\right]^{\mathrm{T}} [X1(t),X2(t),⋯,XN(t)]T 由 n n n 个阵元 (天线或传感器) 的观测数据组成。在时域谱估计中,向量 x ( t ) = [ x ( t ) , x ( t − 1 ) , ⋯ , x ( t − n − 1 ) ] T \boldsymbol{x}(t)=[x(t), x(t-1), \cdots, x(t-n-1)]^{\mathrm{T}} x(t)=[x(t),x(t−1),⋯,x(t−n−1)]T 由连续的 n n n 个观察数据样本组成。
假定数据向量 X ( t ) \boldsymbol{X}(t) X(t) 是 r r r 个窄带信号入射到 N N N 个阵元组成的阵列的观察数据向量或者是 r r r 个不相干的复谐波的叠加,即
X ( t ) = ∑ i = 1 r s i ( t ) a ( ω i ) + v ( t ) = A s ( t ) + n ( t ) \boldsymbol{X}(t)=\sum_{i=1}^{r} s_{i}(t) \boldsymbol{a}\left(\omega_{i}\right)+\boldsymbol{v}(t)=\boldsymbol{A} \boldsymbol{s}(t)+\boldsymbol{n}(t) X(t)=i=1∑rsi(t)a(ωi)+v(t)=As(t)+n(t)式中, A = [ a ( ω 1 ) , ⋯ , a ( ω r ) ] \boldsymbol{A}=\left[\boldsymbol{a}\left(\omega_{1}\right), \cdots, \boldsymbol{a}\left(\omega_{r}\right)\right] A=[a(ω1),⋯,a(ωr)] 为 N × r N \times r N×r 阵列流型矩阵, a ( ω i ) = [ 1 , e j ω i , … , e j ( N − 1 ) ω i ] T \boldsymbol{a}\left(\omega_{i}\right)=\left[1, \mathrm{e}^{\mathrm{j} \omega_{i}}, \ldots, \mathrm{e}^{\mathrm{j}(N-1) \omega_{i}}\right]^{\mathrm{T}} a(ωi)=[1,ejωi,…,ej(N−1)ωi]T 为方向向量; s ( t ) = [ s 1 ( t ) , ⋯ , s r ( t ) ] T \boldsymbol{s}(t)=\left[s_{1}(t), \cdots, s_{r}(t)\right]^{\mathrm{T}} s(t)=[s1(t),⋯,sr(t)]T 为随机信号向量,其均值为零向量,协方差矩阵为 R s = E { s ( t ) s H ( t ) } ; \boldsymbol{R}_{\boldsymbol{s}}=\mathrm{E}\left\{\boldsymbol{s}(t) \boldsymbol{s}^{\mathrm{H}}(t)\right\} ; Rs=E{
s(t)sH(t)}; 而 v ( t ) = [ v 1 ( t ) , ⋯ , v N ( t ) ] T \boldsymbol{v}(t)=\left[v_{1}(t), \cdots, v_{N}(t)\right]^{\mathrm{T}} v(t)=[v1(t),⋯,vN(t)]T 为加性噪声向量,其各个分量为高斯白噪声,它们具有零均值和相同的方差 σ 2 \sigma^{2} σ2 。在谐波恢复中,参数 ω i \omega_{i} ωi 为复谐波的 频率 ; 在阵列信号处理中, ω i \omega_{i} ωi 是一空间参数
ω i = 2 π d λ sin θ i \omega_{i}=2 \pi \frac{d}{\lambda} \sin \theta_{i} ωi=2πλdsinθi式中, d d d 为相邻两个阵元之间的距离 (假定阵元等间距排列成一直线), λ \lambda λ 为波长, 且 θ i \theta_{i} θi 表 示第 i i i 个窄带信号达到阵元的入射方向,简称波达方向。
MUSIC算法要解决的是根据 N N N 个快拍的观测数据向量 X ( t ) ( t = 1 , 2 , ⋯ , N ) \boldsymbol{X}(t)(t=1,2, \cdots, N) X(t)(t=1,2,⋯,N) 估计 r r r 个参数 ω i ∘ \omega_{i \circ} ωi∘ 这相当于对 r r r 个混合信号进行分类,简称多重信号分类。
假定噪声向量 v ( t ) \boldsymbol{v}(t) v(t) 与信号向量 s ( t ) \boldsymbol{s}(t) s(t) 统计不相关,并令观测数据向量的协方差矩阵 R x x = E { x ( t ) x H ( t ) } \boldsymbol{R}_{x x}=\mathrm{E}\left\{\boldsymbol{x}(t) \boldsymbol{x}^{\mathrm{H}}(t)\right\} Rxx=E{
x(t)xH(t)} 的特征值分解为
R x x = A R s s A H + σ 2 I = U Σ U H = [ U S , U N ] [ Σ S O O Σ N ] [ U S H U N H ] \boldsymbol{R}_{x x}=\boldsymbol{A R}_{s s} \boldsymbol{A}^{\mathrm{H}}+\sigma^{2} \boldsymbol{I}=\boldsymbol{U} \boldsymbol{\Sigma} \boldsymbol{U}^{\mathrm{H}}=[\boldsymbol{U_S}, \boldsymbol{U_N}]\left[\begin{array}{cc} \boldsymbol{\Sigma_S} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{\Sigma_N} \end{array}\right]\left[\begin{array}{l} \boldsymbol{U}^{\mathrm{H}}_S \\ \boldsymbol{U}^{\mathrm{H}}_N \end{array}\right] Rxx=ARssAH+σ2I=UΣUH=[US,UN][ΣSOOΣN][USHUNH]式中, R s s = E { s ( t ) s H ( t ) } , \boldsymbol{R}_{s s}=\mathrm{E}\left\{\boldsymbol{s}(t) \boldsymbol{s}^{\mathrm{H}}(t)\right\}, Rss=E{
s(t)sH(t)}, 且 Σ S \boldsymbol{\Sigma_S} ΣS 包含了 r r r 个大特征值, 它们比 σ 2 \sigma^{2} σ2 明显大很多, Σ N = σ 2 I n − r \boldsymbol{\Sigma_N}=\sigma^{2} I_{n-r} ΣN=σ2In−r。
因此有:
R x x U N = [ U S , U N ] [ Σ S O O Σ N ] [ U S H U N H ] U N = [ U S , U N ] [ Σ S O O Σ N ] [ O I ] = σ 2 U N \boldsymbol{R}_{x x} \boldsymbol{U_N}=[\boldsymbol{U_S}, \boldsymbol{U_N}]\left[\begin{array}{cc} \boldsymbol{\Sigma_S} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{\Sigma_N} \end{array}\right]\left[\begin{array}{l} \boldsymbol{U}^{\mathrm{H}}_S \\ \boldsymbol{U}^{\mathrm{H}}_N \end{array}\right]\boldsymbol{U_N}=[\boldsymbol{U_S}, \boldsymbol{U_N}]\left[\begin{array}{cc}\boldsymbol{\Sigma_S} & \boldsymbol{O} \\ \boldsymbol{O} & \boldsymbol{\Sigma_N}\end{array}\right]\left[\begin{array}{l}\boldsymbol{O} \\ \boldsymbol{I}\end{array}\right]=\sigma^{2} \boldsymbol{U_N} RxxUN=[US,UN][ΣSOOΣN][USHUNH]UN=[US,UN][ΣSOOΣN][OI]=σ2UN
又由 R x x = A R s s A H + σ 2 I \boldsymbol{R}_{x x}=\boldsymbol{A R}_{s s} \boldsymbol{A}^{\mathrm{H}}+\sigma^{2} \boldsymbol{I} Rxx=ARssAH+σ2I 有 R x x U N = A R s s A H U N + σ 2 U N , \boldsymbol{R}_{x x} \boldsymbol{U_N}=\boldsymbol{A R}_{s s} \boldsymbol{A}^{\mathrm{H}} \boldsymbol{U_N}+\sigma^{2} \boldsymbol{U_N}, RxxUN=ARssAHUN+σ2UN,联立上式可以得到
A R s s A H U N = O \boldsymbol{A R}_{s s} \boldsymbol{A}^{\mathrm{H}} \boldsymbol{U_N}=\boldsymbol{O} ARssAHUN=O进而有
U N H A R s s A H U N = O \boldsymbol{U}^{\mathrm{H}}_N \boldsymbol{A R}_{s s} \boldsymbol{A}^{\mathrm{H}} \boldsymbol{U_N}=\boldsymbol{O} UNHARssAHUN=O
众所周知, Q \boldsymbol{Q} Q 非奇异时 t H Q t = 0 , \boldsymbol{t}^{\mathrm{H}} \boldsymbol{Q} \boldsymbol{t}=0, tHQt=0, 当且仅当 t = 0 , \boldsymbol{t}=\mathbf{0}, t=0, 故上式成立的充分必要条件是
A H U N = O \boldsymbol{A}^{\mathrm{H}} \boldsymbol{U_N}=\boldsymbol{O} AHUN=O因为 R s s = E { s ( t ) s H ( t ) } R_{s s}=\mathrm{E}\left\{s(t) s^{\mathrm{H}}(t)\right\} Rss=E{
s(t)sH(t)} 非奇异。将 A = [ a ( ω 1 ) , ⋯ , a ( ω p ) ] \boldsymbol{A}=\left[\boldsymbol{a}\left(\omega_{1}\right), \cdots, \boldsymbol{a}\left(\omega_{p}\right)\right] A=[a(ω1),⋯,a(ωp)] 代入上式即有
a H ( ω ) G = 0 T , ω = ω 1 , ω 2 , ⋯ , ω p \boldsymbol{a}^{\mathrm{H}}(\omega) \boldsymbol{G}=\mathbf{0}^{\mathrm{T}}, \quad \omega=\omega_{1}, \omega_{2}, \cdots, \omega_{p} aH(ω)G=0T,ω=ω1,ω2,⋯,ωp显然, 当 ω ≠ ω 1 , ω 2 , ⋯ , ω p \omega \neq \omega_{1}, \omega_{2}, \cdots, \omega_{p} ω=ω1,ω2,⋯,ωp 时, a H ( ω ) G ≠ 0 T \boldsymbol{a}^{\mathrm{H}}(\omega) \boldsymbol{G} \neq \mathbf{0}^{\mathrm{T}} aH(ω)G=0T 。
将上式改写成标量形式, 可以定义一种类似于功率谱的函数
P ( ω ) = 1 a H ( ω ) U N U N H a ( ω ) \boldsymbol P(\omega)=\frac{1}{\boldsymbol a^{\mathrm{H}}(\omega) \boldsymbol U_N \boldsymbol U^{\mathrm{H}}_N \boldsymbol a(\omega)} P(ω)=aH(ω)UNUNHa(ω)1由于噪声的影响, a H ( ω ) U N U N H a ( ω ) ≠ 0 \boldsymbol{a}^{\mathrm{H}}(\omega) \boldsymbol{U_N} \boldsymbol{U}^{\mathrm{H}}_N \boldsymbol{a}(\omega)\neq0 aH(ω)UNUNHa(ω)=0,而是一个很小的数,因此此时的 P ( ω ) \boldsymbol P(\omega) P(ω)是一个极大值。对上式取峰值的 r r r 个 ω \omega ω 值 ω 1 , ω 2 , ⋯ , ω r \omega_{1}, \omega_{2}, \cdots, \omega_{r} ω1,ω2,⋯,ωr 给出 r r r 个信号的波达方向 θ 1 , θ 2 , ⋯ , θ r \theta_{1}, \theta_{2}, \cdots, \theta_{r} θ1,θ2,⋯,θr。
同时在实际应用中,接收阵接收到的数据有限长,我们可以通过这些数据估计入射信号的协方差矩阵,达到极大似然估计的目的。假设有M个快拍snapshot,则有
R ^ x x = 1 M ∑ i = 1 M x i x i H \hat{R}_{xx}=\frac{1}{M} \sum_{i=1}^{M} x_{i} x_{i}^{H} R^xx=M1i=1∑MxixiH然后对协方差矩阵 R ^ x x \hat{R}_{xx} R^xx进行特征值分解:
R ^ x x = U Σ U H \begin{aligned} \hat{R}_{xx} &={U} \Sigma{U}^{H} \end{aligned} R^xx=UΣUH特征值分解后按照特征值的大小(从大到小)对特征向量进行重排,接下来就是要确定噪声子空间。假设排序后的特征值 σ 1 2 ⩾ σ 2 2 ⩾ ⋯ ⩾ σ r 2 ⩾ σ r + 1 2 ⩾ ⋯ ⩾ σ N 2 \sigma_{1}^{2} \geqslant \sigma_{2}^{2} \geqslant \cdots \geqslant \sigma_{r}^{2} \geqslant \sigma_{r+1}^{2}\geqslant \cdots \geqslant \sigma_{N}^{2} σ12⩾σ22⩾⋯⩾σr2⩾σr+12⩾⋯⩾σN2,接收信号总能量定义为 P = σ 1 2 + σ 2 2 + ⋯ + σ N 2 P=\sigma_{1}^{2}+\sigma_{2}^{2}+\cdots+\sigma_{N}^{2} P=σ12+σ22+⋯+σN2根据能量准则,如果J是满足下式的最小整数: σ 1 2 + σ 2 2 + ⋯ + σ J 2 P ⩾ 0.95 或 0.9 \frac{\sigma_{1}^{2}+\sigma_{2}^{2}+\cdots+\sigma_{J}^{2}}{P}\geqslant0.95或0.9 Pσ12+σ22+⋯+σJ2⩾0.95或0.9那么 { σ J + 1 2 , σ J + 2 2 ⋯ , σ N 2 } \{\sigma_{J+1}^{2},\sigma_{J+2}^{2}\cdots,\sigma_{N}^{2}\} {
σJ+12,σJ+22⋯,σN2}对应的特征向量组成的空间 U N ^ \hat{U_N} UN^即为噪声子空间。
还有另外一种确定J的方法,即J是满足下式的最小整数:
σ J 2 σ J + 1 2 ⩾ 10 \frac{\sigma_{J}^{2}}{\sigma_{J+1}^{2}}\geqslant10 σJ+12σJ2⩾10
然后就可以用 P ( ω ) = 1 a H ( ω ) U ^ N U ^ N H a ( ω ) \boldsymbol P(\omega)=\frac{1}{\boldsymbol a^{\mathrm{H}}(\omega) \boldsymbol {\hat U_N} \boldsymbol {\hat U^{\mathrm{H}}_N} \boldsymbol a(\omega)} P(ω)=aH(ω)U^NU^NHa(ω)1进行谱峰搜索,寻找r个入射信号的来波方向。