主成分分析PCA和核化线性降维kernel PCA

一、前言

主成分分析（Principal Component Analysis）是最常用的一种降维方法。以前经常用PCA用来特征的降维，但对原理和实现方法理解的不透彻，用起来心里没底，这几天有空总结一下PCA的原理。

二、原理

在正交属性空间中的样本点，如何使用一个超平面对所有样本进行恰当的表达？这样的超平面应该有这样的性质：

• 最近重构性：样本点到这个超平面的距离足够近（尽量少的信息损失）
• 最大可分性：样本点到这个超平面的投影能尽可能分开

有趣的是基于最近重构性和最大可分性，能分别得到主成分分析的两种等价的推导。首先从最近重构性来推导：
假定数据样本进行了中心化，即$\sum_{i=1}^nx_i=0$；投影变换后的新坐标系为{ $\omega_1,\omega_2, ..., \omega_d$}，其中$\omega_i$是标准正交基向量，$\left|\left|\omega_i\right|\right|_2=1$，$\omega_i^T\omega_j=0,(i\neq j)$。当丢弃新坐标系中的部分坐标，即将维度降低到$d'$，则样本点$x_i$在低维坐标系中的投影是$z_i=(z_{i1},z_{i2}, ..., z_{id'})$，其中$z_{ij}=\omega_j^Tx_i$是$x_i$在低维坐标系下第j维的坐标。若基于$z_i$来重构$x_i$，则会得到$\hat{x}_i=\sum_{j=1}^{d'}z_{ij}\omega_j$.
对于整个训练集，原样本点$x_i$与基于投影重建的样本点$\hat{x}_i$之间的距离为：

$$\sum_{i=1}^m\left|\left|\sum_{j=1}^d'z_{ij}\omega_j-x_i\right|\right|_2^2=\sum_{i=1}^mz_i^Tz_i-2\sum_{i=1}^mz_i^TW^ Tx_i+const$$
$$\propto-tr(W^T(\sum_{i=1}^mx_ix_i^T)W).$$
其中const是个常数，根据最近重构性，上式应该被最小化，有：
$$min_W -tr(W^TXX^TW)$$
$$s.t. W^TW=I$$
这就是主成分分析的优化目标。
从最大可分性推导，能得到主成分分析的另一种解释，样本点 $x_i$在新空间中超平面上的投影是W^Tx_i，要想达到最大可分性，就应该使投影后样本的方差最大化，于是优化目标可写为：
$$max _W tr(W^TXX^TW)$$
$$s.t. W^TW=I$$
显然从最大可分性出发和从最近重构性出发得到的优化目标是一样的，对其使用拉格朗日乘子法可得：
$$XX^TW=\lambda W$$
于是，只需对协方差矩阵 $XX^T$进行特征值分解，将求得的特征值排序，再取前 $d'$个特征值对应的特征向量构成 $W=(w_1, w_2, ..., w_d')$.这就是主成分分析的解.
白话总结，将一组N维向量降为K维（K大于0，小于N），其目标是选择K个单位（模为1）正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，而字段的方差则尽可能大（在正交的约束下，取最大的K个方差）。
PCA本质上就是把方差最大的方向作为主要特征，并且在各个正交方向上将数据“离相关”，也就是让它们在不同正交方向上没有相关性。

三、算法

输入：样本集D={ $x_1$,$x_2$, … ,$x_n$}；低纬空间维数d
过程：
-1. 对所有所有样本进行中心化$x_i$=$x_i$ - $\frac{1}{m}$$\sum_{i=1}^m(x_i)$
-2. 计算样本的协方差矩阵$X\ast X^T$
-3. 对协方差矩阵做特征值分解
-4. 选出最大的d个特征值所对应的特征向量$\omega_1,\omega_2, ..., \omega_d$
输出：投影矩阵$W=(\omega_1,\omega_2, ..., \omega_d)$
降维之后低维空间的维度$d'$通常是由用户指定的，或通过在$d'$值不同的低纬空间中对k近邻分类器（或其他开销较小的分类器）进行交叉验证来选取。对PCA，还可以从重构的角度设置一个重构阈值，例如取$t=95%$，然后选取使下式成立的$d'$:

$$\frac{\sum_{i=1}^{d'}\lambda_i}{\sum_{i=1}^{d}\lambda_i}\geq t$$

四、PCA实例

五、核主成分分析KPCA

PCA存在一些限制，例如它可以很好的解除线性相关，但是对于高阶相关性就没有办法了，对于存在高阶相关性的数据，可以考虑Kernel PCA，通过Kernel函数将非线性相关转为线性相关。
非线性降维的一种常用方法，是基于核技巧对线性降维方法进行核化，下面介绍核主成分分析（Kernelized PCA）的实现原理。
假定，我们将在高维空间中把数据投影到由$W$确定的超平面上，即PCA欲求解

$$(\sum_{i=1}^mz_iz_i^T)W=\lambda W\tag{1}$$
其中 $z_i$样本点 $x_i$在高维特征空间中的像，则

$$W=\frac{1}{m}(\sum_{i=1}^mz_iz_i^T)W=\sum_{i=1}^mz_i\frac{z_i^TW}{\lambda}=\sum_{i=1}^mz_i\alpha_i\tag{2}$$
其中 $\alpha_i=\frac{1}{\lambda}z_i^TW$.假定 $z_i$是由原始属性空间中的样本点 $x_i$通过映射 $\phi$产生，即 $z_i=\phi(x_i), i=1,2,...,m$。若 $\phi$能被显式表达出来，则通过它将样本映射到高维特征空间，再在特征空间中实施PCA即可，上面两式变为：
$$\left( \sum_{i=1}^m\phi(x_i)\phi(x_i)^T \right)W=\lambda W \tag{3}$$
$$W=\sum_{i=1}^m\phi(x_i)\alpha_i\tag{4}$$ .
一般情况下，我们不清楚 $\phi$的具体形式，于是引入核函数
$$k(x_i,x_j)=\phi(x_i)^T\phi(x_j)\tag{5}$$
将4、5式带入3式化简可得：
$$KA=\lambda A\tag{6}$$
其中， $K$为 $k$对应的核矩阵， $(K)_{ij}=k(x_i,x_j)$, $A=(\alpha_1,\alpha_2,...,\alpha_n)$. 取 $K$最大的 $d'$个特征值对应的特征向量即可。
对新样本 $x$,其投影后第 $j(j=1,2,...,d')$维坐标为：
$$z_j=w_j^T\phi(x)=\sum_{i=1}^m\alpha_j^j\phi(x_i)^T\phi(x)=\sum_{i=1}^m\alpha_j^jk(x_i,x_j)\tag{7}$$
其中 $\alpha_i$已经规范化， $\alpha_i^j$是 $\alpha_i$的第j个分量。由式7可以看出，KPCA需要对所有样本求和，因此它的计算开销较大。

常用的核函数：

多项式核：

$$k(x^i,x^j)=((x^i)^Tx^j-\Theta)$$
径向基核函数(RBF)(高斯核函数)：
$$k(x^i,x^j)=exp(-\frac{|| x^i-x^j ||^2}{2\sigma^2})$$

六、sklearn中PCA的使用方法

函数原型及参数说明

sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)
n_conmponents:保留的特征个数，缺省为none，保留所有特征；“mle”表示使用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维；当去(0,1)之间的小数时，表示从重构的角度设置一个重构阈值，选取合适的特征数；
copy:是否改变元数据，默认为True
whiten:是否进行白化处理，缺省值为False，白化的概念参看Ufldl教程
输出：
pca.explained_variance_ratio_ ：投影后的特征维度的方差占比，和为1
pca.explained_variance_：投影后的特征维度的方差
pca.n_components_：保留的特征个数

使用样例

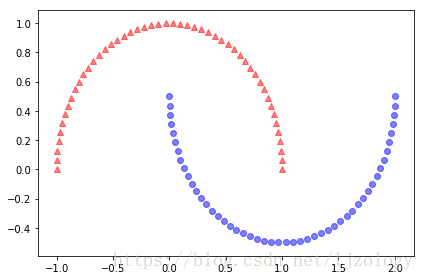
# 分离半月形数据，实现rbf_kernel_pca方法应用于非线性数据集
# 创建一个包含100个样本的二维数据集，以两个半月形状表示
import matplotlib.pyplot as plt
%matplotlib inline
# %matplotlib inline 可以在Ipython编译器里直接使用，功能是可以内嵌绘图，并且可以省略掉plt.show()这一步。
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=100, random_state=123)
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', marker='o', alpha=0.5)
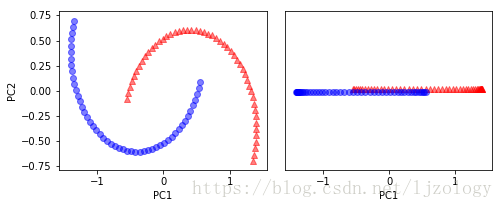
plt.tight_layout()

# 通过标准的PCA将数据映射到主成分上，对比原图
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(7,3))
ax[0].scatter(X_spca[y==0, 0], X_spca[y==0, 1], color='red', marker='^', alpha=0.5)
ax[0].scatter(X_spca[y==1, 0], X_spca[y==1, 1], color='blue', marker='o', alpha=0.5)

ax[1].scatter(X_spca[y==0, 0], np.zeros((50,1))+0.02, color='red', marker='^', alpha=0.5)
ax[1].scatter(X_spca[y==1, 0], np.zeros((50,1))-0.02, color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')

plt.tight_layout()
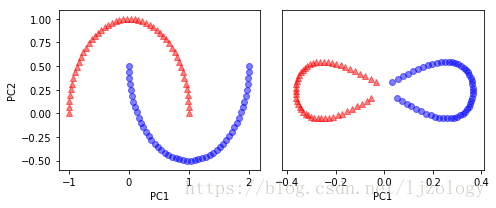
plt.show()

# kernel参数可选择不同的核函数
from sklearn.decomposition import KernelPCA

X, y = make_moons(n_samples=100, random_state=123)
scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
# 其中gamma的选值很重要，默认为1/n_features
X_skernpca = scikit_kpca.fit_transform(X)

fig, ax = plt.subplots(nrows=1,ncols=2, figsize=(7,3))

ax[0].scatter(X[y==0, 0], X[y==0, 1], color='red', marker='^', alpha=0.5)
ax[0].scatter(X[y==1, 0], X[y==1, 1], color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_skernpca[y==0, 0], X_skernpca[y==0, 1],color='red', marker='^', alpha=0.5)
ax[1].scatter(X_skernpca[y==1, 0], X_skernpca[y==1, 1],color='blue', marker='o', alpha=0.5)

ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')

plt.tight_layout()
plt.show()

参考文献

http://blog.codinglabs.org/articles/pca-tutorial.html
https://www.cnblogs.com/pinard/p/6243025.html
https://blog.csdn.net/ChenVast/article/details/79236160
周志华. 机器学习 : = Machine learning[M]. 清华大学出版社, 2016.