网络流——最大流EK算法讲解

网络流——最大流EK算法讲解

好了，这是第二篇博客了，如第一篇所述，来讲一讲刚刚理解的网络流。因为本人只会EK算法，所以先讲这个算法。（我会去补知识点的!!!）

一定翻到最后，中间不看都可以！！！

什么是网络流？？？

读者们刚接触这个知识可能会有点蒙，不，可能是非常蒙。虽然本蒟蒻也只是懵懵懂

如最短路，我想即使先不学，手算也能将一个简单的图求出来。

但是遇到网络流——最大流，那恐怕不是那么好算，反正一开始给我算我也只是一头雾水。（有可能是本人太弱了，各位大佬请谅解）

给个图（感谢某位大佬的图）

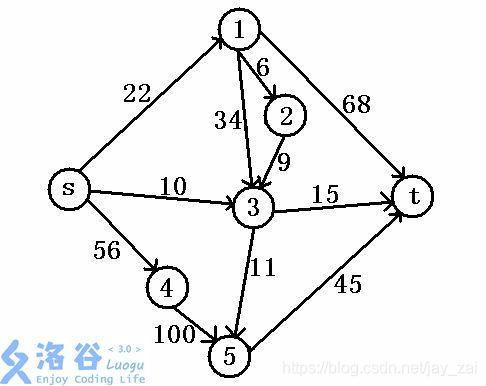
首先我们要先知道最大流的意思，简单来说有一个源点s，一个汇点t（如图），水流通过其他点从源点s到汇点t，请问可经过的最多水流。

那如上图，怎么求最大流呢？先手算一遍。

首先我们先理解理解：

图中的边权值意味着水流的最大流量（也许作者用词不精，但不妨碍理解吧？），即水流最大就边权值那么大。

我们再想想，水流怎么到达汇点的呢？显然，上述提及，是依靠其他点。那图中，有许多路径可从s到t，如：
s—>3—>t
s—>1—>t
s—>5—>t
s—>1—>3—>t
…
注意：图中所有的边都为有向边。

好了，那么先想：每一条路径的最大流量是多少呢？
。。。。。。
应为路径上的最小边权值。

why?

举个栗子：
两根钢管（别问哪来的）摆成“八”字（想像一下），随后一个小球从缝隙最大地方（“八”字底下）的往里滚，可想而知，若想让小球穿过钢管，那小球的最大直径应为钢管之间缝隙最小的距离。应该能懂吧？

so同理，最大流量应为最小边权值。抽象一下，因为水如果>最小边权，那流就炸了。

于是最大流为所有路径之和？

No！！！

以刚才那张图为例（再放一遍，因为我知道再翻上去有多麻烦！）

我们用s，1，2，3，t这几个点来举栗子

若按最大流为所有路径之和的思想，单看这几个点，ans应为：

s—>3—>t
流量：min（10,15）=10

s—>1—>t
流量：min（22,68）=22

s—>1—>3—>t
流量：min（22,34,15）=15

s—>1—>2—>3—>t
流量：min（22,6,9,15）=6

ans=10+22+15+6=53

对吗？错！！

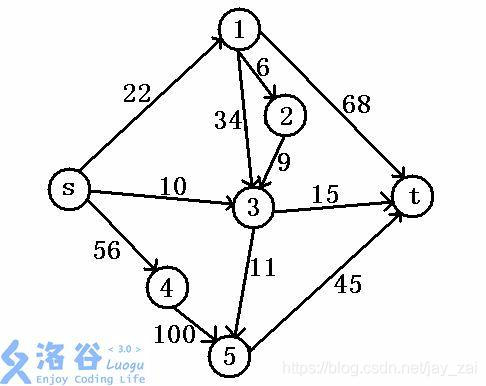
为什么错？
首先看到s，1；s，3 这两条边。可以看出边权为22,10。理解一下，（忽略点4,5）我就给了你这么多水，任你怎么去分配，仍不可能大于我原来给你的水。所以上述算的ans理论上就不是正确的。那么原因是什么？

以点1为例，s流入点1的水（22）会流向点3，点2，点t。那么思考，流向每一个点的水流都会是22吗？不会。22是分配给了这三个点，所以应该是22为流向3个点的总和。

但注意，路径途中看可能会有水流失，如s—>4的水流就流失了，5—>t流不到56。

那正解呢?单说这道题，通过我们人的智慧，脑中应可以想出个贪心（应该是吧？）如点1，点2汇到点3想一想完全不需要。虽然3—>t还会多出5的流量，可以选择再补一点，但是补的是哪里的呢？s—>1的22里面的。那我完全可以将这22全从1汇入t，一次性搞定那不香吗 。所以用不着将点1的水汇一些给点3。

再举个栗子：3—>5其实也不需要走，因为：

1. s汇给3的流量10完全可以直接从3—>t汇入，而且可以汇完，与上所说一样，所以不用汇给5。
2. s—>4就给了56的流量，这的流量从5—>t都汇不完，但我再加个（11）3—>5又有什么用呢？

所以大概的思路就有了，那么依靠我们自身的判断，上图最大流应为22+10+45=77。

好了，我们总算手玩一遍了，那这种思想可以与程序结合吗？答案是肯定的。但是做到这一点还有一个问题：

上面说的什么什么路径不用走，是靠我们人的判断想出来的，但机器是死的，如何让它知道该走哪一条路呢？如果不注意这个问题，那结果即是得不到最优解。

当然，读者们也许还不知道如何先求最大流（也就是抛开上面问题的程序实现），但别着急，我们理解了这么多吗，还是先理解一些定义。（下面只是介绍，助于理解，看不懂没关系，但是有些必需看懂的等会会提醒。）

网络流、最大流定义

这就是硬东西了：
一、网络流的定义：有向图G=(V,E)中，点集中有一源点S，一汇点T。且S入度为0，T出度为0。对于每条边edge，都有一权值函数c，表示其容量，一权值函数f，表示其实际流量。

二、最大流的定义：在不违背网络流的定义下，S到T的最大流量。

好了，不管看不看的懂，没事，知道什么是网络流，什么是最大流就行了。（其实是自己也不太清楚，也说不清楚 ）

那么刚刚我们就有了一个初步的思路，找到一条路径，ans+=min（边权）。对了，因为是手算，没说一个要点，（别怪我）

要点：想一想，但我们找到一条路径时，得到一个答案时，是不是路径上每一条边权都要减去最小边权呢。对吧？换到生活上，也是如此。因为一个边权，通过此边权有一条路径，那我分配了一些水过去，那自身流量是不是也要减少？因为我剩下的流量要给其他未被找到的路径用，不可能把分配过的水再次用，那这样就错了。

这是实现程序的一个步骤。

还有一个定义：

增广路：

增广路是指从s到t的一条路，流过这条路，使得当前的流（可以到达t的人）可以增加。

这个东西其实就是刚刚说的路径，但更加详细。

那么求最大流问题可以转换为不断求解增广路的问题，并且，显然当图中不存在增广路时就达到了最大流。

思路如下：

1. 找到一条路径（即增广路），这里用bfs实现。
2. 再得到路径的最小边权，累加答案，并且路径中的边权减去其。（这样也避免宽搜里死循环）
3. 路径反向边加上最小边权。
4. 重复此过程，直到结束循环，此情况下也便找到了最大流。

那么程序就这么easy！！！

什么鬼？所以上述3是什么（what？），为什么（why？），怎么用（how？）

好吧，其实这个步骤也就是来解决刚刚我们说过的问题:

梳理一下即是：在做增广路时可能会阻塞后面的增广路，或者说，做增广路本来是有个顺序才能找完最大流的。

为什么加反向边？

其实也就是给予程序一个反悔的机会。

因为我们是任意找的，为了修正，就每次将流量加在了反向弧上（其实就是反向边），让后面的流能够进行自我调整。

其实就是把一个路径的一条边退了回去，让它走另一条路径。

若你还是有些懵，没事，先看看代码。

所以说，这就是最大流的解法（其一），你如果理解了反向边的概念。那恭喜你，成功理解了

EdmondsKarp算法

这里先说一下复杂度为：
O(VE^2)

EK算法还是很容易理解的，并且代码实现很简单，当整个图是稀疏图的时候，使用EK算法不失为一种简便可行的方法，但是如果图的边数非常多，这个算法的性能也就显得不是那么优秀。可以看到EK算法的处理在每次找到增广路后，就从源点开始重新再BFS遍历查找，这一过程中有很多的遍历都是没必要的，虽然其他算法我也不会。

跟着思路放一下代码：

找到一条路径（即增广路），这里用bfs实现。

int bfs(){
	memset(b,1,sizeof(b));
	int np,flow=inf;//np为队首，flow为最小边权
	queue<int>q;//队列
	q.push(1);//1开始bfs
	b[1]=0;//标记
	pre[1]=pre[n]=-1;//pre[i]表示i点的上一个点，也就是从pre[i]走向i
	while(!q.empty()){
		np=q.front();//取出队首
		q.pop();//出队
		if(np==n)break;//搜到n，即找到一条路径，break
		for(int i=1;i<=n;i++)
			if(b[i]&&g[np][i]!=0){//没被搜过，且有边
				b[i]=0;//标记
				pre[i]=np;//记录前一个点
				q.push(i);//入队
				flow=min(flow,g[np][i]);//flow取最小值
			}
	}
	if(pre[n]==-1)return 0;//pre[n]=1说明没搜到最短路径
	else return flow;//搜到就返回最小边权
}

再得到路径的最小边权，累加答案，并且路径中的边权减去其。（这样也避免宽搜里死循环）路径反向边加上最小边权。

int EK(){
	int stream,u,sum=0;//stream为返回的最小边权值，u为路径点，sum为最大流答案
	while((stream=bfs())!=0){//当边权值！=0说明还有路径
		sum+=stream;//累计答案
		u=n;//n为最后一个点，u从最后一个点开始往回推
		while(pre[u]!=-1){//u的前一个=-1说明u=1了，那就退出循环
			g[pre[u]][u]-=stream;//从pre[u]到u的边权减去最小权值
			g[u][pre[u]]+=stream;//u到pre[u]即为反向边，加上权值
			u=pre[u];//u=上一个点，推回去
		}
	}
	return sum;//最大流答案
}

OK
这里先放一个题目，再放完整代码，读者也可以先去理解程序。

Drainage Ditches草地排水

题目描述：在农夫约翰的农场上，每逢下雨，贝茜最喜欢的三叶草地就积聚了一潭水。这意味着草地被水淹没了，并且小草要继续生长还要花相当长一段时间。因此，农夫约翰修建了一套排水系统来使贝茜的草地免除被大水淹没的烦恼（不用担心，雨水会流向附近的一条小溪）。作为一名一流的技师，农夫约翰已经在每条排水沟的一端安上了控制器，这样他可以控制流入排水沟的水流量。
农夫约翰知道每一条排水沟每分钟可以流过的水量，和排水系统的准确布局（起点为水潭而终点为小溪的一张网）。需要注意的是，有些时候从一处到另一处不只有一条排水沟。
根据这些信息，计算从水潭排水到小溪的最大流量。对于给出的每条排水沟，雨水只能沿着一个方向流动，注意可能会出现雨水环形流动的情形。

INPUT FORMAT 输入格式

第1行: 两个用空格分开的整数N (0 <= N <= 200) 和 M (2 <= M <= 200)。N是农夫约翰已经挖好的排水沟的数量，M是排水沟交叉点的数量。交点1是水潭，交点M是小溪。

第二行到第N+1行: 每行有三个整数，Si, Ei, 和 Ci。Si 和 Ei (1 <= Si, Ei <= M) 指明排水沟两端的交点，雨水从Si 流向Ei。Ci (0 <= Ci <= 10,000,000)是这条排水沟的最大容量。

OUTPUT FORMAT 输出格式

输出一个整数，即排水的最大流量。

样例

5 4

1 2 40

1 4 20

2 4 20

2 3 30

3 4 10

输出

50

题目解析

这道题就是一个裸最大流，直接套用即可。n,m<=200，EK算法。当然，会dinic之类更快算法的大佬们可以尝试数据加强版。

代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<queue>
#define inf 0x3f3f3f3f//无穷大
using namespace std;
int n,m,u,v,e;
int g[207][207],pre[207];
bool b[207];
int bfs(){
	memset(b,1,sizeof(b));
	int np,flow=inf;//np为队首，flow为最小边权
	queue<int>q;//队列
	q.push(1);//1开始bfs
	b[1]=0;//标记
	pre[1]=pre[n]=-1;//pre[i]表示i点的上一个点，也就是从pre[i]走向i
	while(!q.empty()){
		np=q.front();//取出队首
		q.pop();//出队
		if(np==n)break;//搜到n，即找到一条路径，break
		for(int i=1;i<=n;i++)
			if(b[i]&&g[np][i]!=0){//没被搜过，且有边
				b[i]=0;//标记
				pre[i]=np;//记录前一个点
				q.push(i);//入队
				flow=min(flow,g[np][i]);//flow取最小值
			}
	}
	if(pre[n]==-1)return 0;//pre[n]=1说明没搜到最短路径
	else return flow;//搜到就返回最小边权
}
int EK(){
	int stream,u,sum=0;//stream为返回的最小边权值，u为路径点，sum为最大流答案
	while((stream=bfs())!=0){//当边权值！=0说明还有路径
		sum+=stream;//累计答案
		u=n;//n为最后一个点，u从最后一个点开始往回推
		while(pre[u]!=-1){//u的前一个=-1说明u=1了，那就退出循环
			g[pre[u]][u]-=stream;//从pre[u]到u的边权减去最小权值
			g[u][pre[u]]+=stream;//u到pre[u]即为反向边，加上权值
			u=pre[u];//u=上一个点，推回去
		}
	}
	return sum;//最大流答案
}
int main(){
	scanf("%d%d",&m,&n);
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&u,&v,&e);
		g[u][v]+=e;//邻接矩阵存表
	}
	printf("%d",EK());
} 

对于刚学网络流最大流的读者，下面再给一道例题（稍微变形一点，需自行连边构图，若上面的知识懂了可以看一看，若上面的还未消化完毕，则可以放一放）

Description 描述

Merlin想从n个不同的网站分别下载一个文件，每个网站有各自限定的带宽。也就是说，Merlin在一个网站下载该文件时，每秒钟只能下载不超过带宽大小的字节数。此外，每个网站还有各自的服务时间，Merlin只可以在给定的时间段内下载文件，否则网站会拒绝Merlin的请求。最后，Merlin的电脑也有带宽限制，每秒钟下载的总字节数不能超过给定的带宽。
　　由于Merlin的电脑足够强大，将一个文件下载的各个部分重新合并成整个文件的时间可以忽略。每次下载文件时必须下载整数字节。
　　现在请问：Merlin是否能在给定的时间内下载完所有的文件？

输入

对于每组数据，第一行是三个整数n，w和s，n是要下载的文件数，w（位/秒）是Merlin电脑的总容量，表示每秒最多能下载的字节数，而s则是Merlin下载这些文件的时间限制，表示Merlin可以下载的时间为第1秒到第s秒（包含第1秒和第s秒）。
　　
接下来有n行，每行表示一个文件的信息。每行有四个整数ai，bi，ci和di（1 <= ai，bi <= 100,000，1 <= ci <= di <= s）。它们表示这个文件可以从第大小为ai（位）而这个文件所在的网站的宽度是bi（位/秒）。

n = 0时表示输入文件结束。ci 秒（含ci）开始下载，直到第di秒（含di）。

输出

对每组数据，如果Merlin能在s秒内下载完所有n个文件，输出一行 “yes”，否则输出一行 “no”。

样例输入

3 100 4
100 50 1 2
100 50 2 3
100 100 4 4
3 100 4
100 50 1 2
100 50 2 3
100 100 3 3
0

样例输出

yes
no

题目解析

看了第一眼，这什么鬼呀，怎么do？

上述说了，需自行构边。

**如何构边呢？**样例第一组数据为例，图来！！！

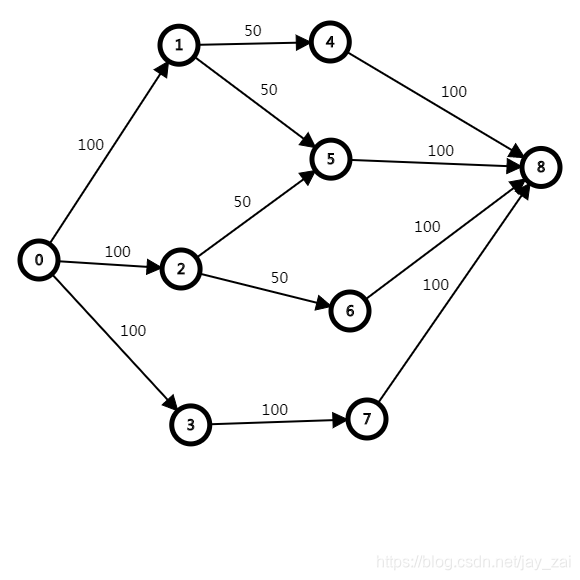
本来是自己一个小菜鸡画的水图，结果某位无名巨佬给了张图,膜拜，膜拜！！！

好了，你肯定看不懂，但我知道。首先节点0是一个“超级节点”，也是源点。连向1,2,3是三个文件，之间的权值是文件大小。

其次，4,5,6,7是时间，i节点存i-n（文件数量）秒，点1,2,3指向自己可下载的秒数，权值为每秒下载带宽。然后时间指向另一个“超级节点”，也是汇点（图中是8，为n+s+1），权值为Merlin电脑的带宽。

随后跑一遍最大流就OK了，至于为什么这样构图可以思考思考。

最大流程序就不给了，给一下建图的程序：（有点丑）

int main(){
	scanf("%d",&n);//多数据
	while(n!=0){//=0就结束
		m=0;//m记录需要下载的总大小，与最大流比较，m<ans就可以
		scanf("%d%d",&w,&s);//
		for(int i=1;i<=n;i++){
			scanf("%d%d%d%d",&a[i],&b[i],&c[i],&d[i]);
			m+=a[i];//m加上文件大小
			g[0][i]=a[i];//0到文件建边
			for(int j=c[i];j<=d[i];j++) g[i][n+j]=b[i];//文件到时间建边
		}
		for(int i=1;i<=s;i++)g[n+i][n+s+1]=w;//时间到汇点建边
		if(EK(0,n+s+1)>=m)printf("yes\n");//判断
		else printf("no\n");
		memset(pre,0,sizeof(pre));//初始化
		memset(g,0,sizeof(g));
		scanf("%d",&n);//再次读入
	}
}

这是第二篇博客，也是第一篇讲算法，若有疏忽，请谅解。也请多多支持，若觉得写的可以就请您高抬贵手，给个赞吧，以资鼓励。谢谢各位大佬！！！