0
动态规划的思路:当分析前i个对象的取舍时,在约束条件所有可能取值的情况下,先分别求出每一个约束条件取值下子问题的最优解,这样在分析第i+1个对象加入的情况下,就可以直接调用之前已经分析的其中一个或者多个子问题的解,这些子问题的其他解可能不是局部最优的解,但是考虑到第i+1个对象,他们可能就是最后的最优解的组成部分之一。
动态规划大部分也是运用穷举思想,但是:
- 第一是只会穷举每个子问题的最优解。
- 第二是通过状态刷新求新的最优解,因为之前子问题的解已经被存储,新的子问题到来时只需要做出O(n)次max比较并且存储新解即可。
动态规划解题步骤
问题抽象化、建立模型、寻找约束条件、判断是否满足最优性原理、找大问题与小问题的递推关系式、填表、寻找解组成。
背包问题
在解决问题之前,为描述方便,首先定义一些变量:Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积,定义V(i,j):当前背包容量 j,前 i 个物品最佳组合对应的价值,同时背包问题抽象化(X1,X2,…,Xn,其中 Xi 取0或1,表示第 i 个物品选或不选)。
-
建立模型,即求max(V1X1+V2X2+…+VnXn);
-
寻找约束条件,W1X1+W2X2+…+WnXn<capacity;
-
寻找递推关系式,面对当前商品有两种可能性:
- 包的容量比该商品体积小,装不下,此时的价值与前i-1个的价值是一样的,即V(i,j)=V(i-1,j);
- 还有足够的容量可以装该商品,但装了也不一定达到当前最优价值,所以在装与不装之间选择最优的一个,即V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)}。
其中V(i-1,j)表示不装,V(i-1,j-w(i))+v(i) 表示装了第i个商品,背包容量减少w(i),但价值增加了v(i);
由此可以得出递推关系式:
- j<w(i) V(i,j)=V(i-1,j)
- j>=w(i) V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)}
背包问题最优解回溯:
通过上面的方法可以求出背包问题的最优解,但还不知道这个最优解由哪些商品组成,故要根据最优解回溯找出解的组成,根据填表的原理可以有如下的寻解方式:
V(i,j)=V(i-1,j)时,说明没有选择第i 个商品,则回到V(i-1,j);
V(i,j)=V(i-1,j-w(i))+v(i)时,说明装了第i个商品,该商品是最优解组成的一部分,随后我们得回到装该商品之前,即回到V(i-1,j-w(i));
一直遍历到i=0结束为止,所有解的组成都会找到。
例题:
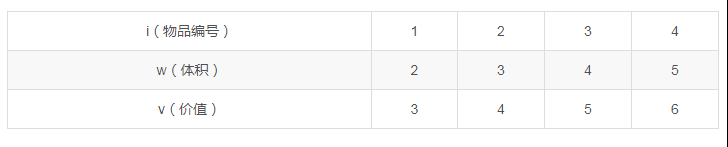

最优解为V(4,8)=10,而V(4,8)!=V(3,8)却有V(4,8)=V(3,8-w(4))+v(4)=V(3,3)+6=4+6=10,所以第4件商品被选中,并且回到V(3,8-w(4))=V(3,3);
有V(3,3)=V(2,3)=4,所以第3件商品没被选择,回到V(2,3);
而V(2,3)!=V(1,3)却有V(2,3)=V(1,3-w(2))+v(2)=V(1,0)+4=0+4=4,所以第2件商品被选中,并且回到V(1,3-w(2))=V(1,0);
有V(1,0)=V(0,0)=0,所以第1件商品没被选择。
详细代码实现如下:
#include<iostream>
using namespace std;
#include <algorithm>
int w[5] = {
0 , 2 , 3 , 4 , 5 }; //商品的体积2、3、4、5
int v[5] = {
0 , 3 , 4 , 5 , 6 }; //商品的价值3、4、5、6
int bagV = 8; //背包大小
int dp[5][9] = {
{
0 } }; //动态规划表
int item[5]; //最优解情况
void findMax() {
//动态规划
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= bagV; j++) {
if (j < w[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
}
void findWhat(int i, int j) {
//最优解情况
if (i >= 0) {
if (dp[i][j] == dp[i - 1][j]) {
item[i] = 0;
findWhat(i - 1, j);
}
else if (j - w[i] >= 0 && dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
item[i] = 1;
findWhat(i - 1, j - w[i]);
}
}
}
void print() {
for (int i = 0; i < 5; i++) {
//动态规划表输出
for (int j = 0; j < 9; j++) {
cout << dp[i][j] << ' ';
}
cout << endl;
}
cout << endl;
for (int i = 0; i < 5; i++) //最优解输出
cout << item[i] << ' ';
cout << endl;
}
int main()
{
findMax();
findWhat(4, 8);
print();
return 0;
}
最长递增子序列问题
思路:
- 定义dp的含义,比如这一题,dp是一个数组,dp[i]表示的是,在确定必须选择v[i]的情况下,表示v[0…i]中的最长递增子序列的长度。
- 写出递归式或者状态转换方程:dp[i] = max(dp[j]) + 1 当v[i]>v[j]时
- 定义最优值,这里的最优值可能是dp中的某一项。如LISLength = max(dp[i])
例题:
计算最少出列多少位同学,使得剩下的同学排成合唱队形
说明:
N位同学站成一排,音乐老师要请其中的(N-K)位同学出列,使得剩下的K位同学排成合唱队形。
合唱队形是指这样的一种队形:设K位同学从左到右依次编号为1,2…,K,他们的身高分别为T1,T2,…,TK, 则他们的身高满足存在i(1<=i<=K)使得T1<T2<…<Ti-1Ti+1>…>TK。
你的任务是,已知所有N位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
注意:不允许改变队列元素的先后顺序 且 不要求最高同学左右人数必须相等
请注意处理多组输入输出!
备注:
1<=N<=3000
输入描述:
有多组用例,每组都包含两行数据,第一行是同学的总数N,第二行是N位同学的身高,以空格隔开
输出描述:
最少需要几位同学出列
示例1
输入:
8
186 186 150 200 160 130 197 200
复制
输出:
4
求解:
这题抛开场景,核心问题是最长递增子序列,可以参考leetcode 最长递增子序列 来理解。
总的来说,就是自左向右求出最长递增子序列的最优值dp数组,自右向左求出最长递减子序列的最优值dp数组,两者对位相加-1,其中的最大值,就是整个合唱队留在场上的人数的最大值,因此也就是出列的最小值。
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int n;
while(cin >> n){
// 输入的数组
int tmp;
vector<int> v;
for (int i = 0; i < n; ++i){
cin >>tmp;
v.push_back(tmp);
}
// 最长递增子序列
if (v.empty()) return 0;
vector<int> dp1(n, 0);
for (int i = 0; i < n; ++i){
dp1[i] = 1;
for(int j = 0; j < i ; ++j){
if (v[i] > v[j]){
dp1[i] = max(dp1[i], dp1[j]+1);
}
}
}
// 最长递减子序列
vector<int> dp2(n, 0);
for (int i = n - 1; i >= 0; --i){
dp2[i] = 1;
for (int j = n -1; j > i; --j){
if (v[i] > v[j]){
dp2[i] = max(dp2[i], dp2[j]+1);
}
}
}
int maxLength = 0;
for (int i = 0; i < n; ++i){
if (maxLength < dp1[i] + dp2[i] - 1){
maxLength = dp1[i] + dp2[i] - 1;
//这里的i就是划分中点
}
}
cout << n - maxLength << endl;
}
return 0;
}