多项式全家桶 基础知识+各种操作+例题（细节证明）

前置知识

因为大多数这些题要取模一个质数，不取模的话NTT也可以想办法替代常数上天误差极大的FFT，因此我们只需要了解快速数论变换NTT。

这里贴一份笔者的模板：

int xm[MAXN<<2],om,rev[MAXN<<2];// 工具数组
int qkpow(int a,int b,int MD) {
    
     // 必要模板：快速幂
	int res = 1; while(b > 0) {
    
    
		if(b & 1) res = res *1ll* a % MD;
		a = a *1ll* a % MD; b >>= 1;
	}return res;
}
const int RM = 3;     // 原根（随MOD而定，不一定是3）
// 正片开始
void NTT(int *s,int n) {
    
    
	for(int i = 1;i < n;i ++) {
    
    
		rev[i] = ((rev[i>>1] >> 1) | ((i&1) ? (n>>1):0));
		if(rev[i] < i) swap(s[rev[i]],s[i]);
	}
	om = qkpow(RM,(MOD-1)/n,MOD); xm[0] = 1;
	for(int k = 1;k < n;k ++) xm[k] = xm[k-1]*1ll*om % MOD;
	for(int k = 2,t = (n>>1);k <= n;k <<= 1,t >>= 1)
		for(int j = 0;j < n;j += k)
			for(int i = j,l = 0;i < j+(k>>1);i ++,l += t) {
    
    
				int A = s[i],B = s[i+(k>>1)];
				s[i] = (A + xm[l]*1ll*B%MOD) % MOD, s[i+(k>>1)] = (A +MOD- xm[l]*1ll*B%MOD) % MOD;
			}
	return ;
}
void INTT(int *s,int n) {
    
     // 完全可以写到一个函数里
	for(int i = 1;i < n;i ++) {
    
    
		rev[i] = ((rev[i>>1] >> 1) | ((i&1) ? (n>>1):0));
		if(rev[i] < i) swap(s[rev[i]],s[i]);
	}
	om = qkpow(qkpow(RM,(MOD-1)/n,MOD),MOD-2,MOD); xm[0] = 1;
	for(int k = 1;k < n;k ++) xm[k] = xm[k-1]*1ll*om % MOD;
	for(int k = 2,t = (n>>1);k <= n;k <<= 1,t >>= 1)
		for(int j = 0;j < n;j += k)
			for(int i = j,l = 0;i < j+(k>>1);i ++,l += t) {
    
    
				int A = s[i],B = s[i+(k>>1)];
				s[i] = (A + xm[l]*1ll*B%MOD) % MOD, s[i+(k>>1)] = (A +MOD- xm[l]*1ll*B%MOD) % MOD;
			}
	int invn = qkpow(n,MOD-2,MOD);
	for(int i = 0;i <= n;i ++) s[i] = s[i] *1ll* invn % MOD;
	return ;
}

如果一道题非要用 $FFT$ 的话，那么结果肯定不会超过 $longlong$，我们只需要一个超过 $FFT$ 结果范围的可以做 $NTT$ 的质数，以及 $O(1)$ 光速乘。

笔者用 $MillerRabbin$ 算法算出了三个合适的质数：

• 1000000000245104641 ($2^{25}\ast 29802322395+1$)
  ($>1e18$)
  原根：7
• 4000000000149946369 ($2^{23}\ast 476837158221+1$)
  ($>4e18$)
  原根：13
• 9000000000461111297 ($2^{25}\ast 268220901503+1$)
  ($>9e18$)
  原根：3

基础知识

求导

这个并不局限于多项式函数，应该任意函数都行，但是求导后我们会失去原函数在 $y$ 轴上的具体位置，再求不定积分就会失去多项式或者其他函数泰勒展开后的 0 次项。

定义就不必多说了吧，可以自行百度。

主要是一些知识要记背，我们令 $f^{\prime }$ 表示 $f$ 的导函数，用 $f^{(k)}$ 表示 $f$ 的 $k$ 阶导（求 $k$ 次导）

• $(f+g{)}^{\prime }=f^{\prime }+g^{\prime }$
• $f(x)=-g(x),f^{\prime }(x)=-g^{\prime }(x)$
• 链式法则：$(f(g(x)){)}^{\prime }=f^{\prime }(g(x))\cdot g^{\prime }(x)$

常用导函数：

• $f(x)=x^a,f^{\prime }(x)=a\cdot x^{a-1}$
• $f(x)=a^x,f^{\prime }(x)=a^x\cdot \ln a\Rightarrow f(x)=e^x,f^{\prime }(x)=e^x=f(x)$
• $f(x)=\ln x,f^{\prime }(x)=\frac{1}{x}=x^{-1}$
• $f(x)=\sin x,f^{\prime }(x)=\cos x$
• $f(x)=\cos x,f^{\prime }(x)=-\sin x\Rightarrow f(x)=\sin x,f^{(4)}(x)=\sin x$

知道这些是为了方便地计算以多项式为自变量的函数的导函数，因为不一定是多项式函数，所以导函数需要另外记背。

泰勒展开

对于任意函数 $f(x)$ ，都可以通过导函数表示成多项式函数的形式

具体先选一个位置 $x_0$ 为出发点（不一定非要是 0，但一般定义域允许的话就设成 0），然后
$$f(x)=f(x_0)+\frac{f^{\prime }(x_0)}{1!}(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\cdots \cdots$$$$=\sum _{i=0}^{\infty }\frac{f^{(i)}(x_0)}{i!}(x-x_0{)}^i$$

如果是多项式函数，那么上式中的项一定是有限的，但其它函数就不一定了。

特别地，$x_0=0$ 时的公式叫麦克劳林公式。

另外，因为 $e^x$ 导函数是其本身，所以令 $x_0=0$，我们可以得出

$$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots \cdots$$

这是 $e^x$（$exp(x)$）的定义式，同时也是指数型母函数的基本结论，这就牵扯到生成函数了，和多项式关系极其密切，但是这里先不展开。

操作讲解

无泰勒展开

先讲讲轻松的吧，不需要用到泰勒展开或是后面要提到的牛顿迭代

多项式求导 & 积分

根据 $(f+g{)}^{\prime }=f^{\prime }+g^{\prime }$ 以及 $(x^a{)}^{\prime }=a\cdot x^{a-1}$ 我们可以 $O(n)$ 的进行多项式求导，把每一项分别求导就行，积分则只需要倒着算。

多项式逆元

已知多项式函数 $f$ ，求 $g$ ，满足

$$f\ast g\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

先讲讲这个取模的意义，相当于是把函数第 $n$ 次项以及后面的全部删去，不然的话也谈不上算逆元了
这里的 1 实际上表示一个前 $1$ 到 $n-1$ 次项都为 0，0 次项为 1 的多项式函数
这里的 $x$ 并不是一个常数，不能用常数的一些法则去看待它，但是一些性质是有的，比如$$f\mathrm{m}\mathrm{o}\mathrm{d}{x}^k=0\Rightarrow f\mathrm{m}\mathrm{o}\mathrm{d}{x}^{k-1}=0$$所以我们不妨把 $n$ 定为一个更大的 2 的幂

假设我们已经知道了函数 $h$ 满足 $f\ast h\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{\frac{n}{2}})$，现在要求 $g$，
现在先变个式：

$$f\ast h-1\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{\frac{n}{2}})$$

由于后面的 0 表示前 n/2 项为 0 的函数，至少到 n/2 次项才可能有值，平方后最低次的有值的项也至少是 n 次项，因此取模 $x^n$ 后还是 0 ，我们把式子两侧平方：

$$(f\ast h-1{)}^2\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

展开：

$$f^2\ast h^2-2f\ast h+1\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

由于我们知道 $f\ast g\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$，把同余式两边同乘 $g$：

$$f\ast h^2-2h+g\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

移项，得到倍增公式：

$$g\equiv 2h-f\ast h^2\equiv h(2-f\ast h)(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

于是，我们可以用同样的方法先求出 $h$，取模 $x^1$ 时直接常数求逆元，这样算法时间 $T(n)=T(\frac{n}{2})+n\log n$，总时间复杂度 $O(n\log n)$。

多项式取模多项式 & 多项式除法

求多项式 $q,r$ 满足

$$f=q\ast g+r$$

其中 $f,g$ 都是多项式，没有取模 $x^n$，$r$ 的次数要小于 $g$。

这个做起来很麻烦，而且没有取模，又不常用，笔者就贴个链接吧：万能的Wiki

简单说一下，就是一个结论，设 $f$ 是 $n$ 次的，$g$ 是 $m$ 次的，$f_r$ 表示 $f$ 的系数翻转，

$$f_r\equiv q_r{g}_r(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

$$q_r\equiv f_r{g}_r^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

然后多项式减法求出 $r$ 就行了。

多项式最大公因式 & 最小共倍式

好吧其实多项式取模和除法还是挺有用的，比如可以用来求多项式最大公因式(次数最大)和最小公倍式(次数最小)。

求最大公因式要用到辗转相除法，即对于两个多项式 $f,g$，最大公因式为

$$(f,g)=(g,f\%g)$$

其中的取模就是多项式取模多项式。

求最小共倍式跟正整数类似，多项式 $f,g$ 的最小共倍式为

$$[f,g]=\frac{f\ast g}{(f,g)}$$

其中的除法是多项式除法，不过，这里保证了能整除，因此我们可以用多项式求逆+乘法。

一些性质：

①设 $f$、$g$ 是数域 $P$ 上的多项式且不全为 0，则其最大公因式一定存在。
②若 $d$ 与 $d_1$ 都是 $f$ 和 $g$ 的最大公因式，那么 $d$ 与 $d_1$ 最多相差一个非零常数因子，即 $d=c{d}_1$（c 是常数）。
③若 $d$ 与 $d_1$ 都是 $f$ 和 $g$ 的最小共倍式，那么 $d$ 与 $d_1$ 最多相差一个非零常数因子，即 $d=c{d}_1$（c 是常数）。
因此最大公因式和最小共倍式并不唯一。

这个并不是没用的知识点，事实上它在题目中出现了。详见文末例题。

多项式自然对数

即求一个多项式 $g$

$$g\equiv \ln f(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

$f$ 是个多项式。

$\ln$ 确实不好求，但是我们知道它的导函数是 $\frac{1}{x}$ ，所以我们可以先牺牲掉 $f$ 的 0 次项，把它求导再求不定积分：

$$g\equiv \int ((\ln f{)}^{\prime })\equiv \int (\frac{1}{f}\cdot f^{\prime })$$

我们用一个多项式求逆就行了。

然后它的 0 次项怎么办？我们代值试试，它的 0 次项必然是 $\ln f(0)$，由于除了 $\ln 1=0$ 以外，其他整数的 $\ln$ 值都不好求，所以一般题目中出现多项式自然对数就一定保证了 $f$ 的 0 次项（f(0)）为 1，同时 $\ln f(0)=0$，结果的 0 次项为 0，不然无法求自然对数。

泰勒展开应用：牛顿迭代

牛顿迭代就是求一个多项式 $g$ ，满足

$$f(g)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

$f$ 不一定为多项式。

首先，我们还是令 n 为更大的 2 的幂，然后假设我们已经求出来了 $f(h)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{\frac{n}{2}})$，我们把它当做泰勒展开中的“$x_0$”，代入泰勒展开试试：

$$0\equiv f(g)\equiv f(h)+f^{\prime }(h)(g-h)+\frac{f^{\prime \prime }(h)}{2!}(g-h{)}^2+...(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$
由于我们求出的 $h\equiv g(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{\frac{n}{2}})$，可得

$g-h\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{\frac{n}{2}})\Rightarrow (g-h{)}^2\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n),(g-h{)}^3\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)...$

所以上面的展开式中只有前两项留了下来，其它项都变成了 0，式子就变成了：

$$0\equiv f(h)+f^{\prime }(h)(g-h)(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

$$g\equiv h-\frac{f(h)}{f^{\prime }(h)}(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

这便是牛顿迭代公式了，根据这一公式先算出 $h$ 。

至于边界，取模 $x^1$ 的情况，就可以直接把要求的函数看成一个未知数去求函数零点就行了。

多项式exp

求 $g$

$$g\equiv e^f(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

其中 $f$ 是个多项式。

由于 exp 函数的导函数等于它本身，所以我们不能用解多项式ln的思路解它。

那么我们先两边求自然对数：

$$\ln g\equiv f(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

$$\ln g-f\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

然后我们令 $F(g)=\ln g-f$（同时 $F^{\prime }(g)$ 就等于 $\frac{1}{g}$，$f$ 此时算常数项），那么就等同于

$$F(g)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

使用牛顿迭代！假设已经求出 $F(h)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{\frac{n}{2}})$

$$g\equiv h-\frac{F(h)}{F^{\prime }(h)}(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

$$g\equiv h-\frac{\ln h-f}{\frac{1}{h}}\equiv h(1-\ln h+f)(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

那么最后一步就是算边界了，那自然是一个数而不是多项式，且等于 $e^{f(0)}$，由于只有 $e^0=1$ 好算，所以题目中一般出现exp，f 的 0 次项就为 0，同时 $e^{f(0)}=1$，不然无法计算。

算法时间 $T(n)=T(\frac{n}{2})+n\log n$，时间复杂度 $O(n\log n)$.

多项式任意幂

既然我们学了多项式乘法，又学了快速幂，于是我们就会了多项式快速幂，复杂度 $O(n{\log }^{2}n)$，这很棒。
但是如果这个幂特别大，超过int，超过long long，甚至你得别读入边取模才行？或者是一个分数，负数，有理数（模意义下是整数）？又或者，你只是想让理论复杂度少个 $\log$？那必须了解一下多项式任意幂！
By the way，多项式幂可不适用费马小定理。

求多项式 $g$

$$g\equiv f^k(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$其中 $f$ 是个多项式。

鱼和熊掌不可兼得，我们既然要让 $k$ 可以为任意有理数，那么必须要有点牺牲才行，

$$\ln g\equiv \ln (f^k)(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

那就是，$f$ 的 0 次项必须是 1，因为我们要取 $\ln$ ，为什么是 1 笔者之前分析过，这里不展开。继续变式：

$$\ln g\equiv k\ln f(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

$$e^{\ln g}\equiv e^{k\ln f}(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

$$g\equiv e^{k\ln f}(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

使用我们之前学的多项式自然对数和多项式exp，时间复杂度 $O(n\log n)$。

是不是很神奇！虽然它常数特别大，但是把不好优化的 $\log$ 变成了容易优化的常数，给了常数大神们一个发挥的空间。

最后，我们看到有的题中 $f$ 的 0 次项不为 1，那么我们把它化成 1 就是了

$$f^k={\left(\frac{f}{f(0)}\right)}^k\ast f(0{)}^k$$

多项式开根

求 $g$ 满足

$$g^2\equiv f(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

其中 $f$ 是个多项式。

不说了，$g\equiv f^{\frac{1}{2}}(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$，直接多项式幂。

还是推一推吧，

$$g^2-f\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

令 $F(g)=g^2-f,F^{\prime }(g)=2g$，那么

$$F(g)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

使用牛顿迭代！假设已经求出 $F(h)\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}{x}^{\frac{n}{2}})$

$$g\equiv h-\frac{F(h)}{F^{\prime }(h)}(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

$$g\equiv h-\frac{h^2-f}{2h}\equiv \frac{1}{2}(h+\frac{f}{h})(\mathrm{m}\mathrm{o}\mathrm{d}{x}^n)$$

看吧，其实常数也没小多少（我的天哪常数居然小了一半！），复杂度还是 $O(n\log n)$，所以，要是不想记开根公式，可以直接用多项式幂，但是作为追求更快的我们来说，这个还是有必要记的。

另外，在loj挑战多项式中，多项式开根的常数项不是 1 ，但是保证了是模数的二次剩余，所以我们要把边界处的常数项求一个二次剩余，具体是用模数的原根跑大步小步算法，由于是原根所以大步小步跑出的是唯一解，因为保证是二次剩余，所以大步小步的结果一定是个偶数，可以除以二再算原根的幂……可以看看yyb的博客，笔者就不展开了。

模板

没有多项式除法，但是多项式除法用其它板子直接计算就行了，其实没必要贴。

const int MOD = 998244353;
int xm[MAXN<<2],om,rev[MAXN<<2];// tool
int qkpow(int a,int b) {
    
     // It's necessary
	int res = 1; while(b > 0) {
    
    
		if(b & 1) res = res *1ll* a % MOD;
		a = a *1ll* a % MOD; b >>= 1;
	}return res;
}
const int RM = 3;     // Prime Root
// Let's Start
void NTT(int *s,int n) {
    
    
	for(int i = 1;i < n;i ++) {
    
    
		rev[i] = ((rev[i>>1] >> 1) | ((i&1) ? (n>>1):0));
		if(rev[i] < i) swap(s[rev[i]],s[i]);
	}
	om = qkpow(RM,(MOD-1)/n); xm[0] = 1;
	for(int k = 1;k < n;k ++) xm[k] = xm[k-1]*1ll*om % MOD;
	for(int k = 2,t = (n>>1);k <= n;k <<= 1,t >>= 1)
		for(int j = 0;j < n;j += k)
			for(int i = j,l = 0;i < j+(k>>1);i ++,l += t) {
    
    
				int A = s[i],B = s[i+(k>>1)];
				s[i] = (A + xm[l]*1ll*B%MOD) % MOD, s[i+(k>>1)] = (A +MOD- xm[l]*1ll*B%MOD) % MOD;
			}
	return ;
}
void INTT(int *s,int n) {
    
    
	for(int i = 1;i < n;i ++) {
    
    
		rev[i] = ((rev[i>>1] >> 1) | ((i&1) ? (n>>1):0));
		if(rev[i] < i) swap(s[rev[i]],s[i]);
	}
	om = qkpow(qkpow(RM,(MOD-1)/n),MOD-2); xm[0] = 1;
	for(int k = 1;k < n;k ++) xm[k] = xm[k-1]*1ll*om % MOD;
	for(int k = 2,t = (n>>1);k <= n;k <<= 1,t >>= 1)
		for(int j = 0;j < n;j += k)
			for(int i = j,l = 0;i < j+(k>>1);i ++,l += t) {
    
    
				int A = s[i],B = s[i+(k>>1)];
				s[i] = (A + xm[l]*1ll*B%MOD) % MOD, s[i+(k>>1)] = (A +MOD- xm[l]*1ll*B%MOD) % MOD;
			}
	int invn = qkpow(n,MOD-2);
	for(int i = 0;i <= n;i ++) s[i] = s[i] *1ll* invn % MOD;
	return ;
}
//------------------------NTT End
int inv[MAXN];
int init_inv() {
    
       // 预处理逆元
	inv[0]=inv[1]=1;
	for(int i=2;i<=MAXN-2;i++)
		inv[i] = (MOD-inv[MOD%i]) *1ll* (MOD/i) % MOD;
	return 0;
}
int useless_number = init_inv(); // completely useless
int po[40005];
map<int,int> mp;
int sqrt_mod(int x) {
    
     // 二次剩余
	int m = ceil(sqrt((DB)MOD));
	po[0] = 1; mp.clear();
	int pm = 1;
	for(int i = 1;i <= m;i ++) {
    
    
		po[i] = po[i-1] *3ll % MOD;
		pm = pm *3ll % MOD;
		mp[po[i]*1ll*x % MOD] = i;
	}
	int pa = 1,ct = 0,as,ans;
	for(int i = 1;i <= m;i ++) {
    
    
		pa = pa *1ll* pm % MOD; ct += m;
		if(as=mp[pa]) {
    
    
			ans = ct - as; break;
		}
	}
	int res = qkpow(3,ans/2);
	return min(res,MOD-res);
}
void polymul(int *A,int *B,int n) {
    
     // A *= B mod x^(n+1)
	int le = 1;
	while(le <= n*2) le <<= 1;
	for(int i = n+1;i <= le;i ++) A[i] = B[i] = 0;
	NTT(A,le);NTT(B,le);
	for(int i = 0;i <= le;i ++) A[i] = A[i]*1ll*B[i] % MOD,B[i]=0;
	INTT(A,le);for(int i = n+1;i <= le;i ++) A[i]=0;
}
void qiu_dao(int *s,int n) {
    
    
	for(int i = 0;i < n;i ++) s[i] = (1ll+i) * s[i+1] % MOD;s[n] = 0;
}
void ji_fen(int *s,int n) {
    
    
	for(int i = n+1;i > 0;i --) s[i] = s[i-1]*1ll*inv[i] % MOD;s[0] = 0;
}
int a_[MAXN<<2],b_[MAXN<<2];
void polyinv(int *s,int n) {
    
     // mod x^n
	for(int i = 0;i <= n;i ++) a_[i] = s[i],s[i]=0;
	s[0] = qkpow(a_[0],MOD-2);
	int le = 1;
	while(le < n) {
    
    
		le <<= 1;
		for(int i = 0;i < le;i ++) b_[i]=a_[i];
		NTT(b_,le<<1),NTT(s,le<<1);
		for(int i = 0;i <= (le<<1);i ++)
			s[i] = (2ll+MOD-b_[i]*1ll*s[i] % MOD) % MOD *1ll* s[i] % MOD,b_[i]=0;
		INTT(s,le<<1);
		for(int i = le;i <= (le<<1);i ++) s[i] = 0;
	}
	for(int i = n;i <= le;i ++) s[i] = 0;
	for(int i = 0;i <= n;i ++) a_[i] = 0; // tool cleared
	return ;
}
int c_[MAXN<<2];
void polyln(int *s,int n) {
    
     // mod x^n
	for(int i = 0;i < n;i ++) c_[i] = s[i];
	polyinv(s,n);qiu_dao(c_,n-1);
	polymul(s,c_,n-1); // c_ has been cleared here
	ji_fen(s,n-1); s[n] = 0;
}
int d_[MAXN<<2],e_[MAXN<<2];
void polyexp(int *s,int n) {
    
     // mod x^n
	for(int i = 0;i < n;i ++) d_[i] = s[i],s[i] = 0;
	s[0] = 1;int le = 1;
	while(le < n) {
    
    
		le <<= 1;
		for(int i = 0;i < le;i ++) e_[i] = s[i];
		polyln(e_,le);
		for(int i = 0;i < le;i ++) e_[i] = (d_[i]+MOD-e_[i]) % MOD;
		e_[0] = (e_[0]+1) % MOD;
		NTT(e_,le<<1);NTT(s,le<<1);
		for(int i = 0;i <= (le<<1);i ++)
			s[i] = e_[i]*1ll*s[i] % MOD,e_[i] = 0;
		INTT(s,le<<1);
		for(int i = le;i <= (le<<1);i ++) s[i] = 0;
	}
	for(int i = n;i <= le;i ++) s[i] = 0;
	for(int i = 0;i < n;i ++) d_[i] = 0;
	return ;
}
void polypow(int *s,int k,int n) {
    
     // mod x^n
	polyln(s,n);
	for(int i = 0;i < n;i ++) s[i] = s[i]*1ll*k % MOD;
	polyexp(s,n); return ;
}
int f_[MAXN<<2],g_[MAXN<<2],h_[MAXN<<2];
void polysqrt(int *s,int n) {
    
     // mod x^n
	for(int i = 0;i < n;i ++) f_[i] = s[i],s[i] = 0;
	s[0] = sqrt_mod(f_[0]);int le = 1;
	while(le < n) {
    
    
		le <<= 1;
		for(int i = 0;i < le;i ++) g_[i] = s[i],h_[i] = f_[i];
		polyinv(g_,le);
		NTT(g_,le<<1);NTT(h_,le<<1);
		for(int i = 0;i <= (le<<1);i ++) g_[i] = g_[i] *1ll* h_[i] % MOD,h_[i]=0;
		INTT(g_,le<<1);
		for(int i = 0;i < le;i ++)
			s[i] = (s[i]+g_[i]) % MOD *1ll*inv[2] % MOD;
		for(int i = 0;i <= (le<<1);i ++) g_[i] = 0;
	}
	for(int i = n;i <= le;i ++) s[i] = 0;
	for(int i = 0;i < n;i ++) f_[i] = 0;
	return ;
}
//-----------------------END----------------

练手题

多项式乘法逆
多项式除法
多项式对数函数（多项式 ln）
多项式指数函数（多项式 exp）
多项式快速幂
多项式开根
多项式开根（加强版）

挑战多项式

前面的都是模板题，没什么好说的，注意该清零的清零。

后面的挑战多项式有一点必须要注意，就是它的二次探测部分，我们知道满足 $x^2\equiv n(\mathrm{m}\mathrm{o}\mathrm{d}p)$ 的 $x$ 可以是 $x$ 也可以是 $p-x$ （即 $-x$）（但这和原根跑大步小步跑出的是唯一解并不矛盾），题面中说的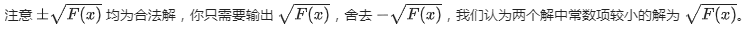
意思就是在 $x$ 和 $mod-x$ 中我们要选更小的一个作为二次剩余的结果，更小是指取模意义下的值更小。

进阶题

多项式最小共倍式的一道题。

题意

给一个 $N\ast N$ 矩阵 $A$ ，求次数最小的多项式 $f$ ，满足 $f(A)=0$（这里的常数可以看成是单位矩阵的常数倍），给定模数 $P$ ，求出一个最高次项系数为 1 的符合题意的多项式。保证有解。

$N\le 70$

做法

如果把 $A$ 的 1~N×N 次方都求出来，对于矩阵的每个位置可以列出一个方程，总共 N×N 个 N×N 元方程，那么就可以做高斯消元，但是这样是 $O(N^6)$ 的过不了。

令 $f(A)=f_0+f_{1}A+f_2{A}^2+f_3{A}^3+...=0$ ，那么对于任意一个 1×N 的向量矩阵 B，肯定满足 $B\ast f(A)=f_{0}B+f_1(BA)+f_2(B{A}^2)+f_3(B{A}^3)+...=0$ ，这里的 0 就不是单位矩阵了，而是一个 1×N 的全 0 矩阵。

那么我们把矩阵 A 的 1~N 次方都在前面(矩阵乘法没有交换律)乘上一个矩阵 B ，这样就不用列这么多方程，而是只用列 N 个方程，N 个未知数，因为矩阵都变成 1×N 的了。

我们随机一个向量矩阵 B 乘上去，用高斯消元求出的多项式大概率是对的，但不一定，所以我们多随机几个矩阵 B ，把求出来的多项式取最小共倍式，就可以基本保证正确了。