机器人学回炉重造（2-3）：基本雅可比矩阵与其他雅可比矩阵

基本雅可比矩阵

定义

用笛卡尔坐标描述线速度（linear velocity）和角速度（angular velocity）、以机械臂的基坐标系（Base frame或frame{0}) 作为参照系来描述end effector速度所求得的雅可比矩阵，称为基本雅可比矩阵；其它所有表示方法（比如将笛卡尔坐标改为柱坐标、球坐标；角度改为欧拉角或四元数quaternion等）都可由这个基本雅可比矩阵转换得到。

求法

机器人学回炉重造（2-2）：雅可比矩阵的求法——矢量积法、微分变换法、Manipulator Jacobian（Jacobian for short）

其他雅可比矩阵

定义

其他雅可比矩阵就是指末端通过柱坐标、球坐标表示，以及姿态通过欧拉角、RPY角或者四元数表示进而计算得到的雅可比矩阵。

求法

得到基本雅可比矩阵后，要求其它形式的雅可比矩阵都不是问题，只需要乘一个转换矩阵就可以了。
比如说，如果你的end effector位置是由柱坐标表示的，即(ρ,θ, z)，而柱坐标转换为笛卡尔坐标是：

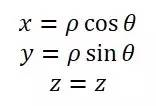
那么转换矩阵Ep（这里的p表示position）就由笛卡尔坐标对柱坐标的向量求导得出：

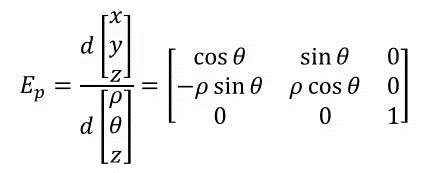
而新的雅可比矩阵的上半部分就等于几何雅可比矩阵的Jv左乘上这个Ep。对于旋转也类似。

补充：几何雅可比与解析雅可比

有一些书上描述的是“几何雅可比矩阵”与“解析雅可比矩阵”：

• 几何雅可比是根据几何方法进行雅可比矩阵计算，可以确定每个关节速度对末端执行器线速度与角速度分量的作用；
• 解析雅可比是通过正运动学方程对关节变量的微分来计算雅可比矩阵。

其中，解析雅可比由于末端姿态角表示方式的不同（欧拉角、RPY角表示等），会导致末端执行器相对于基坐标系{0}的角速度$\omega$并不等于姿态角的导数。