原论文链接:VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator
参考:崔华坤-《VINS论文推导及代码解析》与 高翔-《视觉SLAM十四讲》
整理了 VINS-Mono 论文中 关于 IMU 预积分公式及协方差、雅可比矩阵传递的推导。
目录
1. IMU 原始加速度和角加速度
IMU 原始加速度和角加速度(相对于IMU/本体 坐标系)表示如下:
(1)
a ^ t = a t + b a t + R w t g w + n a ω ^ t = ω t + b w t + n w \begin{aligned} &\hat{\mathbf{a}}_{t}=\mathbf{a}_{t}+\mathbf{b}_{a_{t}}+\mathbf{R}_{w}^{t} \mathbf{g}^{w}+\mathbf{n}_{a} \\ &\hat{\boldsymbol{\omega}}_{t}=\boldsymbol{\omega}_{t}+\mathbf{b}_{w_{t}}+\mathbf{n}_{w} \end{aligned} a^t=at+bat+Rwtgw+naω^t=ωt+bwt+nw
(1)式中
n a ∼ N ( 0 , σ a 2 ) , n w ∼ N ( 0 , σ w 2 ) b ˙ a t = n b a , n b a ∼ N ( 0 , σ b a 2 ) b ˙ w t = n b w , n b w ∼ N ( 0 , σ b w 2 ) \begin{aligned} &\mathbf{n}_{a} \sim \mathcal{N}\left(\mathbf{0}, \sigma_{a}^{2}\right), \mathbf{n}_{w} \sim \mathcal{N}\left(\mathbf{0}, \sigma_{w}^{2}\right) \\ &\dot{\mathbf{b}}_{a_{t}}=\mathbf{n}_{b_{a}}, \mathbf{n}_{b_{a}} \sim \mathcal{N}\left(\mathbf{0}, \sigma_{b_{a}}^{2}\right) \\ &\dot{\mathbf{b}}_{w_{t}}=\mathbf{n}_{b_{w}}, \mathbf{n}_{b_{w}} \sim \mathcal{N}\left(\mathbf{0}, \sigma_{b_{w}}^{2}\right) \end{aligned} na∼N(0,σa2),nw∼N(0,σw2)b˙at=nba,nba∼N(0,σba2)b˙wt=nbw,nbw∼N(0,σbw2)
2. 当前时刻 PVQ 的连续形式
定义采集到的连续两帧图像为 b k b_k bk 和 b k + 1 b_{k+1} bk+1,则在时间区间 [ t k , t k + 1 ] [t_k, t_{k+1}] [tk,tk+1] 内对位置 P,速度 V 和四元数表示的旋转 Q 进行积分的公式如下(得到结果的参考坐标系为世界坐标系):
(23)
p b k + 1 w = p b k w + v b k w Δ t k + ∬ t ∈ [ t k , t k + 1 ] ( R t w ( a ^ t − b a t − n a ) − g w ) d t 2 v b k + 1 w = v b k w + ∫ t ∈ [ t k , t k + 1 ] ( R t w ( a ^ t − b a t − n a ) − g w ) d t q b k + 1 w = q b k w ⊗ ∫ t ∈ [ t k , t k + 1 ] 1 2 Ω ( ω ^ t − b w t − n w ) q t b k d t \begin{aligned} \mathbf{p}_{b_{k+1}}^{w}&=\mathbf{p}_{b_{k}}^{w} +\mathbf{v}_{b_{k}}^{w} \Delta t_{k} +\iint_{t \in\left[t_{k}, t_{k+1}\right]}\left(\mathbf{R}_{t}^{w}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{a_{t}}-\mathbf{n}_{a}\right)-\mathbf{g}^{w}\right) d t^{2} \\ \mathbf{v}_{b_{k+1}}^{w}&=\mathbf{v}_{b_{k}}^{w} +\int_{t \in\left[t_{k}, t_{k+1}\right]}\left(\mathbf{R}_{t}^{w}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{a_{t}}-\mathbf{n}_{a}\right)-\mathbf{g}^{w}\right) d t \\ \mathbf{q}_{b_{k+1}}^{w}&=\mathbf{q}_{b_{k}}^{w} \otimes \int_{t \in\left[t_{k}, t_{k+1}\right]} \frac{1}{2} \Omega\left(\hat{\boldsymbol{\omega}}_{t}-\mathbf{b}_{w_{t}}-\mathbf{n}_{w}\right) \mathbf{q}_{t}^{b_{k}} d t \end{aligned} pbk+1wvbk+1wqbk+1w=pbkw+vbkwΔtk+∬t∈[tk,tk+1](Rtw(a^t−bat−na)−gw)dt2=vbkw+∫t∈[tk,tk+1](Rtw(a^t−bat−na)−gw)dt=qbkw⊗∫t∈[tk,tk+1]21Ω(ω^t−bwt−nw)qtbkdt
where
(24)
Ω ( ω ) = [ − ⌊ ω ⌋ × ω − ω T 0 ] , ⌊ ω ⌋ × = [ 0 − ω z ω y ω z 0 − ω x − ω y ω x 0 ] \boldsymbol{\Omega}(\boldsymbol{\omega})=\left[\begin{array}{cc} -\lfloor\boldsymbol{\omega}\rfloor_{\times} & \boldsymbol{\omega} \\ -\boldsymbol{\omega}^{T} & 0 \end{array}\right],\lfloor\boldsymbol{\omega}\rfloor_{\times}=\left[\begin{array}{ccc} 0 & -\omega_{z} & \omega_{y} \\ \omega_{z} & 0 & -\omega_{x} \\ -\omega_{y} & \omega_{x} & 0 \end{array}\right] Ω(ω)=[−⌊ω⌋×−ωTω0],⌊ω⌋×=⎣⎡0ωz−ωy−ωz0ωxωy−ωx0⎦⎤
R t w R_t^w Rtw 表示 t 时刻 IMU/本体 坐标系 到 世界坐标系的旋转矩阵;
q t b k q_t^{b_k} qtbk 表示 t 时刻 IMU/本体 坐标系 相对于采集 b k b_k bk的时刻的 IMU/本体 坐标系 的旋转(四元数形式)。
q b k w q_{b_k}^w qbkw 表示 采集 b k b_k bk的时刻的IMU坐标系 相对于 世界坐标系 的旋转(四元数形式)。论文中四元数向量的实部是向量最后一个元素。
四元数的积分涉及到四元数求导、四元数与旋转向量的转换等的知识。
四元数求导推导请看文章后半部分。
3. 两帧之间 PVQ 增量的连续形式
因为上述公式的积分项存在 R t w R_t^w Rtw 或者 q q q,IMU状态传递需要知道 b k b_k bk 时刻的 PVQ,优化算法每次对状态优化后都需要重新传递 IMU 的测量,降低了处理速度。
所以引出了预积分。
将参考坐标系从世界坐标系改为 b k b_k bk 的 IMU/本体 坐标系,Q、V等式两边同时左乘 R w b k R_w^{b_k} Rwbk,Q等式左右两边同时左乘 q w b k q_w^{b_k} qwbk:
(25)
R w b k p b k + 1 w = R w b k ( p b k w + v b k w Δ t k − 1 2 g w Δ t k 2 ) + α b k + 1 b k R w b k v b k + 1 w = R w b k ( v b k w − g w Δ t k ) + β b k + 1 b k q w b k ⊗ q b k + 1 w = γ b k + 1 b k \begin{aligned} \mathbf{R}_{w}^{b_{k}} \mathbf{p}_{b_{k+1}}^{w} &=\mathbf{R}_{w}^{b_{k}}\left(\mathbf{p}_{b_{k}}^{w}+\mathbf{v}_{b_{k}}^{w} \Delta t_{k}-\frac{1}{2} \mathbf{g}^{w} \Delta t_{k}^{2}\right)+\alpha_{b_{k+1}}^{b_{k}} \\ \mathbf{R}_{w}^{b_{k}} \mathbf{v}_{b_{k+1}}^{w} &=\mathbf{R}_{w}^{b_{k}}\left(\mathbf{v}_{b_{k}}^{w}-\mathbf{g}^{w} \Delta t_{k}\right)+\boldsymbol{\beta}_{b_{k+1}}^{b_{k}} \\ \mathbf{q}_{w}^{b_{k}} \otimes \mathbf{q}_{b_{k+1}}^{w} &=\boldsymbol{\gamma}_{b_{k+1}}^{b_{k}} \end{aligned} Rwbkpbk+1wRwbkvbk+1wqwbk⊗qbk+1w=Rwbk(pbkw+vbkwΔtk−21gwΔtk2)+αbk+1bk=Rwbk(vbkw−gwΔtk)+βbk+1bk=γbk+1bk
where
(26)
α b k + 1 b k = ∬ t ∈ [ t k , t k + 1 ] R t b k ( a ^ t − b a t − n a ) d t 2 β b k + 1 b k = ∫ t ∈ [ t k , t k + 1 ] R t b k ( a ^ t − b a t − n a ) d t γ b k + 1 b k = ∫ t ∈ [ t k , t k + 1 ] 1 2 Ω ( ω ^ t − b w t − n w ) γ t b k d t . \begin{aligned} \boldsymbol{\alpha}_{b_{k+1}}^{b_{k}} &=\iint_{t \in\left[t_{k}, t_{k+1}\right]} \mathbf{R}_{t}^{b_{k}}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{a_{t}}-\mathbf{n}_{a}\right) d t^{2} \\ \boldsymbol{\beta}_{b_{k+1}}^{b_{k}} &=\int_{t \in\left[t_{k}, t_{k+1}\right]} \mathbf{R}_{t}^{b_{k}}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{a_{t}}-\mathbf{n}_{a}\right) d t \\ \boldsymbol{\gamma}_{b_{k+1}}^{b_{k}} &=\int_{t \in\left[t_{k}, t_{k+1}\right]} \frac{1}{2} \boldsymbol{\Omega}\left(\hat{\boldsymbol{\omega}}_{t}-\mathbf{b}_{w_{t}}-\mathbf{n}_{w}\right) \boldsymbol{\gamma}_{t}^{b_{k}} d t . \end{aligned} αbk+1bkβbk+1bkγbk+1bk=∬t∈[tk,tk+1]Rtbk(a^t−bat−na)dt2=∫t∈[tk,tk+1]Rtbk(a^t−bat−na)dt=∫t∈[tk,tk+1]21Ω(ω^t−bwt−nw)γtbkdt.
其中 (26) 就是3个预积分项,只有这三个项存在 a t ^ \hat{a_t} at^ 或者 w t ^ \hat{w_t} wt^。
4. 两帧之间 PVQ 增量的零阶保持法离散形式
讨论离散情况。
论文给出了零阶保持离散化方法:
(27)
α ^ i + 1 b k = α ^ i b k + β ^ i b k δ t + 1 2 R ( γ ^ i b k ) ( a ^ i − b a i ) δ t 2 β ^ i + 1 b k = β ^ i b k + R ( γ ^ i b k ) ( a ^ i − b a i ) δ t γ ^ i + 1 b k = γ ^ i b k ⊗ [ 1 1 2 ( ω ^ i − b w i ) δ t ] \begin{aligned} &\hat{\boldsymbol{\alpha}}_{i+1}^{b_{k}}=\hat{\boldsymbol{\alpha}}_{i}^{b_{k}}+\hat{\boldsymbol{\beta}}_{i}^{b_{k}} \delta t+\frac{1}{2} \mathbf{R}\left(\hat{\gamma}_{i}^{b_{k}}\right)\left(\hat{\mathbf{a}}_{i}-\mathbf{b}_{a_{i}}\right) \delta t^{2} \\ &\hat{\boldsymbol{\beta}}_{i+1}^{b_{k}}=\hat{\boldsymbol{\beta}}_{i}^{b_{k}}+\mathbf{R}\left(\hat{\gamma}_{i}^{b_{k}}\right)\left(\hat{a}_{i}-\mathbf{b}_{a_{i}}\right) \delta t \\ &\hat{\gamma}_{i+1}^{b_{k}}=\hat{\gamma}_{i}^{b_{k}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2}\left(\hat{\omega}_{i}-\mathbf{b}_{w_{i}}\right) \delta t \end{array}\right] \end{aligned} α^i+1bk=α^ibk+β^ibkδt+21R(γ^ibk)(a^i−bai)δt2β^i+1bk=β^ibk+R(γ^ibk)(a^i−bai)δtγ^i+1bk=γ^ibk⊗[121(ω^i−bwi)δt]
其中 i 表示在时间区间 [ t k , t k + 1 ] [t_k, t_{k+1}] [tk,tk+1] 内 IMU 的第 i 个测量, δ t \delta t δt 为 i~i+1之间的时间长度。
5. IMU 误差项导数
IMU 的积分值是有误差的,对误差进行分析。
将 四元数 γ \gamma γ 的误差定义为其均值附近的扰动:
(28)
γ t b k ≈ γ ^ t b k ⊗ [ 1 1 2 δ θ t b k ] \gamma_{t}^{b_{k}} \approx \hat{\gamma}_{t}^{b_{k}} \otimes\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \theta_{t}^{b_{k}} \end{array}\right] γtbk≈γ^tbk⊗[121δθtbk]
δ θ t b k \delta \theta_t^{b_k} δθtbk 是 t 时刻 IMU/本体 坐标系 相对于采集 b k b_k bk的时刻的 IMU/本体 坐标系 的旋转 3D 小扰动。
连续形式 IMU 误差项导数(误差动力学方程):
(29)
[ δ α ˙ t b k δ β ˙ t b k δ θ ˙ t b k δ b ˙ a t δ b ˙ w t ] = [ 0 I 0 0 0 0 0 0 − R t b k ⌊ a ^ t − b a t ⌋ × − R t b k 0 0 0 0 − ⌊ ω ^ t − b w t ⌋ × 0 − I 0 0 0 0 0 0 0 0 0 0 0 ] [ δ α t b k δ β t b k δ θ t b k δ b a t δ b w t ] + [ 0 0 0 0 − R t b k 0 0 0 0 − I 0 0 0 0 I 0 0 0 0 I ] [ n a n w n b a n b w ] = F t δ z t b k + G t n t . \begin{aligned} \left[\begin{array}{c} \delta \dot{\boldsymbol{\alpha}}_{t}^{b_{k}} \\ \delta \dot{\boldsymbol{\beta}}_{t}^{b_{k}} \\ \delta \dot{\boldsymbol{\theta}}_{t}^{b_{k}} \\ \delta \dot{\mathbf{b}}_{a_{t}} \\ \delta \dot{\mathbf{b}}_{w_{t}} \end{array}\right]=&\left[\begin{array}{cccccc} 0 & \mathbf{I} & 0 & 0 & 0 &0\\ 0 & 0 & -\mathbf{R}_{t}^{b_{k}}\left\lfloor\hat{\mathbf{a}}_{t}-\mathbf{b}_{a_{t}}\right\rfloor_{\times} & -\mathbf{R}_{t}^{b_{k}} & 0 &0\\ 0 & 0 & -\left\lfloor\hat{\boldsymbol{\omega}}_{t}\right. & \left.-\mathbf{b}_{w_{t}}\right\rfloor_{\times} & 0 & -\mathbf{I} \\ 0 & 0 & 0 & 0 & 0 &0\\ 0 & 0 & & 0 & 0 & 0 \end{array}\right]\left[\begin{array}{c} \delta \boldsymbol{\alpha}_{t}^{b_{k}} \\ \delta \boldsymbol{\beta}_{t}^{b_{k}} \\ \delta \boldsymbol{\theta}_{t}^{b_{k}} \\ \delta \mathbf{b}_{a_{t}} \\ \delta \mathbf{b}_{w_{t}} \end{array}\right] +\left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ -\mathbf{R}_{t}^{b_{k}} & 0 & 0 & 0 \\ 0 & -\mathbf{I} & 0 & 0 \\ 0 & 0 & \mathbf{I} & 0 \\ 0 & 0 & 0 & \mathbf{I} \end{array}\right]\left[\begin{array}{c} \mathbf{n}_{a} \\ \mathbf{n}_{w} \\ \mathbf{n}_{b_{a}} \\ \mathbf{n}_{b_{w}} \end{array}\right]=\mathbf{F}_{t} \delta \mathbf{z}_{t}^{b_{k}}+\mathbf{G}_{t} \mathbf{n}_{t} . \end{aligned} ⎣⎢⎢⎢⎢⎢⎡δα˙tbkδβ˙tbkδθ˙tbkδb˙atδb˙wt⎦⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡00000I00000−Rtbk⌊a^t−bat⌋×−⌊ω^t00−Rtbk−bwt⌋×000000000−I00⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡δαtbkδβtbkδθtbkδbatδbwt⎦⎥⎥⎥⎥⎤+⎣⎢⎢⎢⎢⎡0−Rtbk00000−I00000I00000I⎦⎥⎥⎥⎥⎤⎣⎢⎢⎡nanwnbanbw⎦⎥⎥⎤=Ftδztbk+Gtnt.
F t 15 × 15 , G t 15 × 12 , δ z t b k 15 × 1 , n t 12 × 1 F_{t}{ }^{15 \times 15}, G_{t}{ }^{15 \times 12}, \delta z_{t}^{b_{k}^{15 \times 1}}, n_{t}{ }^{12 \times 1} Ft15×15,Gt15×12,δztbk15×1,nt12×1
对其中 δ β ˙ t b k \delta \dot{\beta}_t^{b_k} δβ˙tbk 和 δ θ ˙ t b k \delta \dot{\theta}_t^{b_k} δθ˙tbk 进行推导。
δ β ˙ t b k \delta \dot{\beta}_t^{b_k} δβ˙tbk 的推导:
引入两个概念:true 和 nominal,其中:
true:真实测量值,包含了噪声
nominal:无噪声的理论值
则

其中第二步中 e x p ( δ θ exp(\delta \theta exp(δθ^ ) ) ) 是对 R t b k R_t^{b_k} Rtbk 的扰动,涉及到 李群与李代数 方面的知识,《十四讲》中有相关内容。
δ β ˙ t b k \delta \dot{\beta}_t^{b_k} δβ˙tbk 简写成 δ β ˙ \delta \dot{\beta} δβ˙:
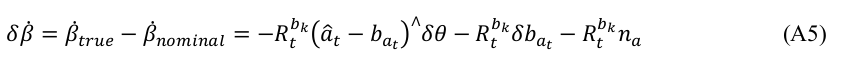
δ θ ˙ t b k \delta \dot{\theta}_t^{b_k} δθ˙tbk 的推导:
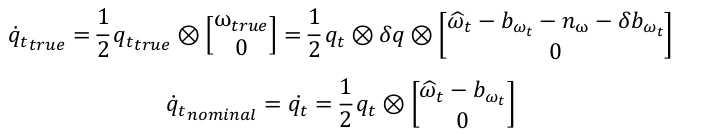
类似的, δ q \delta q δq 是对 q t q_t qt 的扰动。
根据导数的性质(乘法的求导法则),又有:
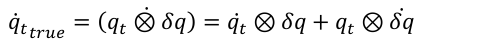
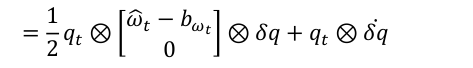
综合上式,可得等式如下( δ θ ˙ t b k \delta \dot{\theta}_t^{b_k} δθ˙tbk 简写成 δ θ ˙ \delta \dot{\theta} δθ˙:):

上式左侧也可以写成:

q = [ k ^ s i n θ 2 , c o s θ 2 ] T ≈ [ θ 2 , 1 ] q = [\hat{k}sin\frac{\theta}{2}, cos\frac{\theta}{2}]^T \approx [\frac{\theta}{2}, 1] q=[k^sin2θ,cos2θ]T≈[2θ,1]
δ q ˙ = [ δ θ ˙ 2 , 0 ] T \delta \dot q = [\frac{\delta\dot\theta}{2}, 0]^T δq˙=[2δθ˙,0]T
6. 噪声协方差矩阵传递公式
将 式(29) 简写成: δ z ˙ t b k = F t δ z t b k + G t n t \delta \dot{z}_{t}^{b_{k}}=F_{t} \delta z_{t}^{b_{k}}+G_{t} n_{t} δz˙tbk=Ftδztbk+Gtnt
则(均值预测公式):
δ z ˙ t b k = lim δ t → 0 δ z t + δ t b k − δ z t b k δ t δ z t + δ t b k = δ z t b k + δ z ˙ t b k δ t = ( I + F t δ t ) δ z t b k + ( G t δ t ) n t = F δ z t b k + V n t \begin{aligned} \delta \dot{z}_{t}^{b_{k}} &=\lim _{\delta t \rightarrow 0} \frac{\delta z_{t+\delta t}^{b_{k}}-\delta z_{t}^{b_{k}}}{\delta t} \\ \delta z_{t+\delta t}^{b_{k}} &=\delta z_{t}^{b_{k}}+\delta \dot{z}_{t}^{b_{k}} \delta t=\left(\mathrm{I}+F_{t} \delta t\right) \delta z_{t}^{b_{k}}+\left(G_{t} \delta t\right) n_{t} \\ &=F \delta z_{t}^{b_{k}}+V n_{t} \end{aligned} δz˙tbkδzt+δtbk=δt→0limδtδzt+δtbk−δztbk=δztbk+δz˙tbkδt=(I+Ftδt)δztbk+(Gtδt)nt=Fδztbk+Vnt
上式中 F = I + F t δ t F= I +F_{t} \delta t F=I+Ftδt , V = G t δ t V=G_{t} \delta t V=Gtδt 。
上式恰好给出了 EKF 一般对非线性系统线性化的过程,这里的意义是表示下一个时刻的 IMU 测量误差与上一个时刻的成线性关系。
零阶保持法中, F t \mathbf{F}_{t} Ft 在积分周期内为常数,所以
F d = exp ( F t δ t ) ≈ I + F t δ t \mathbf{F}_{d}=\exp \left(\mathbf{F}_{t} \delta t\right)\approx \mathbf{I}+\mathbf{F}_{t} \delta t Fd=exp(Ftδt)≈I+Ftδt
由连续形式噪声协方差矩阵: Q t = diag ( σ a 2 , σ w 2 , σ b a 2 , σ b w 2 ) \mathbf{Q}_{t}=\operatorname{diag}\left(\sigma_{a}^{2}, \sigma_{w}^{2}, \sigma_{b_{a}}^{2}, \sigma_{b_{w}}^{2}\right) Qt=diag(σa2,σw2,σba2,σbw2)
得到离散形式噪声协方差矩阵:
(30)
Q d = ∫ 0 δ t F d ( τ ) G t Q t G t T F d ( τ ) T = δ t F d G t Q t G t T F d T ≈ δ t G t Q t G t T \begin{aligned} \mathbf{Q}_{d} &=\int_{0}^{\delta t} \mathbf{F}_{d}(\tau) \mathbf{G}_{t} \mathbf{Q}_{t} \mathbf{G}_{t}^{T} \mathbf{F}_{d}(\tau)^{T} \\ &=\delta t \mathbf{F}_{d} \mathbf{G}_{t} \mathbf{Q}_{t} \mathbf{G}_{t}^{T} \mathbf{F}_{d}^{T} \\ & \approx \delta t \mathbf{G}_{t} \mathbf{Q}_{t} \mathbf{G}_{t}^{T} \end{aligned} Qd=∫0δtFd(τ)GtQtGtTFd(τ)T=δtFdGtQtGtTFdT≈δtGtQtGtT
协方差预测公式:
原论文
(31)
P t + δ t b k = ( I + F t δ t ) P t b k ( I + F t δ t ) T + δ t G t Q t G t T , t ∈ [ k , k + 1 ] \begin{array}{r} \mathbf{P}_{t+\delta t}^{b_{k}}=\left(\mathbf{I}+\mathbf{F}_{t} \delta t\right) \mathbf{P}_{t}^{b_{k}}\left(\mathbf{I}+\mathbf{F}_{t} \delta t\right)^{T}+\delta t \mathbf{G}_{t} \mathbf{Q}_{t} \mathbf{G}_{t}^{T}, \quad t \in[k, k+1] \end{array} Pt+δtbk=(I+Ftδt)Ptbk(I+Ftδt)T+δtGtQtGtT,t∈[k,k+1]
崔华坤论文推导
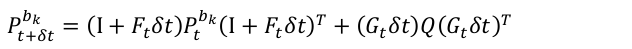
初始值 P b k b k = 0 \mathbf{P}_{b_{k}}^{b_{k}}=0 Pbkbk=0
7. 误差项的 Jacobian 矩阵传递公式 和 bias 的一阶近似
根据均值预测公式,也可以写出误差项的 Jacobian 矩阵的迭代公式:
J t + δ t = ( I + F t δ t ) J t , t ∈ [ k , k + 1 ] \mathbf{J}_{t+\delta t}=\left(\mathbf{I}+\mathbf{F}_{t} \delta t\right) \mathbf{J}_{t}, \quad t \in[k, k+1] Jt+δt=(I+Ftδt)Jt,t∈[k,k+1]
初始值 J b k = I \mathbf{J}_{b_{k}}=\mathbf{I} Jbk=I
式(26) 关于 bias 的一阶近似如下:
(33)
α b k + 1 b k ≈ α ^ b k + 1 b k + J b a α δ b a k + J b w α δ b w k β b k + 1 b k ≈ β ^ b k + 1 b k + J b a β δ b a k + J b w β δ b w k γ b k + 1 b k ≈ γ ^ b k + 1 b k ⊗ [ 1 1 2 J b w γ δ b w k ] \begin{aligned} \boldsymbol{\alpha}_{b_{k+1}}^{b_{k}} & \approx \hat{\boldsymbol{\alpha}}_{b_{k+1}}^{b_{k}}+\mathbf{J}_{b_{a}}^{\alpha} \delta \mathbf{b}_{a_{k}}+\mathbf{J}_{b_{w}}^{\alpha} \delta \mathbf{b}_{w_{k}} \\ \boldsymbol{\beta}_{b_{k+1}}^{b_{k}} & \approx \hat{\boldsymbol{\beta}}_{b_{k+1}}^{b_{k}}+\mathbf{J}_{b_{a}}^{\beta} \delta \mathbf{b}_{a_{k}}+\mathbf{J}_{b_{w}}^{\beta} \delta \mathbf{b}_{w_{k}} \\ \gamma_{b_{k+1}}^{b_{k}} & \approx \hat{\boldsymbol{\gamma}}_{b_{k+1}}^{b_{k}} \otimes\left[\begin{array}{cc} 1 \\ \frac{1}{2} \mathbf{J}_{b_{w}}^{\gamma} \delta \mathbf{b}_{w_{k}} \end{array}\right] \end{aligned} αbk+1bkβbk+1bkγbk+1bk≈α^bk+1bk+Jbaαδbak+Jbwαδbwk≈β^bk+1bk+Jbaβδbak+Jbwβδbwk≈γ^bk+1bk⊗[121Jbwγδbwk]
其中 J b a α \mathbf{J}_{b_{a}}^{\alpha} Jbaα 是 J b k + 1 \mathbf{J}_{b_{k+1}} Jbk+1 的关于 δ α b k + 1 b k / δ b a k {\delta \boldsymbol{\alpha}_{b_{k+1}}^{b_k} }/{\delta \mathbf{b}_{a_k}} δαbk+1bk/δbak 的子块。
J b w α , J b a β , J b w β , J b w γ \mathbf{J}_{b_{w}}^{\alpha}, \mathbf{J}_{b_{a}}^{\beta}, \mathbf{J}_{b_{w}}^{\beta}, \mathbf{J}_{b_{w}}^{\gamma} Jbwα,Jbaβ,Jbwβ,Jbwγ 类似。
当 bias 被优化改变时,使用上式调整预积分而不是重新积分。
8. 协方差为 P b k + 1 b k \mathbf{P}_{b_{k+1}}^{b_{k}} Pbk+1bk 下 IMU 测量模型:
[ α ^ b k + 1 b k β ^ b k + 1 b k γ ^ b k + 1 b k 0 0 ] = [ R w b k ( p b k + 1 w − p b k w + 1 2 g w Δ t k 2 − v b k w Δ t k ) R w b k ( v b k + 1 w + g w Δ t k − v b k w ) q b k w − 1 ⊗ q b k + 1 w b a b k + 1 − b a b k b w b k + 1 − b w b k ] \left[\begin{array}{c} \hat{\boldsymbol{\alpha}}_{b_{k+1}}^{b_{k}} \\ \hat{\boldsymbol{\beta}}_{b_{k+1}}^{b_{k}} \\ \hat{\boldsymbol{\gamma}}_{b_{k+1}}^{b_{k}} \\ \mathbf{0} \\ \mathbf{0} \end{array}\right]=\left[\begin{array}{c} \mathbf{R}_{w}^{b_{k}}\left(\mathbf{p}_{b_{k+1}}^{w}-\mathbf{p}_{b_{k}}^{w}+\frac{1}{2} \mathbf{g}^{w} \Delta t_{k}^{2}-\mathbf{v}_{b_{k}}^{w} \Delta t_{k}\right) \\ \mathbf{R}_{w}^{b_{k}}\left(\mathbf{v}_{b_{k+1}}^{w}+\mathbf{g}^{w} \Delta t_{k}-\mathbf{v}_{b_{k}}^{w}\right) \\ \mathbf{q}_{b_{k}}^{w^{-1}} \otimes \mathbf{q}_{b_{k+1}}^{w} \\ \mathbf{b}_{a b_{k+1}}-\mathbf{b}_{a b_{k}} \\ \mathbf{b}_{w b_{k+1}}-\mathbf{b}_{w b_{k}} \end{array}\right] ⎣⎢⎢⎢⎢⎢⎡α^bk+1bkβ^bk+1bkγ^bk+1bk00⎦⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎡Rwbk(pbk+1w−pbkw+21gwΔtk2−vbkwΔtk)Rwbk(vbk+1w+gwΔtk−vbkw)qbkw−1⊗qbk+1wbabk+1−babkbwbk+1−bwbk⎦⎥⎥⎥⎥⎥⎥⎤
----------------附:四元数求导----------------
四元数乘法:
设 q a = x a i + y a j + z a k + s a , q b = x b i + y b j + z b k + s b q_a = x_a i+ y_a j+ z_ak + s_a, q_b = x_b i+ y_b j+ z_bk + s_b qa=xai+yaj+zak+sa,qb=xbi+ybj+zbk+sb,令 ⊗ 表示四元数乘法运算符。
由虚部满足的关系式:
i 2 = j 2 = k 2 = − 1 i j = k , j i = − k j k = i , k j = − i k i = j , i k = − j i^2 = j^2 = k^2 = -1\\ ij = k, ji = -k\\ jk = i, kj = -i\\ ki = j, ik = -j i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−j
计算:
q a ⊗ q b = ( s a x b + x a s b + y a z b − z a y b ) i + ( s a y b + x a z b + y a s b − z a x b ) j + ( s a z b + x a y b + y a x b − z a s b ) k + s a s b − x a x b − y a y b − z a z b \begin{aligned} q_a⊗q_b &= (s_ax_b + x_as_b + y_az_b - z_ay_b)i\\ &+(s_ay_b + x_az_b + y_as_b - z_ax_b)j\\ &+(s_az_b + x_ay_b + y_ax_b - z_as_b)k\\ &+ s_as_b - x_ax_b - y_ay_b - z_az_b\\ \end{aligned} qa⊗qb=(saxb+xasb+yazb−zayb)i+(sayb+xazb+yasb−zaxb)j+(sazb+xayb+yaxb−zasb)k+sasb−xaxb−yayb−zazb
引入左乘和右乘符号,写成矩阵乘法形式:

令 q = [ x y z s ] T = [ w T s ] T q = [x \; y \; z \; s]^T = [w^T \; s]^T q=[xyzs]T=[wTs]T,有
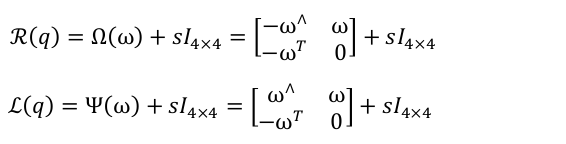
其中 ^ 为反对称符号(见《十四讲》 P43)。
四元数的导数推导:


k ^ θ \hat{k}\theta k^θ 是旋转向量。这里最后一行的 θ \theta θ 是个三维向量。
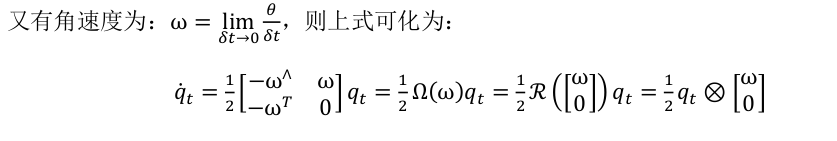
感觉最后两行推导不太正确。
或许可以解释为旋转向量对时间求导为角速度?