题目:
62、不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
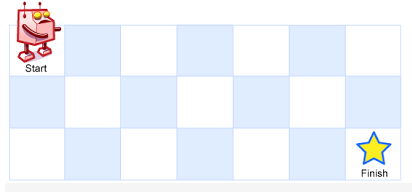
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 10^9
题解思路:
思路与算法
我们用 f(i, j) 表示从左上角走到 (i, j) 的路径数量,其中 i 和 j 的范围分别是 [0, m) 和 [0, n)。
由于我们每一步只能从向下或者向右移动一步,因此要想走到 (i, j),如果向下走一步,那么会从 (i-1, j) 走过来;如果向右走一步,那么会从 (i, j-1) 走过来。因此我们可以写出动态规划转移方程:
f(i, j) = f(i-1, j) + f(i, j-1)
需要注意的是,如果 i=0,那么 f(i-1,j) 并不是一个满足要求的状态,我们需要忽略这一项;同理,如果 j=0,那么 f(i,j-1) 并不是一个满足要求的状态,我们需要忽略这一项。
初始条件为 f(0,0)=1,即从左上角走到左上角有一种方法。
最终的答案即为 f(m-1,n-1)。
细节
为了方便代码编写,我们可以将所有的 f(0, j) 以及 f(i,0) 都设置为边界条件,它们的值均为 1。
题解python代码:
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
f = [[1] * n] + [[1] + [0] * (n - 1) for _ in range(m - 1)]
print(f)
for i in range(1, m):
for j in range(1, n):
f[i][j] = f[i - 1][j] + f[i][j - 1]
return f[m - 1][n - 1]
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/unique-paths/solution/bu-tong-lu-jing-by-leetcode-solution-hzjf/
来源:力扣(LeetCode)https://leetcode-cn.com/problems/unique-paths/