计算机图形和动画

一个平面上的图形可以在计算机上存储为一个顶点的集合，通过画出顶点，并将顶点用直线相连即可得到图形(GPU管线中的三角片元和栅格化操作),若有n个顶点，则它们存储在一个 $2\times n$ 的矩阵中，顶点的 $x$ 坐标存储在矩阵的第一行， $y$ 坐标存储在第二行，每一对相继顶点用一条直线相连.

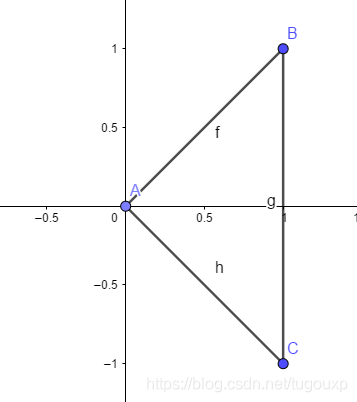
例如，要存储一个顶点坐标位于

$(0,0), (1,1),(1,-1)$

的三角形，将每一项顶点对应的数对存储为矩阵的一列：

$T=\begin{bmatrix} 0 & 1 &1 & 0\\ 0& 1& -1& 0 \end{bmatrix}$

附加顶点 $(0,0)$ 的副本存储在 $T$ 的最后一列，这样，前一个顶点 $(1,-1)$ 可以画回到 $(0,0)$ ,

也就是沿着下图

$\begin{bmatrix} 0\\ 0 \end{bmatrix}\rightarrow \begin{bmatrix} 1\\ 1 \end{bmatrix}\rightarrow \begin{bmatrix} 1\\ -1 \end{bmatrix}\rightarrow \begin{bmatrix} 0\\ 0 \end{bmatrix}$

的轨迹绘制，如下图所示:

通过改变顶点的位置并重新绘制图形，即可变换图形，如果变换是线性的，也就是满足下面两个原则的变换：

原点变换后仍然留在原点
直线变换后仍然是直线

则可通过矩阵乘法来实现,这样的一些列变换就得到一个动画。

比如，第一种

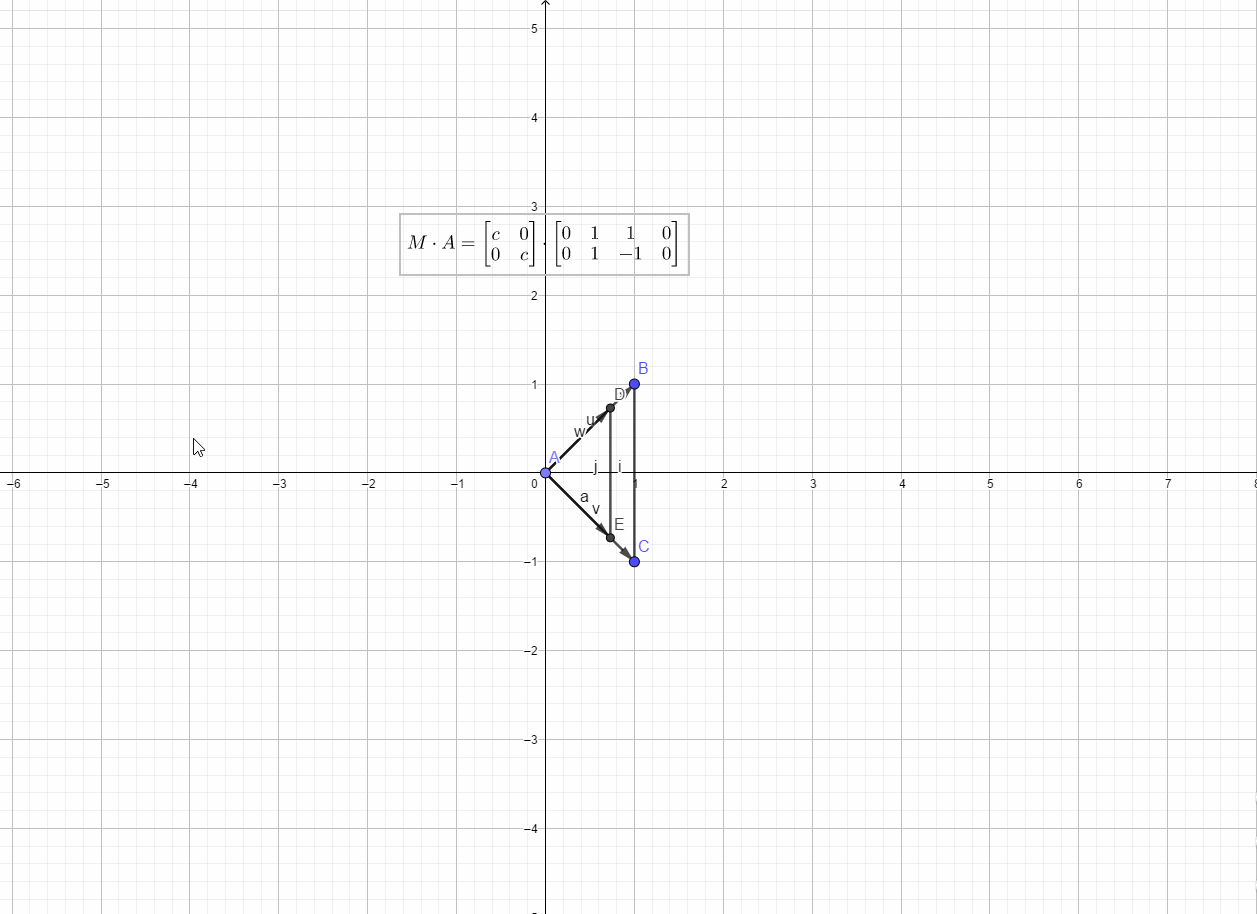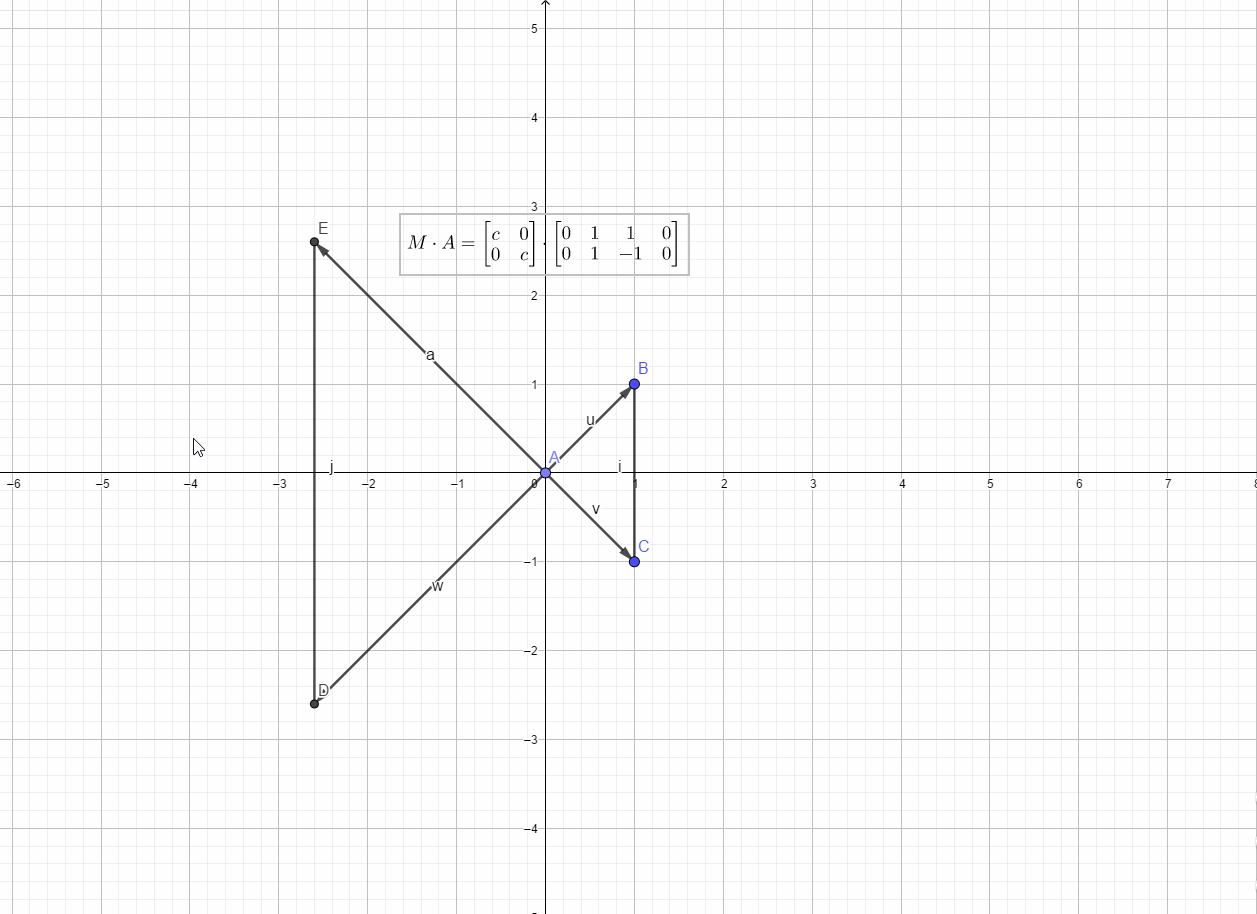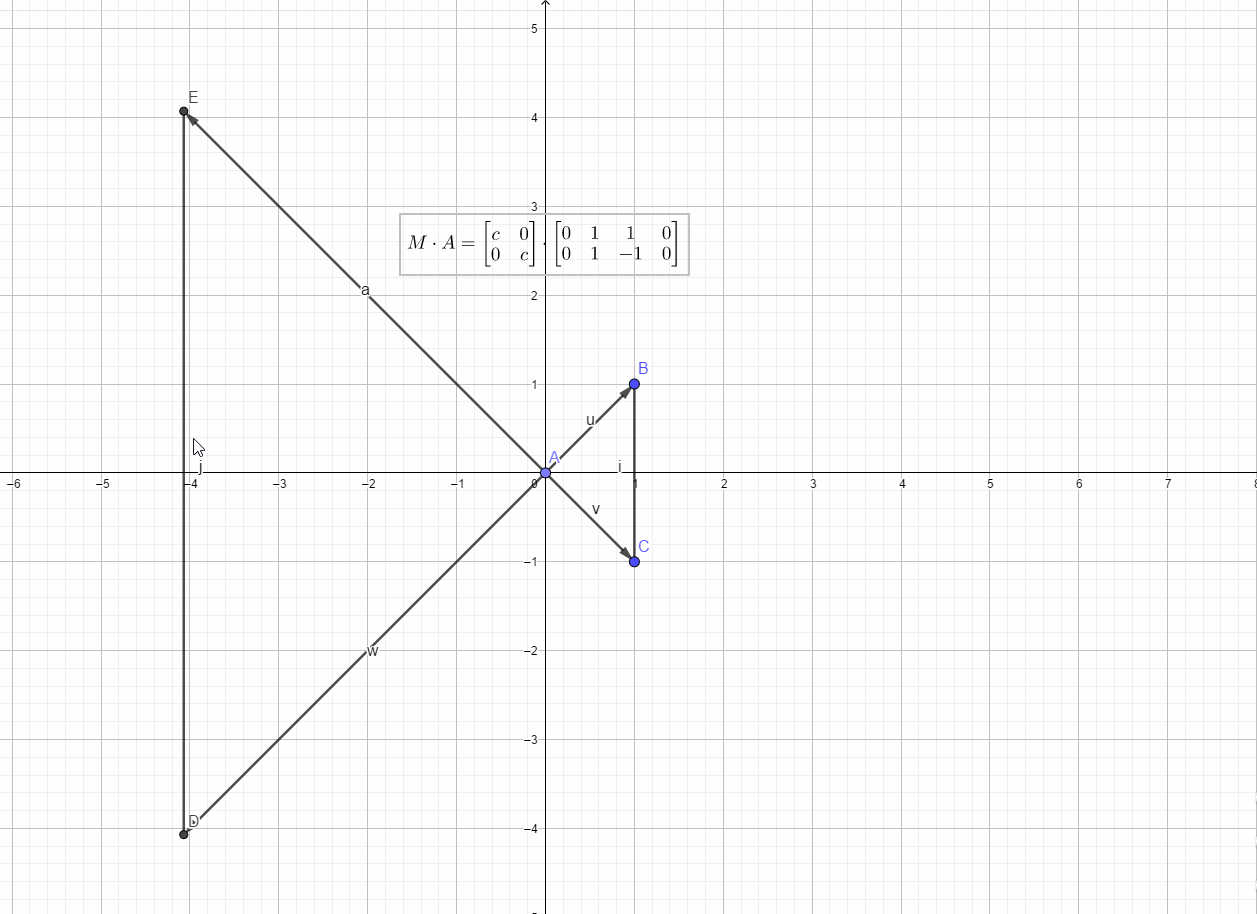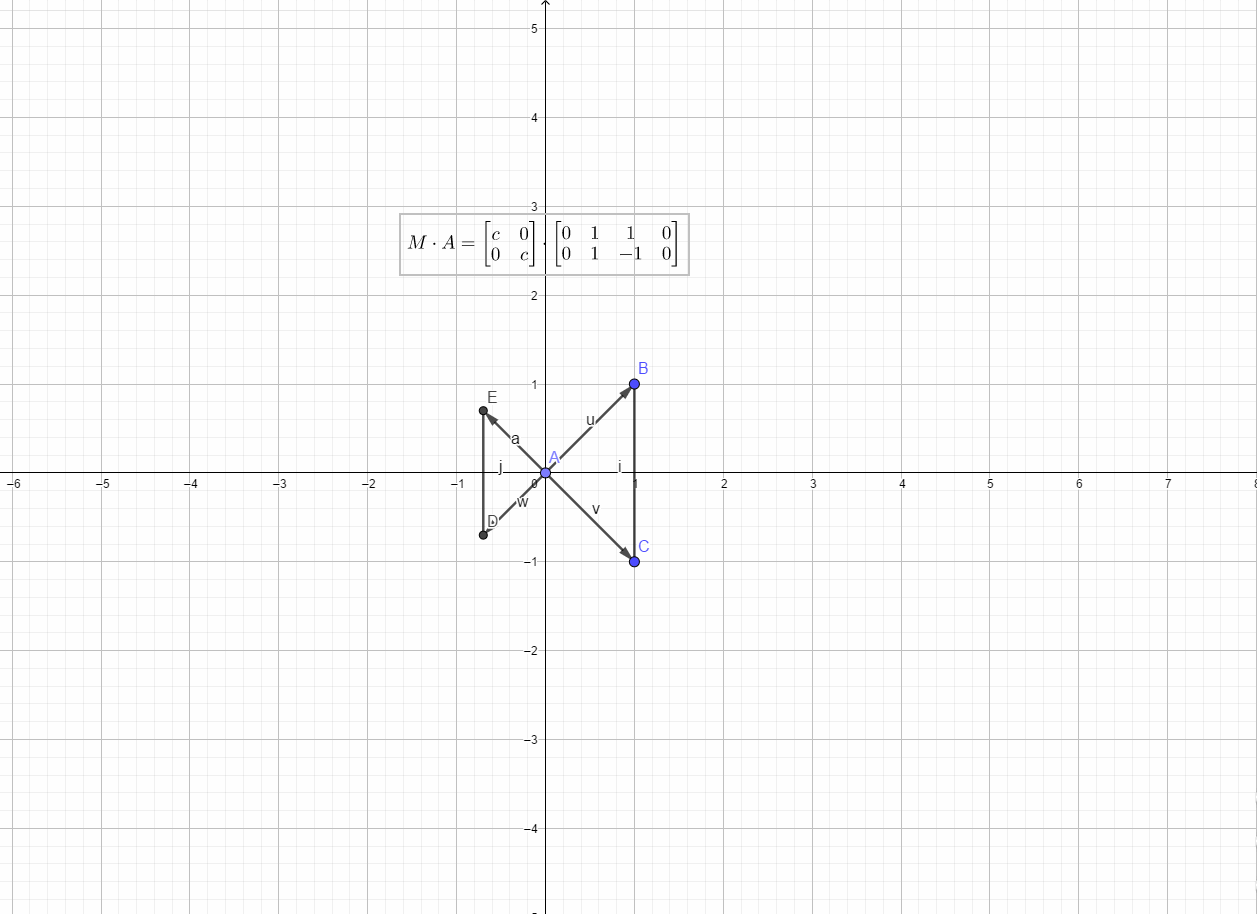
放大和缩小（scaling）

对于形如

$L(\vec{x})=c\vec{x}$

的线性算子，当 $c> 1$ 时为放大，当 $0<c<1$ 时为缩小，算子L可以表示为矩阵

$cE=\begin{bmatrix} c &0 \\ 0 & c \end{bmatrix}$

如下图所示:

第二种

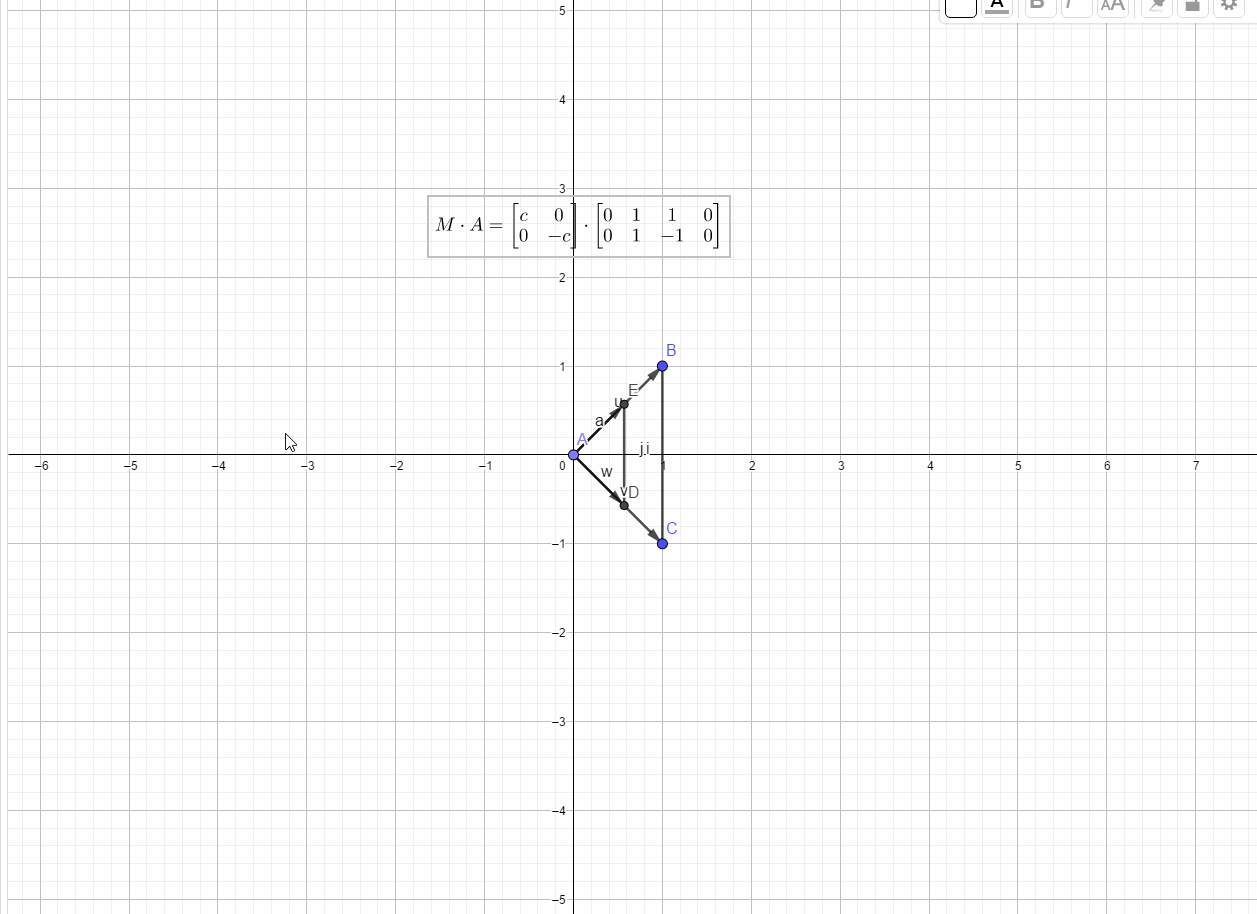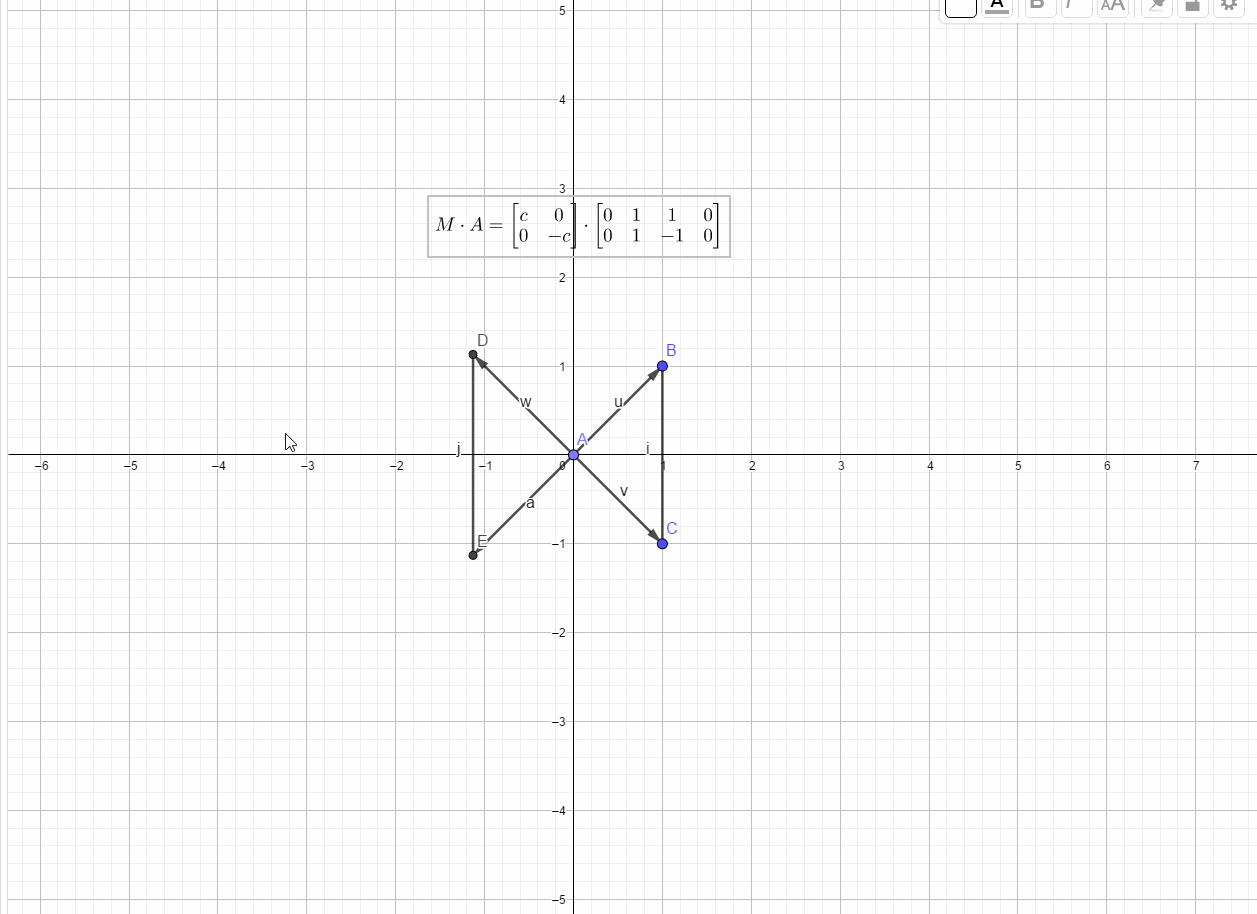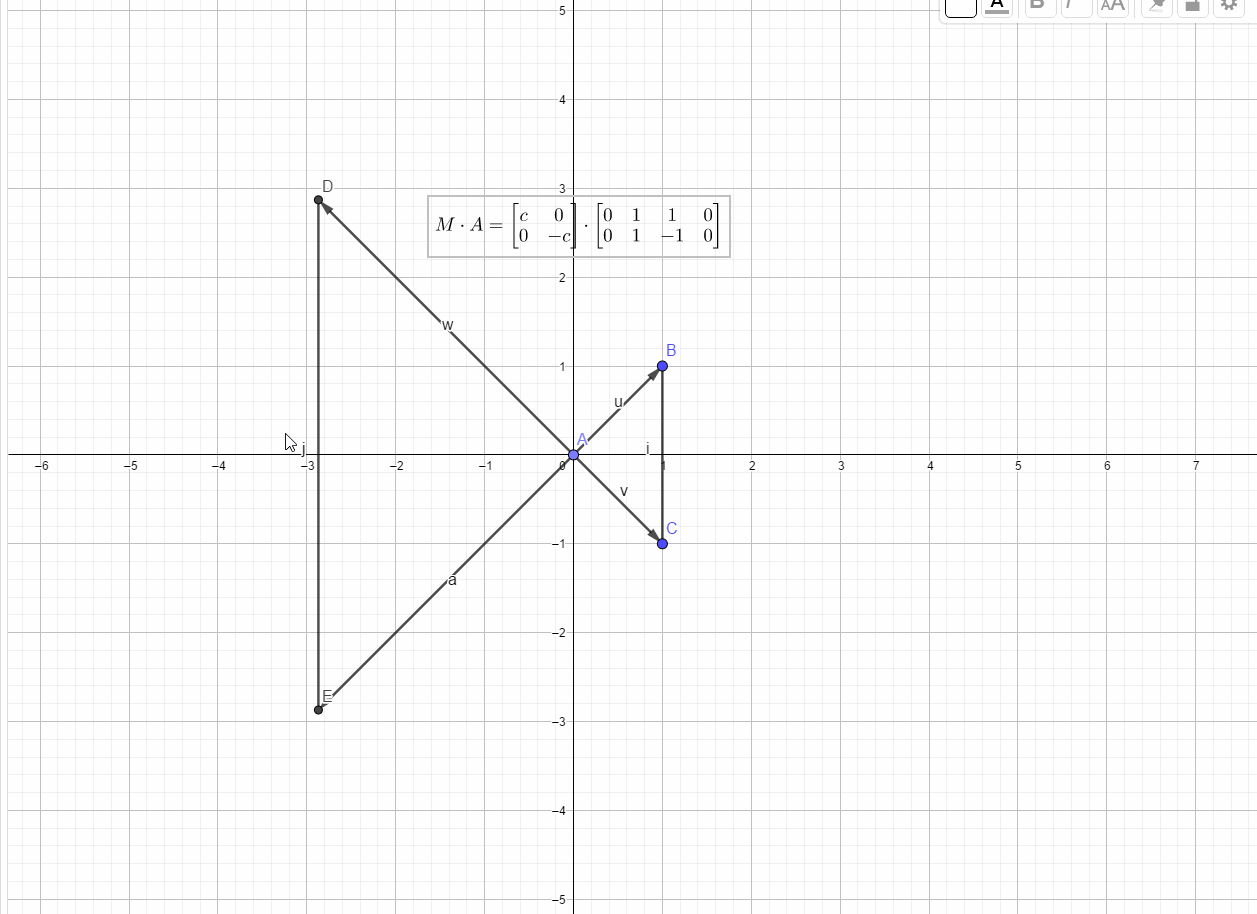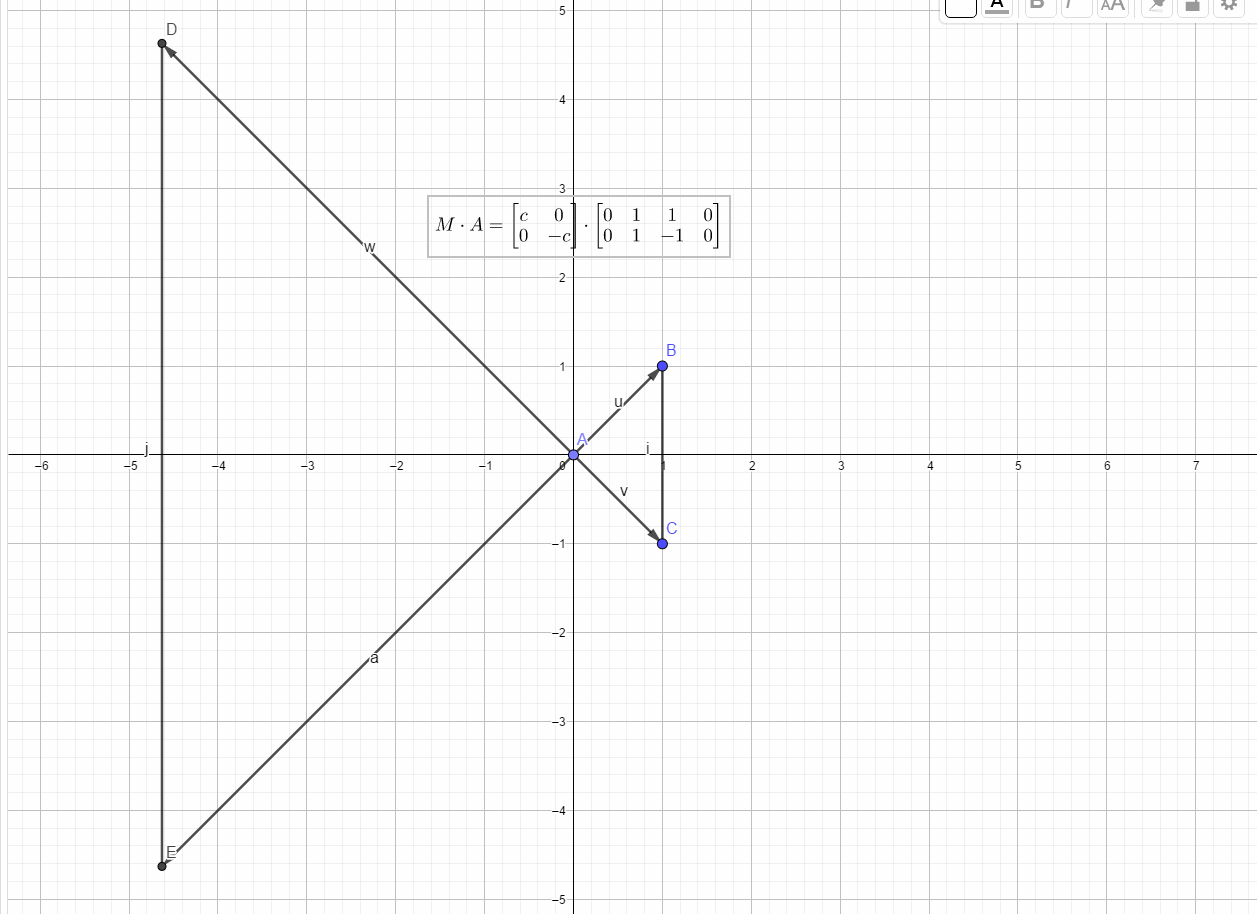
镜像（reflection）

如果 $L_x$ 为将向量 $\vec{x}$ 关于 $x$ 轴对称的变换，则 $L_x$ 满足上述的两条原则，是一个线性变换， $L_x$ 是一个线性算子，且可以表示为 $2\times 2$ 的矩阵A.

因为

$\\L_x(e_1) = e_1 \\ L_x(e_2)=-e_2$

所以

$A=\begin{bmatrix} 1 &0 \\ 0 & -1 \end{bmatrix}$

类似的，关于y轴镜像的变换 $L_y$ 为

$A=\begin{bmatrix} -1 &0 \\ 0 & 1 \end{bmatrix}$

如下图所示:

第三种，旋转

旋转（rotation）

令L为一将向量从初始位置旋转 $\theta$ 角度的变换，也是一个线性变换，满足上面的两条原则。变换矩阵是:

$A=\begin{bmatrix} cos(\theta) & -sin(\theta)\\ sin(\theta) & cos(\theta) \end{bmatrix}$

最后一种，平移

平移（translation)

向量 $\vec{x}$ 的平移变换形如

$L(\vec{x}) = \vec{x} + \vec{\alpha}$

$\vec{\alpha}$ 为一个常向量。

如果 $\vec{\alpha}\neq \vec{0}$ ，则原点会发生移动，所以不是线性变换。且不能表示为 $2\times 2$ 的矩阵。然而，在计算机图形学中，要求所有的变换都能表示为矩阵的乘法，围绕这个问题，引入了一个新的坐标系，成为齐次坐标，这个新的坐标可以将平移表示为线性变换。

齐次坐标系是通过将 $R^2$ 中向量等同于 $R^3$ 中和该向量前两个坐标相同，而第三个坐标为１的向量来构造的．

$\begin{bmatrix} x_1\\ x_2 \end{bmatrix}\rightarrow \begin{bmatrix} x_1\\ x_2\\ 1 \end{bmatrix}$

当需要画出由齐次坐标向量 $(x_1, x_2, 1)^T$ 表示的点时，只要简单的忽略它的第三个坐标并画出有序对 $(x_1,x_2)$ 即可．

前面所讨论的现行变换现在必须表示成 $3\times 3$ 的矩阵，为此，可以将 $2\times 2$ 矩阵通过添加 $3\times 3$ 单位矩阵的第三行和第三列元素进行扩展，例如，将一个 $2\times 2$ 的放大矩阵

$\begin{bmatrix} 3 &0 \\ 0 & 3 \end{bmatrix}$

替换为 $3\times 3$ 的矩阵

$\begin{bmatrix} 3 &0& 0\\ 0& 3 &0 \\ 0& 0 & 1 \end{bmatrix}$

注意到：

$\begin{bmatrix} 3 &0& 0\\ 0& 3 &0 \\ 0& 0 & 1 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ 1 \end{bmatrix}=\begin{bmatrix} 3x_1\\ 3x_2\\ 1 \end{bmatrix}$

若变换将 $R^2$ 中的向量平移向量

$\vec{a}=\begin{bmatrix} 6\\ 2 \end{bmatrix}$

则可以在齐次坐标系中求出变换的矩阵表示，只需要简单的用 $\vec{\alpha}$ 元素替换 $3\times 3$ 矩阵钱两行中的第三列元素即可．也就是

$A\vec{x}=\begin{bmatrix} 1 &0& 6\\ 0& 1 &2 \\ 0& 0 & 1 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ 1 \end{bmatrix} = \begin{bmatrix} x_1 + 6\\ x_2 + 2\\ 1 \end{bmatrix}$

来一副综合效果图，G2D设计中的shear变换，其实就是一个线性空间变换：

结束