【通信原理 入坑之路】—— 【干货】“这里有你想探索的Fourier Transform"：傅里叶变换详细归纳

写在前面：本博文是《深入浅出通信原理》的学习笔记，仅供个人学习记录使用

【 $Blog$ 更新记录：】
最初发表于： $2020-02-06\quad 15:03:25$
第一次更新于： $2020-02-16\quad 10:05:00$ 增加了周期信号和非周期信号连续谱关系的理解

首先，傅里叶变换的本质是求频谱密度！

一、傅里叶变换是如何引出来的

1.1 周期矩形信号的频谱（线谱）

详见这篇blog：【通信原理 入坑之路】—— 周期信号和非周期信号的频谱分析
从上面这篇博客的分析：我们得出：
【1】周期为 $T = T_0$，脉冲宽度为： $\frac{T_0}{2}$时，周期矩形信号的频谱是： $c_k = \frac{1}{2}\frac{T_0}{T}sinc(\frac{k}{2}\frac{T_0}{T}) = \frac{1}{2}sinc(\frac{k}{2})$
【2】周期为 $T = 2T_0$，脉冲宽度为： $\frac{T_0}{2}$时，周期矩形信号的频谱是： $c_k = \frac{1}{2}\frac{T_0}{T}sinc(\frac{k}{2}\frac{T_0}{T}) = \frac{1}{4}sinc(\frac{k}{4})$
【3】周期为 $T = 4T_0$，脉冲宽度为： $\frac{T_0}{2}$时，周期矩形信号的频谱是： $c_k = \frac{1}{2}\frac{T_0}{T}sinc(\frac{k}{2}\frac{T_0}{T}) = \frac{1}{8}sinc(\frac{k}{8})$
注意：我们上面指的是频谱，也就是横坐标是频率，纵坐标是信号在该频率下的复傅里叶系数 $c_k$

在上面的例子中，我们固定了脉冲宽度是 $\frac{T_0}{2}$ ，周期 $T$，因此，我们可以用占空比 $\frac{1}{n}$ 来表示： $\frac{1}{n} = \frac{\frac{T_0}{2}}{T} = \frac{T_0}{2T}$
那么，复傅里叶系数又可以表示成： $c_k = \frac{1}{n}sinc(\frac{k}{n})$
上面3种情况频谱的图片如下图所示：

1.2 非周期信号的频谱（连续谱）

详见这篇blog：【通信原理 入坑之路】—— 周期信号和非周期信号的频谱分析
从上面的分析发现：随着T的增大，线谱中不同频率的谱线的间距越来越小，数量也越来越多，这样不太利于我们对频率的分析，我们引入了连续谱，或者我们叫做频谱密度曲线

这里补充一点上面那篇blog没有提到的一点，我们先来看看概率密度曲线的意义：

红色的曲线就是x的概率密度函数pdf曲线。如果我现在这样问你：P(x = 10) = ?
乍一看，x = 10对应曲线的纵坐标在0.16附近，我们能说x = 10的概率是0.16吗？？

答案是：NO！,P(x=10) = 0!
正如我们在生活中所说的当x=10，我们一般会把10.01，10.001，9.99等等这样的数都当作10，我们以x为某地的降雨量为例，你能保证当天降雨的总量刚刚好在10mm，一滴不多一滴不少吗？

我们上面所讨论的问题，都基于一个前提：就是我们的自变量x是一个连续随机变量，在连续随机变量的概率密度曲线中，x准确等于任何一个数的概率都是0！

那么要怎么表示概率呢？我们可以用一个区间，比如说x在[9.9, 10.1]区间的概率是多少。这样就会取得一个确定的概率P. 在微积分的知识里我们知道，在pdf曲线中计算x落在区间[9.9, 10.1]上的概率就应该是曲线在[9.9, 10.1]那段的面积： $\int_{9.9}^{10.1}f(x)dx$
近似可以看作上图的蓝色矩形的面积。
因此，概率密度曲线中某一x范围 $[x, x+△x]$概率，就是曲线在 $[x, x+△x]$这一范围下与横轴围成的区域的面积

概率密度函数，频谱密度函数，这两者其实内涵是类似的！

概率密度 $P(x)$：对应的是概率，那么曲线在 $[x, x+△x]$这一范围下与横轴围成的区域的面积就是x在 $[x, x+△x]$这一范围下的概率
频谱密度 $X(f)$：对应的是 $c_k$，那么曲线在 $[f, f+△f]$这一范围下与横轴围成的面积就是f在 $[f, f+△f]$这一范围下的 $c_k$

而面积可以近似地以矩形的面积代替，那么矩形的底就是 $△f$，高就是 $\frac{c_k}{△f}$，如下图：

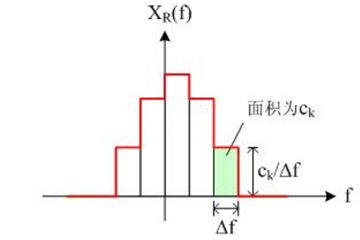
因此，所有的 $\frac{c_k}{△f}$就构成了频谱密度曲线
其中，在上图， $△f$是信号基波的频率 $f$，和信号的周期T有关

1.2.1 由周期信号的连续谱出发

下面我们就来看看频谱密度如何求解：
上面已经知道周期信号的 $c_k$了： $c_k = \frac{1}{2}\frac{T_0}{T}sinc(\frac{k}{2}\frac{T_0}{T}) = \frac{1}{n}sinc(\frac{k}{n}) \tag{1}$
因为我们知道： $△f = f_0 = \frac{1}{T}$，如果现在假设矩形波的脉冲宽度是 $τ$，那么我们得到： $\frac{1}{n} = \frac{τ}{T} = τf_0$
因此上式变为： $\begin{aligned} \frac{c_k}{△f} =\frac{c_k}{f_0} = c_kT&= \frac{T}{n}sinc(\frac{k}{n})\\ &=τf_0Tsinc(τkf_0)\\ &=τsinc(τkf_0)\tag{2} \end{aligned}$

我们结合式子(2)和(3)，我们也能够发现了一个重要关系： $k△f = kf_0 = f$

值得注意的是，在（2）式中， $f_0$ 是周期矩形信号的基波频率，当周期信号的周期 $T$ 趋向于无穷大时， $kf_0$ 就演变为了一般频率 $f$
因此，我们有： $\frac{c_k}{△f} =c_kT = τsinc(τf)$

因此，我们得到：幅度为1，脉冲宽度为： $τ$ 的非周期矩形信号的连续谱是： $X(f) = τsinc(τf)$

--------------------------------------------------------------------------
但是，大家有没有发现周期矩形信号的连续谱和非周期矩形信号的连续谱的关系？
幅度为1，脉冲宽度为： $τ$ 的周期信号连续谱： $X(f) = τsinc(τkf_0)$
幅度为1，脉冲宽度为： $τ$ 的非周期信号连续谱： $X(f) = τsinc(τf)$

我们发现：幅度为1，脉冲宽度为： $τ$ 的周期信号的连续谱是 以采样频率为 $f_0$，对幅度为1，脉冲宽度为： $τ$ 的非周期举行信号连续谱采样得到的结果！

这句话我也是现在才慢慢理解哈哈哈

下面，我们就来看看信号频谱密度的计算： $\begin{aligned} \frac{c_k}{△f} &=c_kT = \int_{-\frac{T}{2}}^{+\frac{T}{2}}x(t)e^{-jkω_0t}dt\\ &=\int_{-\frac{T}{2}}^{+\frac{T}{2}}x(t)e^{-jk2Π△ft}dt\\ &=\int_{-\frac{T}{2}}^{+\frac{T}{2}}x(t)e^{-j2Πft}dt\\ \end{aligned}$
当T=∞时，就有： $X(f) = \int_{-∞}^{+∞}x(t)e^{-j2Πft}dt = \int_{-∞}^{+∞}x(t)e^{-jωt}dt$
这样，我们就推导出了傅里叶变换的计算公式啦！！

二、一些常见信号的傅里叶变换

2.1 周期信号的傅里叶变换

我们来看看周期信号 $x(t)$的傅里叶变换，也就是看看周期信号的频谱密度
因为周期信号都可以化成不同频率分量信号的叠加，用复傅里叶级数来表示就是： $x(t) = \sum_{k=-∞}^{+∞}c_ke^{jkω_0t}$
因此，有：
$\begin{aligned} &\int_{-∞}^{+∞}\sum_{k=-∞}^{+∞}c_ke^{jkω_0t}e^{-jωt}dt\\ &=\sum_{k=-∞}^{+∞}c_k\int_{-∞}^{+∞}e^{jkω_0t}e^{-jωt}dt\\ \end{aligned}$
大家发现了嘛： $\int_{-∞}^{+∞}e^{jkω_0t}e^{-jωt}dt$不就是 $e^{jkω_0t}$的傅里叶变换吗！
我们知道 $e^{jkω_0t}$的频谱，是在 $ω = kω_0$处，幅度 $c_k = 1$的单位冲激函数，傅里叶变化是计算频谱密度，因此，得到： $\lim_{△f \to 0}\frac{c'_k}{△f} = \lim_{△f \to 0}\frac{2Πc'_k}{△ω} = 2Πc'_kδ(ω - kω_0) = 2Πδ(ω - kω_0)$

因此，周期信号的傅里叶变换就等于： $\int_{-∞}^{+∞}\sum_{k=-∞}^{+∞}c_ke^{jkω_0t}e^{-jωt}dt = 2Π\sum_{k=-∞}^{+∞}c_kδ(ω - kω_0)$

2.2 正，余弦信号的傅里叶变换

先来看看余弦信号 $cosω_0t$的傅里叶变换： $\begin{aligned} &\int_{-∞}^{+∞}cosω_0te^{-jωt}dt\\ &=\int_{-∞}^{+∞}\frac{1}{2}(e^{jω_0t} + e^{-jω_0t})e^{jωt}dt\\ &=\frac{1}{2}\int_{-∞}^{+∞}e^{jω_0t}e^{jωt}dt + \frac{1}{2}\int_{-∞}^{+∞}e^{-jω_0t}e^{jωt}dt \end{aligned}$
我们发现这个式子就是分别对 $e^{jω_0t}$和 $e^{-jω_0t}$做傅里叶变换，再乘二分之一。
那么就很简单了，和上面的分析类似，我们有： $\int_{-∞}^{+∞}cosω_0te^{-jωt}dt = Πδ(ω - ω_0) + Πδ(ω + ω_0)$

大家是否觉得 $Πδ(ω - ω_0) + Πδ(ω + ω_0)$这个式子有点眼熟？我们在之前的博客里面分析过：信号 $x(t)$与载波信号 $cosω_0t$相乘，在频域上相当于把 $x(t)$的频谱一分为二，左右各搬移 $ω_0$个单位！ 再结合频域卷积定理，我们就能够再一次推导出这个结论！

频域卷积定理：时域信号 $x(t)$与 $h(t)$相乘，即 $y(t) = x(t)h(t)$，那么： $Y( ω) = \frac{1}{2Π}X( ω)H( ω)$

sin信号的傅里叶变换类似，这里不再赘述

2.3 复指数信号的傅里叶变换

复指数信号，我们这里指型如 $e^{jkω_0t}$这样的信号

$\begin{aligned} \int_{-∞}^{+∞}e^{jkω_0t}e^{-jωt}dt \end{aligned}$
而我们已经知道， $e^{jkω_0t}$的频谱很简单，就是在 $ω = kω_0$位置，幅度 $c_k = 1$的单位冲激函数，即 $δ(ω - kω_0)$，那么，它的频谱密度为： $\lim_{△f \to 0}\frac{c_k}{△f} = \lim_{△f \to 0}\frac{2Πc_k}{△ω} = 2Πc'_kδ(ω - kω_0) = 2Πδ(ω - kω_0)$

2.4 直流信号的傅里叶变换

还记得我们刚刚讲到的复指数信号的傅里叶变换吗？： $2Πδ(ω - kω_0)$，我们只要令 $ω_0$ = 0，即可求出直流信号的傅里叶变换： $2Πδ(ω)$

2.5 单位冲激信号的傅里叶变换

通过我之前几篇blog的记录，大家应该对单位冲激信号不陌生了，它有个特性： $\int_{-∞}^{+∞}δ(t)dt = 1$
下面我们来看看它的傅里叶变换： $\begin{aligned} \mathscr{F}(δ(t)) = \int_{-∞}^{+∞}δ(t)e^{-jωt}dt \end{aligned}$
根据单位冲激函数的性质，只有当t = 0时，δ(t)才不等于0，而此时 $e^{-jωt}$ = 1，因此原式变为： $\mathscr{F}(δ(t)) = \int_{-∞}^{+∞}δ(t)dt = 1$
因此，我们知道：单位冲激信号的傅里叶变换是1， $\mathscr{F}(δ(t))=1$

二、傅里叶变换的对称性

还记得我们在2.4节提到了：直流信号的傅里叶变换是 $\mathscr{F}(1) = 2Πδ(ω)$
我们换一下，以f作为冲激函数的自变量，那么就是 $δ(f)$，即 $\mathscr{F}(1) = δ(f)$
【证明】： $\begin{aligned} \mathscr{F}^{-1}(δ(f)) = \int_{-∞}^{+∞} δ(f)e^{2Πft}df \end{aligned}$
由于单位冲激函数的性质，只有当f = 0时，δ(f)才不为0，而此时 $e^{2Πft}$ = 0,因此： $\mathscr{F}^{-1}(δ(f)) = \int_{-∞}^{+∞} δ(f)e^{2Πft}df = \int_{-∞}^{+∞}δ(f)df = 1$
因此，直流信号1的傅里叶变换是单位冲激函数！， $\mathscr{F}(1) = δ(f)$
而我们刚刚又讨论得出：单位冲激信号的傅里叶变换是1， $\mathscr{F}(δ(t))=1$

这就是傅里叶变换的对称性！

三、傅里叶变换的时移特性

傅里叶变换的时移特性是这样的：若
$\mathscr{F}(F(t)) = F(ω)$
那么： $\mathscr{F}(F(t - t_0)) = F(ω)e^{-jωt_0}$
也就是说如果时域信号 $f(t)$的傅里叶变换得到的频谱是 $X(ω)$，那么 $f(t)$经过时移 $t_0$之后的信号 $f(t - t_0)$的傅里叶变换就等于原来的频谱 $X(ω)$乘上 $e^{-jωt_0}$

我们从定义角度推导一下： $\begin{aligned} \mathscr{F}(f(t-t_0)) &= \int_{-∞}^{+∞}f(t-t_0)e^{-jωt}dt\\ &= e^{-jωt_0}\int_{-∞}^{+∞}f(t-t_0)e^{-jω(t-t_0)}d(t-t_0)\\ &=e^{-jωt_0}\int_{-∞}^{+∞}f(x)e^{-jωx}dx\\ &=X(ω)e^{-jωt_0}\\ &=X(f)e^{-j2Πft_0} \end{aligned}$

简单来讲，信号在时域上的延迟相当于在频域上的旋转，而且，在频率 $f>0$ 时，频域图形顺时针旋转， $f <0$ 时，频域图形逆时针旋转， $|f|$ 越大相当于旋转的速度越快。

四、与傅里叶变换有关的一些重要定理

4.1利用傅里叶变化时移特性证明时域卷积定理

首先介绍时域卷积定理：

若 $y(t)$是由两个时域信号 $x(t)$和 $h(t)$卷积得来，那么有： $Y(ω) = X(ω)H(ω)$

我们来证明一下： $\begin{aligned} \mathscr{F}(y(t)) &= \int_{-∞}^{+∞}[h(t)*x(t)]e^{-jωt}dt\\ &= \int_{-∞}^{+∞} [\int_{-∞}^{+∞}h(τ)x(t-τ)dτ]e^{-jωt}dt\\\\ &= \int_{-∞}^{+∞}h(τ)[\int_{-∞}^{+∞}x(t-τ)e^{-jωt}dt]dτ \end{aligned}$
大家现在看这个式子： $\int_{-∞}^{+∞}x(t-τ)e^{-jωt}dt$是不是觉得非常熟悉了：没错！他就是 $x(t-τ)$的傅里叶变换了，还记得在上一节我们推到的公式吗？ $\mathscr{F}[x(t-τ)] = X(ω)e^{-jωτ}$
将它带入上式，得： $\begin{aligned} &\int_{-∞}^{+∞}h(τ)[\int_{-∞}^{+∞}x(t-τ)e^{-jωt}dt]dτ\\ &=\int_{-∞}^{+∞}h(τ)X(ω)e^{-jωτ}dτ\\ &=X(ω)\int_{-∞}^{+∞}h(τ)e^{-jωτ}dτ\\ &=X(ω)H(ω) \end{aligned}$

先暂时整理到这儿，还有更多关于傅里叶变换的秘密后续持续更新！