原题链接
①. 题目

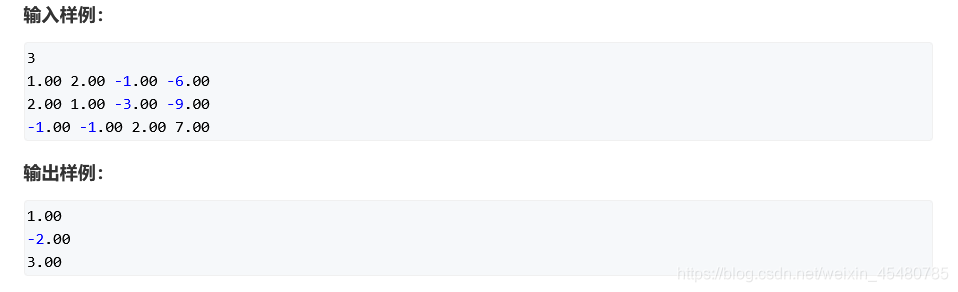
②. 思路
- 这不就是离散数学里的矩阵解线性方程

前置知识:初等行(列)变换
- 把某一行乘一个非0的数 (方程的两边同时乘上一个非0数不改变方程的解)
- 交换某两行 (交换两个方程的位置)
- 把某行的若干倍加到另一行上去 (把一个方程的若干倍加到另一个方程上去)

- 最后再把阶梯型矩阵从下到上回代到第一层即可得到方程的解
算法步骤
- 枚举每一列c,
- 找到当前列绝对值最大的一行
- 用初等行变换(2) 把这一行换到最上面(未确定阶梯型的行,并不是第一行)
- 用初等行变换(1) 将该行的第一个数变成 1
- (其余所有的数字依次跟着变化)用初等行变换(3) 将下面所有行的当且列的值变成 0
③. 学习点
④. 代码实现
import java.util.Scanner;
public class Main {
static int N=110;
static double[][] a=new double[N][N+1];
static int n=0;
static double eps=0.000001;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n=sc.nextInt();
for (int i = 0; i <n; i++) {
for (int j = 0; j <=n; j++) {
a[i][j]=sc.nextDouble();
}
}
int t=guass(a);
if(t==0) {
for (int i = 0; i <n; i++) {
System.out.println(String.format("%.2f", a[i][n]));
}
}else if(t==1) {
System.out.println("Infinite group solutions");
}else {
System.out.println("No solution");
}
}
static int guass(double[][] a) {
int row,col;
for(row=0,col=0;col<n;col++) {
int t=row;
for (int i =row; i <n; i++) {
if(Math.abs(a[i][col])>Math.abs(a[t][col])) {
t=i;
}
}
if(Math.abs(a[t][col])<eps) continue;
for(int i=col;i<=n;i++) {
double temp=a[t][i];
a[t][i]=a[row][i];
a[row][i]=temp;
}
for (int i = n;i>=col; i--) {
a[row][i]/=a[row][col];
}
for(int i=row+1;i<n;i++) {
if(Math.abs(a[i][col])>eps) {
for (int j = n; j >=col; j--) {
a[i][j]-=a[row][j]*a[i][col];
}
}
}
row++;
}
if(row<n) {
for (int i =row; i <n; i++) {
if(Math.abs(a[i][n])>eps) {
return 2;
}
}
return 1;
}
for (int i =n-1; i>=0; i--) {
for (int j =i+1; j <n; j++) {
a[i][n]-=a[j][n]*a[i][j];
}
}
return 0;
}
}