一、关系代数概述

1.1 关系代数运算的特点

基于集合，提供了一系列的关系代数操作：并、差、笛卡尔积（广义积）、选择、投影和更名等基本操作
以及交、连接和关系除等扩展操作，是一种集合思维的操作语言
关系代数操作以一个或多个关系为输入，结果是一个新的关系
用对关系的运算来表达查询，需要指明所用操作，具有一定的过程性
是一种抽象的语言，是学习其他数据库语言，如SQL等的基础

1.2 关系代数运算的基本操作

集合操作
- UNION(并)
- INTERSECTION(交)
- DIFFERENCE(差)
- Cartesian PRODUCT(笛卡尔积)
纯关系操作
- PEOJECT(投影)
- SELECT(选择)
- JOIN(连接)
- DIVISION(除)

二、关系代数之基本操作

2.1 关系代数运算的约束

某些关系代数操作，如并、差、交等，需满足"并相容性"
并相容性
- 参与运算的两个关系及其属性之间有一定的对应性、可比性或意义关联性
- 定义：关系R与关系S存在相容性，当且仅当：
  - 关系R和关系S的属性数目必须相同
  - 对于任意i，关系R的第i个属性的域必须和关系S的第i个属性的域相同

2.2 “并”操作

定义：假设关系R和关系S是并相容的，则关系R与关系S的并运算结果也是一个关系，记作： $R\cup S$ ，它由或者出现在关系R中，或者出现在S中的元组构成
数学描述： $R\cup S= \left \{ t\mid t\in R\vee t\in S \right \}$ ，其中t是元组
并运算是将两个关系的元组合并成一个关系，在合并时去掉重复元组
$R\cup S$ 与 $S\cup R$ 运算的结果是同一个关系

汉语中的“或者...或者...”通常意义是并运算的要求

2.3 “差”操作

定义：假设关系R和关系S是并相容的，则关系R与关系S的差运算结果也是一个关系，记作： $R-S$ ，它由出现在关系R中但不出现在关系S中的元组构成
数学描述： $R-S=\left \{ t\mid t\in R\wedge t\notin S \right \}$ ，其中t是元组
$R-S$ 与 $S-R$ 是不同的

汉语中的“是...但不含...”通常意义是差运算的要求

2.4 “笛卡尔积”操作

定义：关系 $R\left( <a_{1},a_{2},...,a_{n}> \right )$ 与关系 $S(<b_{1},b_{2},...,b_{m}>)$ 的广义笛卡尔积（简称广义积，或笛卡尔积）运算结果也是一个关系，记作： $R\times S$ ，它由关系R中的元组与关系S的元组进行所有可能的拼接（或串接）构成
数学描述： $R\times S= \left \{ <a_{1},a_{2},...,a_{n},b_{1},b_{2},...,b_{m}>\mid <a_{1},a_{2},...,a_{n}>\in R\wedge <b_{1},b_{2},...,b_{n}>\in S \right \}$

$\vee$

当一个检索涉及到多个表时（如果学生表和课程表），便需要将这些表串接或拼接起来，然后才能检索，这时，就要使用广义笛卡尔积运算
$R\times S=S\times R$ ： $R\times S$ 为R中的每一个元组都和S中的所有元组进行串接。 $S\times R$ 为S中的每一个元组都和R中的所有元组进行串接。结果是相同的。
两个关系R和S，它们的属性个数分别为n和m（R是n度关系，S是m度关系）
- 则笛卡尔积 $R\times S$ 的属性个数=n+m
两个关系R和S，它们的元组个数分别为x和y（关系R的基数x，S的基数y）
- 则笛卡尔积 $R\times S$ 的元组个数=x * y

2.5 “选择”操作

定义：给定一个关系R，同时给定一个选择的条件condition(简记con)，选择运算的结果也是一个关系，记作 $\sigma _{con}(R)$ ，它从关系R中选择除满足给定条件condition的元组构成
数学描述：
- 设 $R\left ( A_{1},A_{2},...,A_{n} \right )$ ，t是R的元组，t的分量记为 $t\left [ A_{i} \right ]$ ，或简写为 $A_{i}$
- 条件con由逻辑运算符连接比较表达式组成
- 逻辑运算符： $\wedge ，\vee ，$ ， $\vee$ ，┐或者写为and，or，not
- 比较表达式： $X\theta Y$ ，其中X，Y是t的分量、常量或简单函数， $\theta$ 是比较运算符， $\theta$ 是比较运算符， $\theta \in \left \{ > ,\geq, <, \leq,= ,\neq \right \}$
选择操作从给定的关系中选出满足条件的行
条件的书写很重要，尤其是当不同的运算符在一起时，要注意运算符的优先次序，优先次序自高到低为{括弧； $\theta$ ；┐； $\wedge$ ； $\vee$ }

2.6 “投影”操作

定义：给定一个关系R，投影运算结果也是一个关系，记作 $\Pi_{A} (R)$ ，它从关系R中选出属性包含在A中的列构成
数学描述：
- 设 $R(A_1,A_2,...A_n)$
- $\left \{ A_{i1},A_{i2},...,A_{ik} \right \}\subseteq \left \{ A_{1},A_{2},...,A_{n} \right \}$
- $t\left [ A_{i} \right ]$ 表示元组t中相应于属性 $A_{i}$ 的分量
- 投影运算后可以对原关系的列在投影后重新排列
投影操作从给定关系中选出某些列组成新的关系，而选择操作是从给定关系中选出某些行组成新的关系

三、关系代数之扩展操作

3.1 “交”操作

定义：假设关系R和关系S是并相容的，则关系R与关系S的交运算结果也是一个关系，记作： $R\cap S$ ，它由同时出现在关系R和关系S中的元组构成。
数学描述： $R\cap S=\left \{ t\mid t\in R\wedge t\in S \right \}$ ，t是元组
$R\cap S$ 和 $S\cap R$ 运算的结果是同一个关系
交运算可以通过差运算来实现： $R\cap S=R-(R-S)=S-(S-R)$

交运算操作示例
查询即参加体育队又参加文艺队的学生信息

汉语中的“既...又...”，“...，并且...”通常的意义就是交运算的要求

3.2 “ $\theta$ -连接”操作

投影与选择草醉哦只是对单个关系(表)进行操作，而实际应用中往往涉及多个表之间的操作，这就需要 $\theta$ -连接操作
定义：给定关系R和关系S，R与S的 $\theta$ 连接运算结果也是一个关系，记作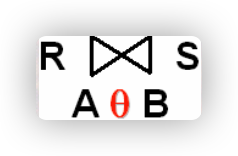，它由关系R和关系S的笛卡尔积中，选取R中属性A与S中属性B之间满足 $\theta$ 条件的元组构成
数学描述：

设 $R\left ( A_{1},A_{2},...,A_{n} \right )$ ， $A\in \left \{ A_{1},A_{2},...,A_n \right \}$
$S\left ( B_1,B_2,...,B_m \right )$ ， $B\in \left \{ B_{1},B_{2},...,B_n \right \}$
t是关系R中的元组，s是关系S中的元组
属性A和属性B是具有可比性
$\theta$ 是比较运算符， $\theta \in \left \{ > ,\geq ,< ,\leq ,=,\neq \right \}$
在实际应用中， $\theta$ -连接操作经常与投影、选择操作一起使用
$\theta$ -连接操作示例

更名操作： $\rho _{sc1}(SC)$ ，将表SC更名为SC1
注意：在理解的时候可以使用笛卡尔积再进行选择来得到 $\theta$ -连接结果，这只是为了方便理解，在DBMS中可以直接进行连接操作，而不必先形成笛卡尔积

3.3 等值连接

定义：给定关系R和关系S，R与S的等值连接运算结果也是一个关系，记作：，它由关系R和关系S的笛卡尔积中选取R中属性与A与S中的属性B上的值相等的元组所组成
数学描述：
当 $\theta$ -丽娜姐中的运算符为"="时，就是等值连接，等值连接是 $\theta$ -连接的一个特例
广义积的元组组合并不是都有意义的，另广义积的元组组合数目也非常庞大，因此采用 $\theta$ -连接/等值连接运算可大幅度降低中间结果的保存量，提高速度
等值连接示例

3.4 自然连接

定义：给定关系R和关系S，R和S的自然连接运算结果也是一个关系，记作： $R\bowtie S$ ，它由关系R和关系S的笛卡尔积中选取相同属性组B上值相等的元组所构成
数学描述：
- 自然连接是一种特殊的等值连接
- 要求关系R和关系S必须有相同的属性组B（如R，S共有一个属性 $B_1$ ，则B是 $B_1$ ，如R，S共有一组属性 $B_1,B_2,...,B_n$ ，则B是这些共有的所有属性
- R，S属性相同，值必须相等才能连接，即： $R.B_1=S.B_1 and R.B_2=S.B_2 ... and R.B_n=S.B_n$ 才能连接
- 要在结果中去掉重复的属性列（因结果中 $R.B_1$ 始终是等于 $S.B_1$ 所以可只保留一列即可）
自然连接操作示例

书写关系代数表达式的基本思路
- 检索是否涉及多个表，如不涉及，则可直接采用并、差、交、选择与投影，只要注意条件书写是否正确即可
- 如果涉及多个表，则检查
  - 能否使用自然连接，将多个表连接起来
  - 如不能，能否使用等值连接或 $\theta$ -连接
  - 还不能，则使用广义笛卡尔积，注意相关条件书写
- 连接完后，可以继续使用选择、投影等运算，即所谓数据库的“选投联”操作

四、关系代数之复杂扩展操作

4.1 “除”操作

除法运算经常用于求解“查询...全部的/所有的...”问题
前提条件：给定关系 $R\left ( A_1,A_2,...,A_n \right )$ 为n度关系，关系 $S\left ( B_1,B_2,...,B_m \right )$ 为m度关系。如果可以进行关系R与关系S除运算，当且仅当：属性集 $\left \{ B_1,B_2,...,B_m \right \}$ 是属性集 $\left \{ A_1,A_2,...,A_n \right \}$ 的真子集，即m<n
定义：关系R和关系S的除运算结果也是一个关系，记作，分两部分来定义
- 先定义 $R\div S$ 结果的属性应该有哪些
- 设属性集 $\left \{ C_1,C_2,...,C_k \right \}=\left \{ A_1,A_2,...,A_n \right \}-\left \{ B_1,B_2,...,B_m \right \}$ ，则有k=n-m则 $R\div S$ 结果关系是k度关系，由 $\left \{ C_1,C_2,...,C_k \right \}$ 属性构成
- 再定义 $R\div S$ 元组怎样形成
- 在设关系和关系，那么关系结果关系为元组的集合，元组满足下述条件：
  - 它与S中的每一个元组 $<b_1,...,b_m>$ 组合形成一个新元组都是R中的某一个元组 $<a_1,...,a_n>$ 。
- 数学描述： $R\div S=\left \{ t\mid t\in \Pi _{R-S}(R)\wedge \forall u\in S(tu\in R) \right\}=\Pi _{R-S}(R)-\Pi _{R-S}((\Pi _{R-S}(R)\times S)-R)$
除操作示例

4.2 “外连接”操作

定义：两个关系R与S进行连接时，如果关系R（或S）中的元组在S（或R）中找不到相匹配的元组，则为了避免该元组信息丢失，从而将改元组与S（或R）中假定存在的全为空值的元组形成连接，放置在结果关系中，这种连接称之为外连接(Outer Join)

外连接=自然连接(或 $\theta$ 连接)+失配的元组(与全空元组形成的连接)
外连接的形式：左外连接、右外连接、全外连接
- 左外连接=自然连接(或 $\theta$ 连接)+左侧表中失配的元组
- 右外连接=自然连接(或 $\theta$ 连接)+右侧表中失配的元组
- 全外连接=自然连接(或 $\theta$ 连接)+两侧表中失配的元组
外连接操作示例

关系模型之关系代数

一、关系代数概述

1.1 关系代数运算的特点

1.2 关系代数运算的基本操作

二、关系代数之基本操作

2.1 关系代数运算的约束

2.2 “并”操作

2.3 “差”操作

2.4 “笛卡尔积”操作

2.5 “选择”操作

2.6 “投影”操作

三、关系代数之扩展操作

3.1 “交”操作

3.2 “ $\theta$ -连接”操作

3.3 等值连接

3.4 自然连接

四、关系代数之复杂扩展操作

4.1 “除”操作

4.2 “外连接”操作

猜你喜欢

关系模型之关系代数

一、关系代数概述

1.1 关系代数运算的特点

1.2 关系代数运算的基本操作

二、关系代数之基本操作

2.1 关系代数运算的约束

2.2 “并”操作

2.3 “差”操作

2.4 “笛卡尔积”操作

2.5 “选择”操作

2.6 “投影”操作

三、关系代数之扩展操作

3.1 “交”操作

3.2 “-连接”操作

3.3 等值连接

3.4 自然连接

四、关系代数之复杂扩展操作

4.1 “除”操作

4.2 “外连接”操作

猜你喜欢

3.2 “ $\theta$ -连接”操作