树形数据结构学习笔记1——线段树与树状数组

在谈树形数据结构之前，先考虑一类问题：

现在要维护一个数列，我需要进行单点或者区间的修改（区间$[l,r]$上都要执行同一个操作），要进行区间的求值，例如求单点或区间和、求单点或区间最大值最小值等等。

这里引出了一个问题，那就是操作的范围，通常有以下两种：单点与区间的修改与求值。而这个直接关系到使用哪一种数据结构的问题，这一问题将在附记3中详解，这里先粗略给一个结论：只存在单点的修改或求值的，可以使用树状数组；既存在区间修改又存在区间求值的，使用线段树

此外，还有另外一个问题关于数据结构的存储方式，将在附记5里详谈，这里给一个结论：树状数组与线段树都是维持了原数列的顺序而未破坏原序。也就是说，它的本质是对线段的维护。

线段树

显然学过数组的都可以直接大模拟的写了：要修改区间，直接用一个循环从$l$遍历到$r$，逐一操作。求和的时候也是逐一操作，多么简单。

可是当这个数列变长到十万这个级别呢？如果一个丧心病狂的人每次都要从最开始加到最末尾，求整个数列的和，进行十万次操作，那这一万亿的操作量受不起啊。所以就要使用一些数据结构来实现这么大量的操作。

（下面是我基于自己的理解写出来的线段树的推导过程）

假设我们真就碰到了这种毒瘤出题人，每次都要从1加到十万，然后再求和，这么搞十万遍，如果知道了真是这种数据，相必大家都想得到一个方法偷懒：我压根就不一个一个改了，直接用一个整数记不就好了，让它代表从1到十万的和，加一次我就直接给它加$10^5\ast add$，然后求和直接输出它就好了，没必要一个一个改一个一个累加了吧。

那如果全是一个固定区间呢？方法不还是一样的，我就只修改这一段的和这一个整数，然后要求和就直接拿这个糊弄一下呗，多省事儿。

可是问题是没有哪个出题人会这么智障的出这种数据，而且我们也无法得知是不是这种数据，那这怎么办呢？

我们就沿用了这种思想：如果要修改一段区间，我只用找到一个或几个整数来代表这一个区间嘛，如果要求和找代表去加就好了。

那估计就有人有疑问了：我每个区间都找一个代表不行吗？

必然是不行的。因为本身就有十万的区间长度，再每个区间找代表，那这不十万乘十万了，空间都炸了。所以我们要合适的选取代表，让每一个区间都能找到一种唯一的代表组合。这个时候我们找到了一种方法：二分。

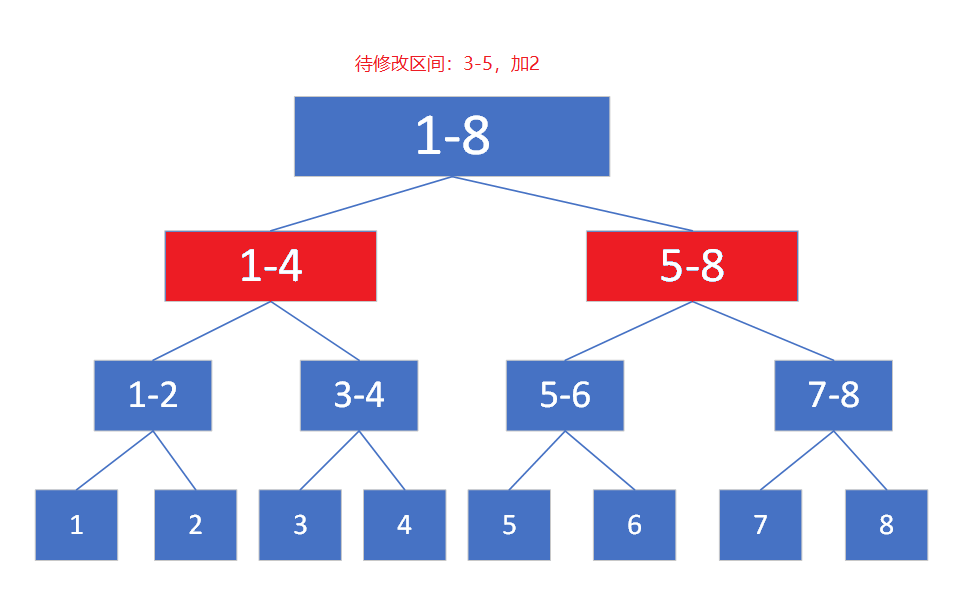
二分，顾名思义，将区间分成等长的两端。例如，对于一个长度为8的数列，我们第一次二分的时候将序列分成$[1,4]$与$[5,8]$，第二次二分将序列分成$[1,2],[3,4],[5,6],[7,8]$，最下层就是每个单元素了。这样，无论来什么区间，我都能唯一表示出来，而且非常方便快捷的找得到。（这也是树状数组的分法，不过有些区别）例如，区间$[3,5]$我就可以分成$[3,4]$与$[5]$，而不会得到另外的一种分法。这种分法可能对人不大友好，但对电脑非常友好：一个递归即可（下文会讲如何实现）。

这样，对于每一次修改，我们都可以找代表去修改，求和也找代表去求和，而不用每次都找到每个数去求和和改。

但是有人肯定会发现一个问题：可是你找代表修改完之后，下面的值并没有改，如果求和的时候不是找代表而是找的代表下面的代表，怎么办？这就是懒标记的作用了，下文也会详细讲述。但是在讲这一个之前先讲基础操作。

所以这就是线段树了：树上每一个节点都代表一个线段的一些信息。

要用线段树，就要先建树。

void build(int place,int left,int right)
{
    
    
    if(left==right)
    {
    
    
        sum[place]=a[left];
        return;
    }
    int mid=(left+right)>>1;
    build(place<<1,left,mid);
    build(place<<1|1,mid+1,right);
    sum[place]=sum[place<<1]+sum[place<<1|1];
}

树作为一种递归结构，线段树的建立也是通过递归实现的。left与right在此约定：覆盖区间的左右范围。当left与right相等时，已经到了叶子节点，递归终止，此时的sum值就等于当前节点left的值，同时返回。然后进行左右子树的递归建立过程。左右子树建立完成后，需要用左右儿子的值来更新当前节点的sum值：左右相加。如果是最大最小值，那么就是左右儿子中较大或者较小的值。

然后说明一下左右儿子的编号问题：一个是$2i$(即上文的place<<1),一个是$2i+1$(即上文的place<<1|1)。

首先先放一颗满线段树来看看：

所谓满线段树，即是数列长度刚好是$2^n$的时候，例如8，如上图，没有哪个非叶子节点是只有一个或者没有儿子的。标号很明显就可以看出来是满足这个规律的。按照上文所述的建树方法编号就是这种排布方法。

但是这种情况必然只是少数，大多数情况下不是这个形式，怎么办？

一种解决方法是填到$2^n$去，强行凑成满二叉树。例如，9->16，27->32。这确实是解决了树不满的情况，但是这也太浪费空间了。线段树是要开4倍空间的，如果再浪费这么多空间，那真是说不过去了。所以我们可以就让它不满着，然后来看看这种情况下的子节点编号问题。

发现没，还是满足的诶！

这图和上图有啥不同的，无外乎就是最小面的一层右下边没有了嘛，上面又没有影响，那顺着编号的怎么会有错呢？所以没必要这么凑，直接大胆建树就好了。

线段树的本质就是二分，这也是它的核心优点。对于每次处理，如果待修改区间已经被完全包含(start<=left && right<=end)，那么这个区间被包含了，直接在祖先节点标记，也是一个递归地终止条件。如果不是，只需要不断地对当前区间二分，如果左区间涉及修改，那么就在左区间去重复这个操作，右区间有要修改部分就到右区间去重复。**注意，这里是只要左右区间有待修改部分就要进去修改，而不是完全包含关系。**整个的模拟过程见下图。

例如，我们现在要对区间$[3,5]$整体加上$2$

首先，我们先从整个开始：$[1,8]$

对于$[1,4]$，涉及区间$[3,4]$，因此指下放到右侧区间$[3,4]$。对于右侧区间，$5$在$[5,6]$中，两侧都要下放!

在$[3,4]$中，两侧都要下放。在$[5,6]$中，只包含5这个单元素，只下放到左侧区间。

5已经完全包含在$[3,5]$中，因此过程结束。

修改代码实现如下：

void change(int place,int left,int right,int start,int end,long long x)
{
    
    
    if(left==right)//必须放到最下层去，否则就会出现代表修改了而下层未修改的情况。要想不完全放下去请参看下文的懒标记。
    {
    
    
        sum[place]+=x*(right-left+1);
        return;
    }
    int mid=(left+right)>>1;
    if(start<=mid)
        change(place<<1,left,mid,start,end,x);
    if(end>mid)
        change(place<<1|1,mid+1,right,start,end,x);
    sum[place]=sum[place<<1]+sum[place<<1|1];//注意这里：因此下层修改完成之后上面的值也应该跟着修改。
}

求和过程类似，只要左侧区间存在待求和区间，就要进去算。整体代码与change非常类似。

long long query(int place,int left,int right,int start,int end)
{
    
    
    if(start<=left && right<=end)//这里就不用下放了，因为代表的值都是正确的，已经可以代表整条线段了。
        return sum[place];
    int mid=(left+right)>>1;
    long long ans=0;
    if(start<=mid)
        ans+=query(place<<1,left,mid,start,end);
    if(end>mid)
        ans+=query(place<<1|1,mid+1,right,start,end);
    return ans;
}

但是这个地方我们却不用涉及到每个叶子节点，因为有些父节点已经帮我们算好了这个区间和，因此不必下放。

在我们上面的讲述中，我们提到了线段树的优越性：二分。每次处理都一层一层的放下去，最后只用涉及log层。可是，如果真就这么模拟而没有任何优化的话，那显然还不如普通的数组。因为普通的数组只用从前到后的遍历，而不需要访问它们的父节点以及祖先节点。而线段树每次都要直接放到最下面，反而增加了操作的数量：从n变成了2n（最劣情况）。这种线段树的时间复杂度是$O(n^{2}logn)$，甚至劣于普通数组。所以我们要想办法优化它。

其中很重要的优化就是懒标记lazytag（下文统称tag）。顾名思义，懒标记，就是因为如果整个区间都需要做这个操作，我就让祖先节点记录这个事情，而不直接对叶节点进行操作。这样覆盖区间越大，反而操作越少——因为可以悬在更高的层面而不用放下去。这样可以大大节约时间，这样才是我们通常意义的线段树，时间复杂度为$O(nlogn)$，这才优于普通数组。

那么tag是如何实现的呢？

先从单标记开始。所谓单标记，就是只有一种操作，如线段树1，只有一个加操作。如果存在多个操作，那么就需要多个tag进行标记。显然，对于每一个操作都需要一个tag，有几个操作就有几个tag。

此处拿线段树1举例。我们可以注意到上面线段树的操作，到了$[3,4]$的时候我们还要往下放，这其实有些不合理，因此已经完全包含，我们没必要将其下放到每一个节点，只要标记祖先就可以了。所以带tag的线段树就少了两步下放，最后只有5这一个下放。

这就减少了许多操作。

但是这也存在了一些问题：等到我们要求和的时候，如果我们要求完全包含$[3,4]$，那还好说；如果要求$[4,7]$，或者$[1,3]$，那我们就要访问到单独的3或者4了，那这没有直接放到最底层怎么办？我们这个时候就需要pushdown操作。

pushdown，顾名思义，下放操作。它的目的是将标记在祖先节点的tag下放到子节点，这个时候再来真正向下改变。因此它叫懒标记也不无道理——只有要检查了才改，要不然就让它悬在上边吧。

void f(int place,int left,int right,long long x)
{
    
    
    sum[place]+=x*(right-left+1);
    tag[place]+=x;
}
void pushdown(int place,int left,int right)
{
    
    
    int mid=(left+right)>>1;
    f(place<<1,left,mid,tag[place]);
    f(place<<1|1,mid+1,right,tag[place]);
    tag[place]=0;
}

注意这个最后的tag归零的操作。已经下放证明当前已经是完全放完的结果，答案正确了就不应该再保留懒标记了，因为已经勤快过了。

对于只有单个的操作，pushdown操作比较简单，就是子节点的tag也要跟着改，和也要改。这个地方要说明一点：tag只的是子节点的状态，当前节点的状态已经被修改完成。所以子节点的和也要进行修改。

这个pushdown调用频率其实是很高的：change的时候要下放，求和的时候更要下放。一旦涉及到区间分裂，就要pushdown：因为毕竟对于左右子区间不是都要进行修改的。

单个操作的说完了，就来了多操作，这也是重头戏。当有多个操作的时候，根据上文的逻辑，我们需要多个tag进行维护。那么与此同时，pushdown的操作也变得复杂了起来。

以线段树2举例：我又要加又要乘。那么怎么办？一条：注意tag的顺序问题

还是区间$[3,5]$，我要先加5，再区间乘以3，最后再加4。如果列成算式，那么就是$3\ast 4+5$。

那么在tag上应该怎么体现呢？如果我两个tag完全不相关，那么在最后一步操作结束后，加法的tag变成8，乘法的tag变成4，最后结果怎么算都是错的，原因就在于3没有乘上4就和5结合了，原式变成了(3+5)*4。那这肯定是不能接受的。

所以我们要求：tag之间必须满足顺序关系。例如，在这个例子中，就必须要求乘法在加法前，就是两个tag最后表示出来的关系应该总满足$a\ast b+c$的关系，其中a是原来的加法tag，b是乘法tag，c是父节点下放下来的tag，无论来了谁都要这样。如果不满足我们就要通过调整使得它满足这个形式。

例如，我现在就要执行上文提到的这个过程。起先两个tag的组合关系是$0\ast 1+0$。我来了一个3，没问题，直接在后面补上3，变成$0\ast 1+3$。这个时候来了4，要在外边包起来一个乘法了，这可不行，那么我就让整个里边变成新的a，也就是让$0\ast 1+3$变成3，再让它去乘4，变成$3\ast 4+0$。后面再来一个5，补在后面就好。这样计算就是正确的。

那么提炼出来整个的过程：乘法tag直接乘上父节点的乘法tag，对于加法tag，就要先乘以父节点的乘法tag（最后这个变成自己的乘法tag了），以变成新的a，再补上外层的父节点加法tag，使得加法总在乘法后。

以下是实现代码：

void pushdown(int place,int left,int right)
{
    
    
    int mid = (left + right) >> 1;
    t[place << 1].sum = (t[place << 1].sum * t[place].mul_tag % mod + t[place].add_tag * (mid - left + 1) % mod) % mod;
    t[place << 1].mul_tag = (t[place << 1].mul_tag * t[place].mul_tag) % mod;
    t[place << 1].add_tag = (t[place << 1].add_tag * t[place].mul_tag + t[place].add_tag) % mod;
    t[place << 1 | 1].sum = (t[place << 1 | 1].sum * t[place].mul_tag % mod + t[place].add_tag * (right - mid) % mod) % mod;
    t[place << 1 | 1].mul_tag = (t[place << 1 | 1].mul_tag * t[place].mul_tag) % mod;
    t[place << 1 | 1].add_tag = (t[place << 1 | 1].add_tag * t[place].mul_tag + t[place].add_tag) % mod;
    t[place].mul_tag = 1;
    t[place].add_tag = 0;
    return;
}

最后一样也是要归零。注意乘法tag应该是归一。

如果有更多的操作呢？我们就需要去发掘一个tag的标记顺序。大致的顺序是：乘法+加法+强制更新（直接将区间值赋为一个值）。对于今年CSP的第五题涉及到的“动力转向”，将$x,y,z$更换成$y，x，z$，这个操作在最内层。总之这个顺序的存在保证了即使未下放值也是正确的。

当然还有一种标记始终不下放的写法，这直接回避了这类问题：所有的修改全部挂靠在懒标记上而不对任何值进行修改，每次求和的时候需要将值与tag值相加得到。这种写法暂时不会，因此不详写。

下面来讲一个比线段树稍微简单一点的树形数据结构：树状数组。而且树状数组的节点也比线段树少。

树状数组

先上图：

和线段树一样，树状数组的思路也是二分。我们同样可以随意指定一个区间，得到它的唯一区间分解方式。例如$[3,5]$，我们还是可以拆成$[3,4]$和$[5]$

但是树状数组构造方式有些奇特。来对比一下线段树和树状数组

这是线段树。

这是树状数组。是不是感觉比线段树少了一些节点？这也是它省空间的地方。

接下来来观察一下它的求和规律。最下层是原数列，而在上面的节点为求和节点。

整理一下：

$sum[1]=a[1]$

$sum[2]=a[1]+a[2]$

$sum[3]=a[3]$

$sum[4]=a[1]+a[2]+a[3]+a[4]$

$sum[5]=a[5]$

$sum[6]=a[5]+a[6]$

$sum[7]=a[7]$

$sum[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]$

依次类推。

有没有点什么规律？这里要请出lowbit函数了。

先来谈谈什么是lowbit函数：

int lowbit(int x)
{
    
    
    return x&(-x);
}

就这一行，看起来非常的简单。我们来分析一下它的工作原理：

在计算机中，负数是用补码储存的。按照现在的计算机，一个short为16位二进制位的话，$-1=(1111111111111111{)}_2$，$-32768=(1000000000000000{)}_2$，也就是说，在负数这边，依旧是谁大的话，谁去掉符号位谁依旧大，可以认为是负数的这些数在负数区重新编号，最小的-32768编号为0，而-1最大编号为32768。补码与原码（每一个绝对值相等的正数与负数区别只有符号位不同而已）的关系是按位取反再加1，互相转换都是这个规则。

那么，对于x&(-x)，计算机干了啥呢？拿5举例。5的补码是$(11111111111111111111111111111011{)}_2$，与上5$(101{)}_2$，得$1$。

试着算算1-8的lowbit？

$1:1$

$2:2$

$3:1$

$4:4$

$5:1$

$6:2$

$7:1$

$8:8$

发现规律没？最后的一个1的位对应的二进制数吧。所以这就是为什么叫lowbit：最后一个1的bit的位置。

基于这个原理，我们来进行树状数组的操作了。

首先是建树。但是这个建树本质没有操作：只有修改求和才会用到各级sum节点，因此省去。

然后是单点修改。注意：这里只能是单点修改，对于区间修改可以使用树状数组：我们使用前缀数组。但是在树上的操作只能是单点修改。

void update(int i,int k)//i为待修改的值的位置，k为待加的值。
{
    
    
    while(i <= n)
    {
    
    
        sum[i] += k;
        i += lowbit(i);
    }
}

结合图来看：

首先我们发现所有的求和节点编号都是按照当前求和区间最大值来决定的。由于二进制的工作原理，不可能存在一个数同时是两个区间的末尾。

看完代码之后我们发现是一层一层往上走的。拿修改第五个数举例：i=5，然后在5这一级sum节点要加5（只有一个值要改所以直接加就好了），然后往上走。一次lowbit之后走到了6（lowbit(5)=1），按照图刚好是sum[5]的上级节点sum[6]，加上5这次加的值，继续往上走：走到看8(lowbit(6)=2)，再加5，就出去了（到了16），循环终止。

结合lowbit函数的特点我们来分析一下：lowbit函数指出了最后一个有1的位置，每一次加上这个值之后，必然最后一位的1和lowbit函数的1相加进位，这一位的1变成了0，节点层数增加（层数越低最后一位的1越小）。经过若干次操作之后，在范围内的1全部被进位掉了，因而停止。

例如：一个长度为64的数列，要修改第47项，路径如下：

47(47)->48(47-48)->64(1-64)。显然只有这几项是包含47的，因此只用修改三项即可。

修改是一个向上的过程，而求和则相反：是向下的过程。

int query(int i)
{
    
    
    int res = 0;
    while(i > 0)
    {
    
    
        res += sum[i];
        i -= lowbit(i);
    }
    return res;
}

注意：这个函数值能求出数列$a[1]-a[i]$的和。如果要求区间$[l,r]$，请两次调用这个函数，$query(r)-query(l-1)$。由于编号特性，这个i代表了当前求和的最后一位。先加上它覆盖的这一段，然后往前走。例如，我要求1-6的和，那么我先访问到了sum[6]，求出了5-6的和，然后一次lowbit去掉了最低位（被lowbit函数减掉了），刚好暴露出[1,4]的和的位置sum[4]，加上它之后就没有1了，循环终止。所以它的移动顺序是：往上走，走到上一层的前祖先节点。此处并没有按边去走。

如果还没有了解，举个例子：对于一个长度为64的数列，求1-47的和。

路径如下：47(47)->46(45-46)->44(41-44)->40(33-40)->32(1-32)

（由于对树状数组不熟悉，因此不再详细讲述了）

总之，线段树和树状数组这两个以二分为基础的数据结构用途广泛，因此在此详细介绍。