树形数据结构学习笔记2——堆与二叉堆

本文作为堆的基础，只涉及最基础的二叉堆。同时为了行文方便，约定本文中的堆都是大根堆。

什么是堆？就是将尽可能大的元素往上放的一种数据结构。（注意与下一篇：二叉搜索树（BST）区分开）

这是二叉堆。

而这是下篇文章要讲的BST。

（它们俩差别还是挺大的）。

而二叉堆，就是每个父节点下面至多有两个子节点的一种堆。

细心的应该有人发现了：堆的左右儿子好像没有明显大小关系。左儿子可以大于右儿子，也可以小于。而且左子树内的元素大小也和另一个子树完全没有关系。也就是说，二叉堆中只有根节点最大这么一条限制，下面的想怎么玩儿就怎么玩儿。

而这个也带来了一些不便——显然只有访问最大值是比较方便的。STL当中的优先队列，就是二叉堆。

接下来来讲一下二叉堆是如何使用的。

以下的二叉堆都是以数组作为载体，和线段树一样。由于二叉堆的这种二分结构，因此它访问子节点和父节点的方式和线段树一样：

左儿子：place<<1

右儿子：place<<1|1

父节点：place>>1

建堆（维护堆的性质）

和线段树一样，都是要从最底层开始摆放元素，但是它没有额外空间。注意到我们在线段树的附记5探讨过数据存储方式，线段树保留了原来的输入顺序，而二叉堆则没有——输入顺序将在建堆过程中被打乱。

与其说它在建堆，不如说它只是在调整数列中数的顺序，让它符合堆的要求。

首先来看它的操作过程。约定：数组长度为n，堆的大小也为n。

先来看一个最基础的操作——max_heaplify（维护堆性质）

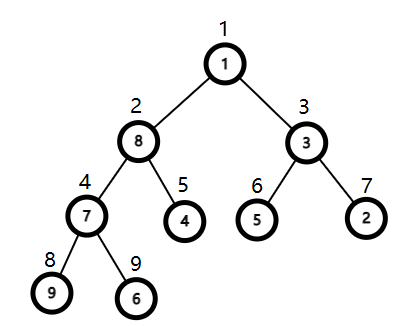
现在有一个乱序的数组：$1,8,3,7,4,5,2,9,6$。为了观察便利，画成一个二叉堆的形式。

显然它不符合二叉堆的性质，因而需要调整。我们先从最简单的结构看起：

红色标出的结构中，如果这里都不满足那不用看了。那我们应该怎么做呢？

显然两个儿子都比根大，这是不合规矩的。由于根是根、左右儿子这三者中最大的元素，我们只需要找到左右儿子中大的，往上放就可以了。

标红的结构就已经搞好了。显然二叉堆就是由大量的这样的小结构构成的，对于每一个这样的小结构都可以使用这种方法处理，然后整合起来，就可以了。

但是可以注意到，我们上来先搞堆顶，使得下面不一定满足，因此真正建堆的时候是从下往上处理的。

因此在建堆的时候，首先是要先维护堆的性质（max_heaplify）。这一过程通常像线段树一样递归操作。

void max_heapify(int place)
{
    
    
	int left=place<<1;
	int right=place<<1|1;
	int index=place;//左右儿子和根节点中最大值对应下标
   //这里经过他人点拨，需要判断有没有左右儿子，这样可以简化其他操作。
	if(left<=n && a[left]>a[index])//左儿子比最大值大，更新
    		index=left;
	if(right<=n && a[right]>a[index])//右儿子同理
    		index=right;
	if(index!=o)//最大值不在根，那么就把最大值换到根上来，把原来根的元素放下去
   	{
    
    
		swap(a[place],a[index]);
		max_heapify(index);//由于交换，那个儿子对应的大根堆性质不一定保持，因此需要递归的处理
	}
}

由主方法可以知道，它的单步复杂度仅为logn。

当然它也有迭代写法，这里不再赘述。

然后，就要建堆。这一过程仰赖维护堆性质这一过程，代码非常简单：

for(int i=n/2;i>=1;i--)//从后往前的进行，这样就不会造成二次修改
	max_heaplify(i);

这样就可以建起一个大根堆了，按照次序访问这个堆，就可以给数组排序。这就是堆排序，时间复杂度nlogn。

插入元素

由于我们是数组，显然不便于插入到数组的中间。因此每次操作的时候插入到数组尾端就行。

但是这样又可能破坏了大根堆的性质，因而需要调整函数（shiftup）。首先来看看它的操作过程。

这是现有的一颗二叉树。节点上方编号为数组下标。

现在我们要插入元素15，放入下标为13的地方。

显然这样做之后6、12、13这个小大根堆的性质被破坏了，进行调整：把子节点中大的换上来，根换下去。

然后3、6、7这个大根堆又坏了……继续调整。

现在1、2、3这三者关系总算是符合了，可以停止了。

因此总结一下：从最后面插入，依次上浮，直到无法调整或者已经到顶。显然每一层只用操作一次，复杂度logn

上代码：

void shiftup(int place)
{
    
    
	int father=place>>1;
	if(father>=1 && a[father]<a[place])//存在父节点，并且与父节点相冲突（破坏大根堆性质）
   	{
    
    
		swap(a[father],a[place]);
		shiftup(father);
	}
}

由主定理可以知道时间复杂度仅为logn——每层就操作了一个数。

弹出元素

这里的弹出元素，通常是指弹出最大值，也就是堆顶。显然我们很容易访问到最大值——毕竟就在数组的第一个元素。但是如果要弹出怎么办呢？

我们拿上一个插入好了的二叉堆举例。

我们现在要弹出16了。

但是一个堆不能没有根啊。于是我们就找叶节点来顶。因为这样就不存在子节点又没有父亲的情况。于是我们把最后一个元素顶上来。

那现在这个不就变成了维护堆的性质吗？heaplify走起。

所以我们的过程就是——把最后一个元素放上来，然后从上到下进行一次更新（heaplify）。总复杂度logn。这样做也是尽可能不破坏二叉堆的结构，让树保持相对平衡的状态，而不会退化成链增加复杂度。

void pop()
{
    
    
	a[n--]=a[1];
   	max_heaplify(1);
}