树形数据结构学习笔记3——BST（二叉查找树）

在上文中我们提到了一种和二叉堆长的很像的数据结构——BST。本文就来讲述这种数据结构。

先看图：

这很明显还是一棵树。每个节点至多两个儿子，节点维护一些信息。

和二叉堆不同的是，BST中父节点和子节点的关系是左儿子<父节点<右节点，而且更一般的，右子树中元素都大于根，左子树中元素都小于根。而这正是它可以进行搜索的依据。

注意：我这里没有提及相等元素的情况。对于相等形况，通常是挂靠在同一节点，在节点中新增一个信息：该元素出现的次数。因而下文不再涉及相等情况，如若相等直接停止，元素出现次数+1。

查找

回忆二叉堆，我们只能够访问最大值，其他的值由于不知道摆放位置而无法访问。但是这种摆布方法就可以让每个节点变得可以访问了：如果待查元素比枢轴元素（根节点）大，就去右子树查；如果小于，那么就在左子树查。

基本的访问规则：从根开始，如果大于，就去右子树，反之就去左子树，如果相等就找到了，递归的进行上述过程，直到叶节点结束。

例如，我们要在上面这颗BST中找到4。

我们从根节点7开始，发现4<7，则去左子树查找。

对于左子树的根5，4<5，继续去左子树查找。

3>4，因而去右子树，最终在叶子节点找到了4。

这么能成功的原因在于：如果去了左子树，右子树中一定不存在：都已经比根节点小了，右子树都比根节点大，那不是白搞？所以我们可以像二分查找那样丢掉一半的解空间，实现对数级别复杂度。而二叉堆就不行：左右子树都可能有这个数，因而不能随意丢弃解空间。

代码如下：

int search(int place,int x)//x为待查元素，place为当前枢轴元素，返回x的下标。-1为未找到
{
    
    
	if(t[place].value==x)//当前节点值等于x
		return place;
	if(t[place].value<x)//x大于枢轴元素
	{
    
    
		if(!t[place].rightson)//右子树空，无元素
			return -1;
		else
			return search(t[place].rightson,x);
	}
	if(t[place].value>x)//去左子树找
	{
    
    
		if(!t[place].leftson)
			return -1;
		else
			return search(t[place].leftson,x);
	}
}

我们很容易发现，一次查找的复杂度与深度有关。在许多情况下，这颗二叉树会长的比较平均，这时深度仅为$lo{g}_{2}n$级别，复杂度仅为$O(logn)$。但是有些时候二叉树长得比较畸形，全往一侧倒，像下面这样。

那这时复杂度陡增至$O(n)$，显然不利于查找（当然后面的插入、删除、修改操作都变慢了）。因而我们就需要对二叉树进行一些处理。限于本文篇幅不在本文展开，将在后面的文章中提到一种splay的旋转树，使得树的结构始终保持平衡状态。

插入

为了实现这样一个数据结构，我们显然在插入的时候就得有点讲究。

对于一颗空树，显然乱放就好。

如果已经有一些数了呢？我们再想插入，应该怎么做呢？

很简单，和查找一样。

为什么？我为了查找的方便，必须要求这种左<中<右的结构，那么插入的时候就必然要满足这种结构，不能乱放。

我们就从根开始下放。如果比根大，那就往右放；如果比根小，那就往左放；如果对应的节点都空了，证明该放元素了，新增节点放上元素，过程停止。

如果某节点元素和待插入元素值相等，则直接出现次数+1，可以停止了。

例如我们还是对这颗二叉树进行操作。现在我们要向原二叉树中添加一个15，操作如下：

从根开始：

待插入元素15比7大，因而往右边放。

15>9，继续向右放。

15>12，15>14，连续两次向右放。因而到了16。

16既没有左儿子又没有右儿子。由于15<16，因而去访问16的左儿子，发现空了，因而应该新建节点了。此时整个过程结束。

然后就是代码时间，真的和查找很像：

void insert(int place,int x)//place为当前的节点编号，x为待插入元素值
{
    
    
	if(!tot)//二叉树为空，随意摆
	{
    
    
		t[place].value=x;
		t[place].father=-1;//父节点-1表示不存在
		return;
	}
	if(x<t[place].value)//小于枢轴元素，去左子树
	{
    
    
		if(!t[place].leftson)//没有左子树，该插入了
		{
    
    
			t[++tot].value=x;//tot为总的节点数。此时加一代表插入元素
			t[place].leftson=tot;//更新父节点的leftson
			t[tot].father=place;//新增节点的父节点更新
			return;
		}
		else
			insert(t[place].leftson,x);//有左子树，去左子树查
	}
	if(x>t[place].value)//大于枢轴元素，同理
	{
    
    
		if(!t[place].rightson)
		{
    
    
			t[++tot].value=x;
			t[place].rightson=tot;
			t[tot].father=place;
			return;
		}
		else
			insert(t[place].rightson,x);
	}

前驱与后驱

这个概念是有序结构中特有的。当某一个元素没有重复的时候，它的后驱为比它大的最小的数，前驱为比它小的最大的数。

这个概念在二叉树中很容易找到。

注意到我每次在画二叉树时有意的将子树越画越小，其实目的在这儿：

发现没：一个子树最左边和最右边其实就是这个子树的最小值和最大值！

因而，一个数的前驱，只需要在左子树不断找右儿子，直到找不到为止；一个数的后驱，只需要在右子树不断找左儿子，直到找不到为止。

例如：7的前驱，只需要找到5这颗子树的最右边节点即可，5->6，6即为7的前驱。思路非常简单。

代码如下：

int pre(int place)//找到place处的前驱
{
    
    
	int now=t[place].leftson;//去左子树找前驱
	while(t[now].rightson)//只要右儿子还在就往右儿子跑
		now=t[now].rightson;
	return t[now].value;
}
int next(int place)//找到place处的后驱，思路一样
{
    
    
	int now=t[place].rightson;
	while(t[now].leftson)
		now=t[now].leftson;
	return t[now].value;
}

删除

这是最麻烦的操作。

通常分以下三种情况。

1.没有儿子了。这种叶节点那删除了跟没删除差不多，树的结构不会发生变化。因而直接删除就行，父节点对应的左/右儿子别忘了清空。

这种图非常简单，因而省去。

2.只有一个儿子的。

那还不好办，直接把那唯一一个儿子拼上去就行，等同于链上删除一个节点，直接前后两个节点一配合孤立中间节点就行。

3.有俩儿子的。

任何一个子树不能没有根。这种情况的总体思想就是拿这个节点的前驱或者后驱来替代这个节点做根。这里采取后驱做新的根的操作，前驱操作同理。

这还得分两种小情况：

a.后驱不是右儿子。

那么我直接找到后驱就行。根据我们上述的定义，这里的后驱必然没有左儿子，那么这个节点删除就变成了前面两种简单的情况。

图如下：

后驱没儿子的。这种情况相当于做一遍1。

后驱只有右儿子的。这种情况相当于做一遍2。

注：虚线代表可能有若干层。

b.后驱就是右儿子。

那么我们上面这种操作就不成立了——右儿子都上了那现在的右儿子怎么办？那不就是成链了？操作等同于1！

看图：

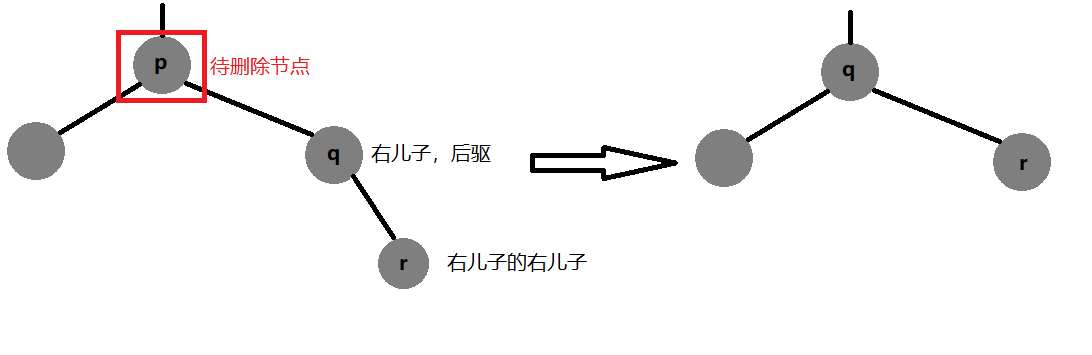
这个时候p、q、r相对关系成链状——没有其他节点掺和，因此直接删除就好。

附上代码（算法导论版）：

void transplant(int u,int v)//让v节点继承u节点信息的函数
{
    
    
	if(!t[u].father)//u为原树根
	{
    
    
		root=v;//树根为v
		return;
	}
	//更新u父亲关于u的信息
	if(u==t[t[u].father].left)//u为其父节点左儿子
		t[t[u].father].left=v;
	else
		t[t[u].father].right=v;//u为父节点右儿子
}
//注意到这里没有更新u子节点状态。在上文中我们其实可以发现，删除节点时子节点的子树状态没有改变，因而无需修改此处。
void delete_node(int u)//删除u节点
{
    
    
	if(!t[u].leftson)//无左儿子
		transplant(u,t[u].rightson);//右儿子继承
	else
		if(!t[u].rightson)//无右儿子
			transplant(u,t[u].leftson);//左儿子继承
		else//既有左儿子又有右儿子
		{
    
    
			int successor=next(u);//找到后驱，且必然存在
			if(t[successor].father!=u)//3.a情况
			{
    
    
				transplant(successor,t[successor].right);//那后驱的右节点更新
				t[successor].right=t[u].right;//继承u的子孙
				t[t[successor].right].father=successor;	//更新后驱的子孙
			else//3.b情况，同理
			{
    
    
				transplant(u,successor);
				t[successor].left=t[u].left;
				t[t[successor].left].father=successor;
			}
		}
}

这就是二叉树的删除操作。

优化

限于本文篇幅，这里不再讲解下篇文章中splay及其用法。我们前文提到了树往一边倒的问题，这会显著增大BST的运行时间。我们可以通过随机化二叉树来尽可能地平衡这颗树。当然最稳妥的方法还是splay，时刻让树转起来，这样才尽可能地平衡。