三维旋转矩阵推导及演示

推导过程

  设$v$是三维空间中任意向量，求$v$绕$n$顺时针旋转$\theta$所得到的向量$v^{\prime }$，其中$n$是单位向量，$n=\left[\begin{array}{c}{n}_x\\ n_y\\ n_z\end{array}\right]$，$n_x^2+n_y^2+n_z^2=1$。
  首先把$v$分解为垂直、平行于$n$的两个分量：$v_{\perp }=v-(v^{T}n)n$，$v_{||}=(v^{T}n)n$。
  不妨设$w=n\times v_{\perp }$，那么由叉积的定义可知，$w$与$n、v_{\perp }$垂直，方向服从右手法则，由于$n$是单位向量，$n$和$v_{\perp }$也互相垂直，所以$|w|=|v_{\perp }|$。设$v_{\perp }^{\prime }$为$v_{\perp }$绕$n$旋转$\theta$得到的向量，那么$v_{\perp }^{\prime }=v_{\perp }cos\theta +wsin\theta =[v-(v^{T}n)n]cos\theta +(n\times v)sin\theta$。
  由于平行分量旋转后没有变化，所以：$$v^{\prime }=v_{\perp }^{\prime }+v_{||}=[v-(v^{T}n)n]cos\theta +(n\times v)sin\theta +(v^{T}n)n$$
  令$v=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$，带入上式可得：
$$\begin{array}{rl}{v}^{\prime }& =\left(\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]-\left(\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\ast \left[\begin{array}{c}{n}_x\\ n_y\\ n_z\end{array}\right]\right)\left[\begin{array}{c}{n}_x\\ n_y\\ n_z\end{array}\right]\right)cos\theta +\left(\left[\begin{array}{c}{n}_x\\ n_y\\ n_z\end{array}\right]\times \left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]\right)sin\theta +\left(\left[\begin{array}{ccc}1& 0& 0\end{array}\right]\ast \left[\begin{array}{c}{n}_x\\ n_y\\ n_z\end{array}\right]\right)\left[\begin{array}{c}{n}_x\\ n_y\\ n_z\end{array}\right]\\ & =\left(\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]-n_x\left[\begin{array}{c}{n}_x\\ n_y\\ n_z\end{array}\right]\right)cos\theta +\left[\begin{array}{c}0\\ n_z\\ -n_y\end{array}\right]sin\theta +n_x\left[\begin{array}{c}{n}_x\\ n_y\\ n_z\end{array}\right]\\ & =\left[\begin{array}{c}1-n_x^2\\ -n_x{n}_y\\ -n_x{n}_z\end{array}\right]cos\theta +\left[\begin{array}{c}0\\ n_z\\ -n_y\end{array}\right]sin\theta +\left[\begin{array}{c}{n}_x^2\\ n_x{n}_y\\ n_x{n}_z\end{array}\right]\\ & =\left[\begin{array}{c}{n}_x^2(1-cos\theta )+cos\theta \\ n_x{n}_y(1-cos\theta )+n_{z}sin\theta \\ n_x{n}_z(1-cos\theta )-n_{y}sin\theta \end{array}\right]\end{array}$$
  令$v=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]$，带入上式可得(化简过程和上面差不多，就直接省略了)：
$$\begin{array}{rl}{v}^{\prime }& =\left[\begin{array}{c}{n}_x{n}_y(1-cos\theta )-n_{z}sin\theta \\ n_y^2(1-cos\theta )+cos\theta \\ n_y{n}_z(1-cos\theta )+n_{x}sin\theta \end{array}\right]\end{array}$$
  令$v=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$，带入上式可得：
$$\begin{array}{rl}{v}^{\prime }& =\left[\begin{array}{c}{n}_x{n}_z(1-cos\theta )+n_{y}sin\theta \\ n_y{n}_z(1-cos\theta )-n_{x}sin\theta \\ n_z^2(1-cos\theta )+cos\theta \end{array}\right]\end{array}$$
  将上述三个结果结合起来，可以得到一个$3\ast 3$的矩阵：
$$\begin{array}{rl}M& =\left[\begin{array}{ccc}{n}_x^2(1-cos\theta )+cos\theta & n_x{n}_y(1-cos\theta )-n_{z}sin\theta & n_x{n}_z(1-cos\theta )+n_{y}sin\theta \\ & & \\ n_x{n}_y(1-cos\theta )+n_{z}sin\theta & n_y^2(1-cos\theta )+cos\theta & n_y{n}_z(1-cos\theta )-n_{x}sin\theta \\ & & \\ n_x{n}_z(1-cos\theta )-n_{y}sin\theta & n_y{n}_z(1-cos\theta )+n_{x}sin\theta & n_z^2(1-cos\theta )+cos\theta \end{array}\right]\end{array}$$

演示过程

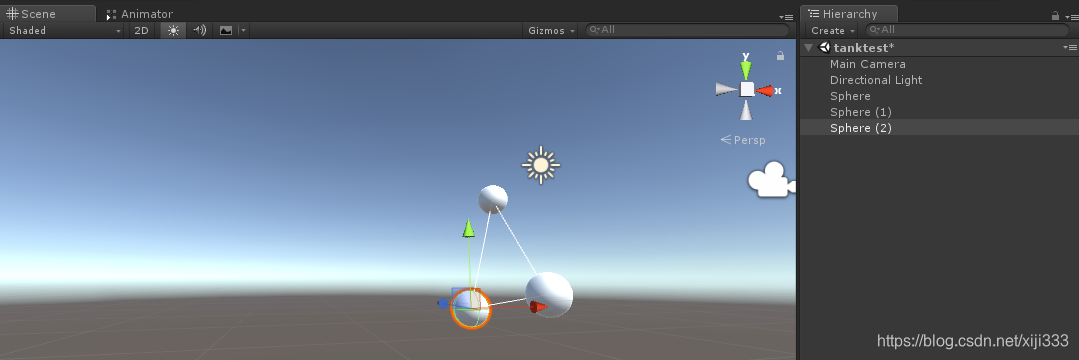
  为了有较为直观的演示效果，我决定使用$unity$进行演示。思路比较简单，随便选取一个向量作为旋转轴，然后在这个向量的起始和终点位置绘制两个球体，再使用第三个球体绕着这根轴旋转。同时在$scene$场景下绘制出这三个球体之间的连线，方便我们观看旋转效果。
  抛开绘制连线的部分，其实在代码中只需要修改运动球体的坐标即可。具体做法就是把球体的初始坐标或者说当前坐标作为向量，然后与这个矩阵相乘(相当于做变换)得到新的坐标，再把这个坐标当作球体的新坐标即可。
  那么这里就涉及到一个问题，坐标是行向量呢还是列向量呢，如果是前者那么需要左乘矩阵，否则需要右乘，我自己测试的结果是：左乘相当于顺时针旋转，右乘相当于逆时针旋转。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class move : MonoBehaviour {
    
    

	// Use this for initialization
	static Vector3 col1, col2, col3;
	void Start () {
    
    
		float angle = Mathf.PI/12;
		float c = Mathf.Cos(angle);
		float s = Mathf.Sin(angle);
		Vector3 A = new Vector3(1, 3, 4);
		A.Normalize();

		col1 = new Vector3(
			c + (1 - c) * A.x * A.x,
			(1 - c) * A.x * A.y + s * A.z,
			(1 - c) * A.x * A.z - s * A.y
			);

		col2 = new Vector3(
			(1 - c) * A.x * A.y - s * A.z,
			c + (1 - c) * A.y * A.y,
			(1 - c) * A.y * A.z + s * A.x
			);

		col3 = new Vector3(
			(1 - c) * A.x * A.z + s * A.y,
			(1 - c) * A.y * A.z - s * A.x,
			c + (1 - c) * A.z * A.z
			);
		Debug.Log(A.ToString("f4"));
		Debug.Log(col1.ToString("f4"));
		Debug.Log(col2.ToString("f4"));
		Debug.Log(col3.ToString("f4"));
	}
	// Update is called once per frame
	void FixedUpdate () {
    
    
		Vector3 pos = transform.position;
		//左乘
		//float x = pos.x * col1.x + pos.y * col1.y + pos.z * col1.z;
		//float y = pos.x * col2.x + pos.y * col2.y + pos.z * col2.z;
		//float z = pos.x * col3.x + pos.y * col3.y + pos.z * col3.z;
		//右乘
		float x = col1.x * pos.x + col2.x * pos.y + col3.x * pos.z;
		float y = col1.y * pos.x + col2.y * pos.y + col3.y * pos.z;
		float z = col1.z * pos.x + col2.z * pos.y + col3.z * pos.z;
		transform.position = new Vector3(x, y, z);
	}

	public void OnDrawGizmos()
	{
    
    
		Vector3 start = new Vector3(0, 0, 0);
		Vector3 end = new Vector3(1, 3, 4);
		Gizmos.DrawLine(start, end);
		Gizmos.DrawLine(transform.position, start);
		Gizmos.DrawLine(transform.position, end);
	}
}