SVM(support vector machine)最早是由Vladimir N.Vapnik 和 Alexey Ya.Chervonenkis在1963年提出,目前的版本(soft margin)是Corinna Cortes 和 Vapnik在1993年提出,1995年发表。深度学习(2012)出现之前,SVM被认为是机器学习中近十几年最成功表现最好的算法。
先看一个例子:
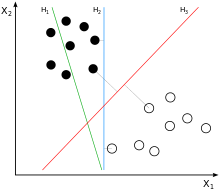
一个平面,里面有两类点,怎样画一条直线将两类点比较好的分开?很明显图中H1不能分开两类点,而H2和H3做到了。二维平面中可以用一条直线将两类分开,那扩展到N维的超平面呢?,SVM的主要内容就是找一个n维超平面将n维的两类样例分开,当一个新的n维点输入时根据其在超平面的哪一侧将其归为那一类。
以二维的情况来分析,从上图中我们可以看到,这样的直线可以有无数条,SVM要找到边际最大的一条来使用。那么边际是什么?下面介绍边际(margin)的概念。

画一条区分的分界线,计算两类样例中与之距离最近的点和分界线间的距离,两者距离之和就是边际。上图中第二幅的画法就能得到更大边际的分界线。为什么要选择边际最大的超平面呢?是为了新的测试点输入时可以根据在超平面哪一侧更准确的判断测试点是属于哪一类样例。
用于区分的超平面两侧可以经过最近的两个点再画两个超平面,分界超平面在与两侧超平面距离相等的中间。两侧的两个超平面平行。
在详细的讲SVM怎么建立边际最大的超平面MMH(Max Margin Hyperplane)之前,还要先介绍两种情况,线性可区分(linear separable)和线性不可区分(linear inseparable).
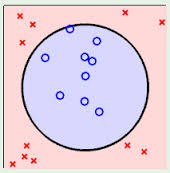
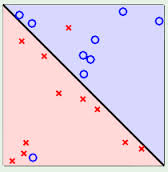
前面几张图的例子都是比较完美的例子,可以用一条直线来将两类样例分开,称为线性可区分,而如图的情况下就没办法直接用一条直线将两类样例分开,称为线性不可区分。后者更复杂,所以这里先讨论线性可区分的情况。
关于超平面的公式可以定义为:
W*X + b = 0
这里X是N维的训练样例
W是N维的权重 W = {W1, W2, W3, …, Wn}
b是偏向bias
就好比二维直线的方程式y = kx+b,这里只是扩展到N维,点的坐标是(X1,X2,X3,…,Xn),W就好比扩展到N维的斜率k.
图3中,假设二维的特征向量:X=(x1, x2) 超平面方程为:
W1*X1 + W2*X2 + b = 0
则所有超平面上方的点满足
W1*X1 + W2*X2 + b > 0
所有超平面下方的点满足
W1*X1 + W2*X2 + b < 0
将两类样例的分类标记classlabel分别用值+1和-1, 字母y表示,超平面两边边际的两个平行的超平面用H1和H2表示,令两侧边际线上的点代入结果=1和-1,则H1,H2外侧
H1: W1*X1 + W2*X2 + b >= 1 , y = +1
H2: W1*X1 + W2*X2 + b <= -1 , y = -1
综合以上两式,得到
y*(W1*X1 + W2*X2 + b) >= 1 公式(1) ,也就是说所有训练集的点都满足这个公式
SVM叫做支持向量机,那么什么是支持向量呢,所有坐落在边际H1,H2超平面上的点,也就是向量即被称为支持向量,可以看出支持向量最少是一边一个,当然也可以有很多个,只要它在边际线。
分界的超平面和H1,H2上任意一点的距离 = 1/(||W||) ||W||是向量的范数,则最大边际距离 = 2/(||W||)
SVM如何找到并使用最大边际的超平面(MMH)呢,这个过程比较复杂,需要通过一系列的数学公式和定义来推导,这里省去过程,直接给出结论:
上面公式(1)可变为有限制的凸优化问题,利用KKT条件和拉格朗日公式,就可以推导出MMH或者说“决定边界”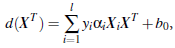
其中L是向量维度,Xi是支持向量点,XT是需要测试的实例,yi是支持向量Xi的分类标记,阿尔法i和b0是刚才一系列计算中得到的具体值。
通过这个公式,就可以对一个实例进行分类。当需要测试某个实例时,将其代入公式中,得到的结果通过其正负就可以对其进行分类,为正一类,为负则是另一类。
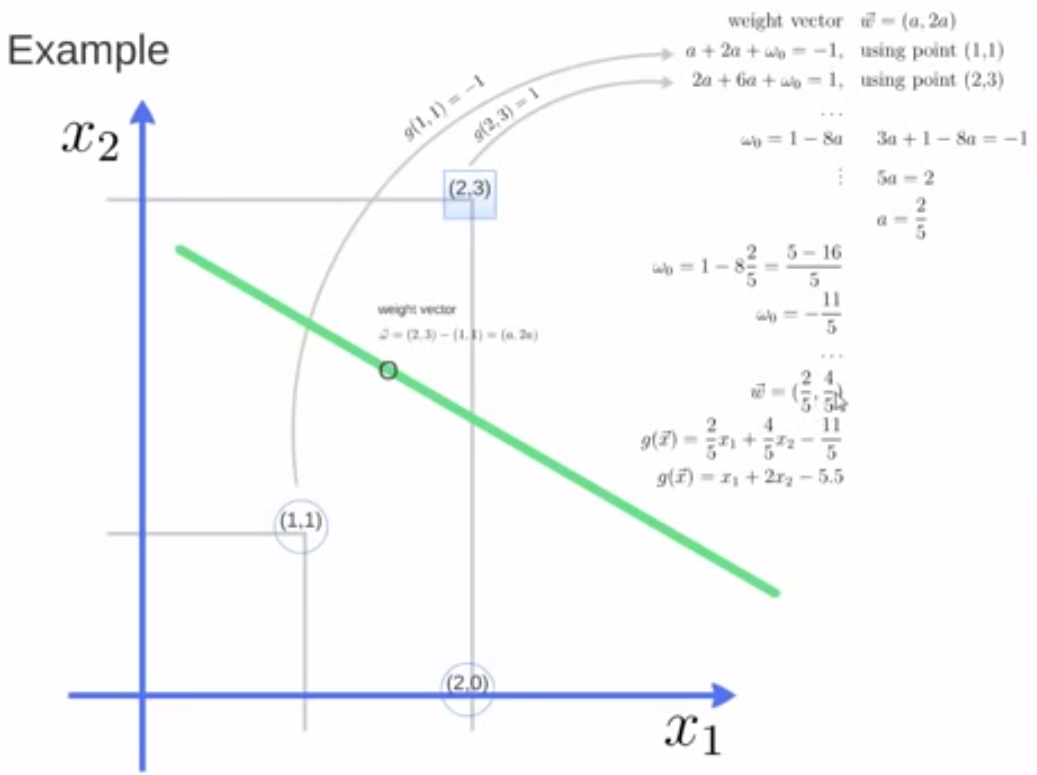
下面通过一个例子,熟悉SVM的计算过程。
如图,已知训练集(2,3), (1,1), (2,0)这三个点,(2,3)是第一类,(1,1), (2,0)是第二类,怎样进行SVM计算呢。
首先可以看出支持向量是(2,3)和(1,1),向量W =(2,3)-(1,1) = (a,2a)
根据公式两侧边际线上的点W1*X1 + W2*X2 + b = 1和-1, 可以列出
2*a + 3*2a + b = 1
1*a + 1*2a + b = -1
解得a = 0.4, b= - 2.2
则向量W为(0.4, 0.8)
g(向量x) = 0.4*x1 + 0.8*x2 - 2.2
通过这个方程就可以对平面中的点进行判断,凡是第一类的点也就是是分界线上方的点坐标代入,结果必然大于0,第二类的点代入结果必然小于0。这样也就建立了SVM的方程。
另外我们可以看出SVM可以解决两类实例的分类问题,但一般问题中,样例的类别往往不止两类,这时候SVM是怎么处理的的呢?比如有10类的样例,怎么进行分类判断?只需要建立10个SVM方程就能得到结果。比如第一个是类别1,第二个是类别2到10的集合这样就能建立一个SVM方程,第一个是类别2,第二个是类别1和类别3到10的集合这样建立第二个SVM方程,以此类推。
最后总结一下SVM的特点:
1.训练好的模型的算法复杂度是由支持向量的个数决定的而不是由数据的维度决定的,所以SVM不太容易产生overfitting。
2.SVM训练出的模型完全依赖于支持向量,即便训练集里所有非支持向量全部除去,训练出的模型也完全一样。
3.一个SVM如果训练得出的支持向量个数较少,SVM训练出的模型比较容易被泛化。可以适用于更多的例子,而如果支持向量过多,那么可能支持针对这个例子区分的比较好,其它情况区分的并不是很好。
下一篇通过Python对SVM进行实践。