机器学习笔记——支持向量机（SVM）上

支持向量机（Support Vector Machine, SVM）

---

1、算法的基本思想

在机器学习算法中，分类问题最基本的想法就是基于训练集D在样本空间中找到一个划分超平面，将不同类的样本分开，但是这样的超平面很多，如何选择“合适的”超平面是我们应当需要考虑的。

如上图的二维空间中划出的三条超平面($H_1，H_2，H_3$)，显然将$H_3$作为分类的超平面最为合适，其具有较强的鲁棒性和泛化能力。可是这样划分的理论依据又是什么呢？

2、支持向量机的理论依据

在样本空间中，我们可以以如下的线性方程来描述一个超平面$(w,b)$：

$$w^Tx+b=0（2.1）$$
其中 $w$为超平面的法向量（即与超平面垂直的向量），其决定了超平面的方向， $b$为位移量，决定了超平面与原点之间的距离，样本空间中任意一点 $x$到超平面 $(w,b)$的距离为：
$$r=\frac{|w^T+b|}{||w||} (2.2)$$
$(figure2.1)$
设：
$$\begin{cases} y_i=+1, & \text{对于所有的蓝点} \\ y_i=-1, & \text{对于所有的红点} \end{cases} (2.3)$$
则有
$$\begin{cases} w^Tx+b>0, & \text{$y_i=+1$} \\ w^Tx+b<0, & \text{$y_i=-1$} \end{cases} (2.4)$$
如果我们要求再高一点，假设决策面正好处于间隔区域的中轴线上（如图中所示黑色实线），并且相应的支持向量对应的样本点到决策面的距离为 $d$，那么公式 $(2.4)$就可以进一步写成：
$$\begin{cases} \frac{w^Tx+b}{||w||}≥d, & \text{$y_i=+1$} \\ \frac{w^Tx+b}{||w||}≤-d, & \text{$y_i=-1$} \end{cases} (2.5)$$
将 $(2.5)$式中左右两边同时除以 $d$，并令 $\frac{w^T}{||w||d}={w_s}^T$， $\frac{b}{d}=s$，则可得：
$$\begin{cases} {w_s}^Tx+s≥+1, & \text{$y_i=+1$} \\ {w_s}^Tx+s≤-1, & \text{$y_i=-1$} \end{cases} (2.6)$$
其实， ${w_s}^T+s=0$与 $w^Tx+b=0$为同一直线（或超平面），则式 $(2.6)$又可写成
$$\begin{cases} w^Tx+b≥+1, & \text{$y_i=+1$} \\ w^Tx+b≤-1, & \text{$y_i=-1$} \end{cases} (2.7)$$

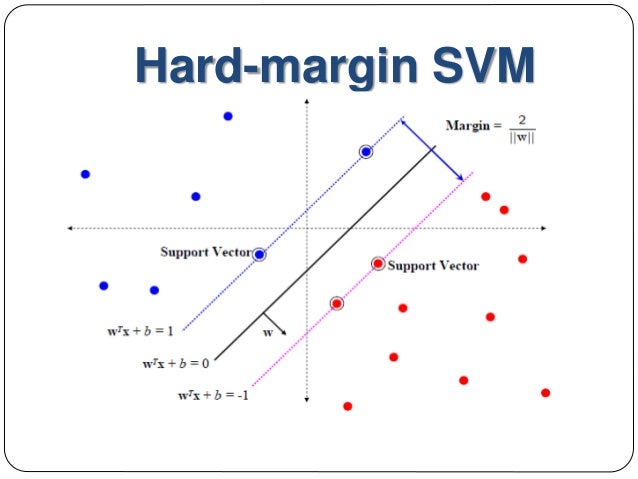
如图$figure2.1$所示，离超平面最近的点称为“支持向量”，两个异类支持向量到超平面的距离之和为：

$$d=\frac{w^Tx_i+b}{||w||}+\frac{w^Tx_t+b}{||w||} (2.8)$$
其中 $x_i$和 $x_t$为支持向量，他们满足 $w^Tx_i+b=1$和 $w^Tx_t+b=-1$
故：
$$d=\frac{2}{||w||} (2.9)$$
我们知道当 $d$取得最大值时，超平面恰好属于两类样本点的正中间，此时能较好的划分两类样本，因此问题转化为求参数 $w$和 $b$在何时的取值使得 $d$的值最大
显然当 $\frac{1}{||w||}$在约束条件 $y_i(w^Tx_i+b)≥1$的约束条件下取最大值的时候 $d$可取最大值，问题也可转化为求
$$求\frac{1}{2}||w||^2在约束条件y_i(w^Tx_i+b)≥1下的最小值$$
这就是支持向量的基本型。
如何解决这一问题，过程涉及高等数学中的拉格朗日乘子法来解决，在此不予详细说明，感兴趣的读者可自行查阅书籍。

3、在Python中使用SVM进行分类

from sklearn import svm
X = [[2, 0], [1, 1], [2,3]]
y = [-1, -1, +1]
clf = svm.SVC(kernel = 'linear')
clf.fit(X, y)  
print clf
# get support vectors
print clf.support_vectors_
# get indices of support vectors
print clf.support_ 
# get number of support vectors for each class
print clf.n_support_ 
a = clf.predict([[3,3]])
print(a)