研究算法的目的就是以设计时间复杂度更小的算法,但要想对算法进行优化必须学会计算每一个步骤的算法大小,进而从中寻找可以缩减的位置。为了计算每一步,有必要掌握一些基本的数学知识,有句话说过:数学水平在一定程度上决定了计算机的高度。
对于大多数算法而言,都应用到了for/while循环。在循环不断进行的过程中,每次运行循环体内基本操作的执行次数都是不同的。想要将每一次的结果相加,就相当于是不规则数的相加,也就是“求和”。同时,大多数算法使用递归方法,虽然递归有很多隐形的坏处,但是表达十分清晰,也常常被使用。给定递归式,寻找到所需总时间和输入N的关系,也是十分重要的。对数学能力的要求也是非常高的。下面从上文提及的两方面展开,分别谈论所需要的一些数学知识。
2.1集合,关系和函数
集合是数学中基础的概念,在集合之上定义了很多集合的操作(交,并,补)。以集合为基础设计的算法也有很多,例如:并查集(克鲁斯卡尔算法求解最小生成树)等等。关系是以集合依据的,多说一个在集合上的关系。关系的内容也有很多,例如等价关系,传递关系等等。相对详细的内容可以在离散数学中学到。函数可以理解成一种二元关系(x和y之间),一定是每一个x,有一个y与之对应,否则不可以被称作函数。根据像和原像的关系,函数还可以被分为单射(所有x都有对应且对应不同的y),满射(所有的y都具有原像),同时满足单射和满射的叫做双射。
2.2证明
证明是算法中很常见的考察方法,例如课后题中就包括很多时间复杂度的证明。在学习算法之前,我们已经学习了离散数学。我认为离散数学的一个教学目标就是教如何使用符号做证明,使证明过程更清晰易懂。证明的方法大概可以分成五种:
1)直接证明法:从现有条件出发,使用定理或者公理,最终得出想要的结论。直接证明也有两种方向,可以从条件证结论,也可以从结论证条件。要求过程中的每一个步骤都必须是充要条件。
2)间接证明法:证明原来命题的逆否命题成立。或者从中间出发,向两头延伸,最终得到条件和结论。
3)反证法:是一种常用的证明方法,当结论有明显的一个方向的倾向时可以使用反证法。假设结论不成立,推导和条件之间的矛盾。
4) 反例证明法:反例证明法往往用于结论已经明确。举出一个错误不满足明确的关系,即可证明。大多数情况下,反例很难被列举出来。
5)数学归纳法:数学归纳法常用于正确结论已经知道,但是需要详细的过程进行推导。具有相对固定的模板,已知n=1时成立,假设n=k时成立,通过n=k式子的变形推导出n=k+1也同样成立。
2.3对数
在算法分析中很多时间复杂度是和和㏒n有关的(在计算机中所有的对数函数的都是以2为底的),关于对数有计算公式如下:
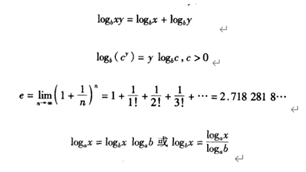
2.4顶函数与底函数
在算法中常常会对整数做除以2的操作,但此时如果不知道整数的奇偶性,就会出现小数。为了进一步明确范围,会使用顶函数和底函数。顶函数是大于等于x的最小整数,底函数是小于等于x的最大整数。
关于顶函数和底函数有以下重要等式:
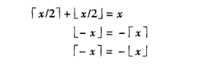

2.5阶乘和二项式系数
阶乘来源于排列,表示第一个位置有多少种排法,进而第二个位置有多少种排法,依此类推。常用大写P表示,阶乘的时间复杂度是很高的,经常的表示公式为:

二项式系数来源于组合。组合即不考虑顺序,是阶乘的推广。重要的是组合数公式:
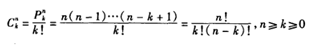
2.6鸽巢原理
鸽巢定理讲的是一定分配的必然性,比如十一只鸽子进入十个洞穴,必然至少有两个鸽子在其中一个洞穴。从至多至少两个角度,可得如下公式:

2.7和式
和式有以下公式:


当被加式子不再只取整数,而变成一个函数时,需要使用积分的知识求解。可以使用不等式来确定上下界,当左右两式达到相同的数量级时,就证明了时间复杂度。
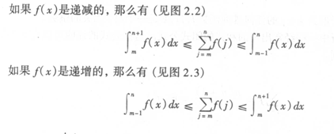
2.8递推关系:
递推关系用于计算递归函数的时间复杂度,分为以下几类:
对于齐次和非齐次的定义是由如下式子决定的:

1)线性齐次递推式(实例见书P53页):

2)非齐次递推关系(实例见书P55页):
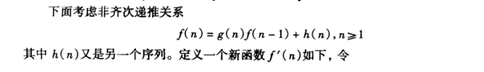
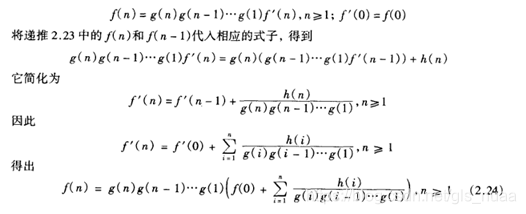
3)分治递推关系:
在算法中,对很多大规模都会采用分治思想,将时间复杂度不断细分再将更小规模整合,其中二分法是最常见的。

分治递推关系主要有三种方法求解:
(1)展开递推式(具体见书P57):
将递推式不断展开,直到某已知项,多为f(1)/f(0)。但展开递推式存在若干缺点:有些情况下耗时,呆板,也容易出现计算错误。
(2)代入法(具体见书P59)
这种方法,通常用来证明上下界,也可证明精确解。需要猜想一个解,结合数学归纳法求出所设的参数值。对于猜想的解是依靠经验或者之前学过的一些定理或者推论。
(3)更换变元(具体见书P62)
更换变元可以是用指数函数代替原来的分子分母式,尽力转化成前面齐次的形式在进行求解。