数据结构（十五）——堆与堆排序及时间复杂度分析

文章目录

前言
堆（Heap）

堆是什么
为什么要使用堆
堆的实现及时间复杂度分析

堆的类声明
堆的插入方法
堆的删除方法
初始化堆

堆排序

前言

上一篇数据结构文章分析了二叉树的实现及其遍历方法，学习了树形结构。但当时我没有思考为什么要学习树形结构这个问题。这篇堆和堆排序是二叉树的应用分析，回答了这个问题。

堆（Heap）

堆是什么

堆是一颗有最大堆和最小堆之分 / 在最大堆中每个节点的值都大于等于其子节点(如果有子节点的话)的值 / 最小堆定义类似 / 的完全二叉树。

堆的基本操作包括初始化堆，插入堆，获取堆元素，删除堆。其中获取和删除操作只能依次获取堆中优先级最高的元素。

为什么要使用堆

首先我们要了解什么是优先级队列，也就是本章的标题。

优先级队列：FIFO的队列和FILO的栈，元素的pop()顺序由元素进入队列的顺序决定。而优先级队列，元素pop()的顺序由元素的优先级决定。可以按优先级递增，也可以是优先级递减。也就是说元素输出的顺序和元素进入的顺序无关。

堆属于优先级队列，虽然优先级队列有队列两个字，但优先级队列和队列完全是两个不同的概念和层级。千万不能以为是从属关系。

如果我现在有一个将n个元素按其优先级输出的需求。可以考虑以下三种存储结构。

数组
链表
二叉树

对于数组，插入操作花费时间为O(1), 获取优先级最高的元素所需时间为O(n),因为要遍历n个元素确定优先级最高的元素。
对于链表，与数组的操作时间相同。
对于二叉树，我们维护一个堆，插入和依次获取元素的时间复杂度皆为O(logn),我将在下面的内容中进行解释。

在这个需求中，无疑是堆的综合性能表现最好。这便是堆的价值之一。

堆的实现及时间复杂度分析

因为堆是一颗完全二叉树，特别适合用数组实现，所以以下是用数组实现的一个最大堆（MaxHeap）。

堆的类声明

template <class T>
class MaxHeap
{
public:
    MaxHeap(int theMaxSize = 10);
    ~MaxHeap(){delete [] heap;};
    int empty() const {return CurrentSize == 0;}
    int Size() const {return CurrentSize;}
    const T& top() const // 引用返回，不能作为左值，第二const表示不能修改类成员变量
    {
        if(CurrentSize == 0)
            throw OutOfBounds();
        return heap[1];
    }
    const T& pop();
    void push(const T& theElement);
    void initialize(T *theheap, int theSize);


private:
    int currentSize;
    int maxSize;
    T* heap;
};
template class<T>
MaxHeap<T> :: MaxHeap(int theMaxSize)
{
    currentSize = 0;
    maxSize = theMaxSize;
    heap = new T[MaxSize + 1];
}

堆的插入方法

template class<T>
void MaxHeap<T> :: push(const T& theElement)
{
    if(currentSize == MaxSize)
        throw "have no memory";

    int currentNode = ++currentSize;

    while(currentNode != 1 && theElement> heap[currentNode/2])
    {
        heap[currentNode] = heap[currentNode/2];
        currentNode /= 2;
    }
    heap[currentNode] = theElement;

}

时间复杂度：

将元素插入最后一位，再进行向上冒泡，即如果父节点的值小于被插入的元素，父节点下移，被插入的元素上移。时间复杂度取决于树的高度h。而完全二叉树的树的高度为[logn+1]的上取整，所示时间复杂度为O(logn)。

堆的删除方法

template class<T>
const T& MaxHeap<T> :: pop()
{
    if(currentSize == 0)
        throw "the heap is empty.";

    T res = heap[1];
    delete heap[1];

    T lastElement = heap[currentSize--];

    int p = 1; // p可以被 child/2代替，但会多执行几次计算
    int child = 2;

    while(child <= heapSize)
    {
        if(child < heapSize && heap[child] < heap[child+1]) //child < heapSize避免了溢出
            child++;

        if(lastElement >= heap[child]) // 不需要重构堆
            break;

        heap[p] = heap[child];
        p = child;
        child *= 2;
    }
    heap[p] = lastElement;

    return res;
}

时间复杂度：

删除操作的逻辑为，删除堆的根节点，将最后一个节点补到根节点位置，得到一颗不符合规则的堆。再对根节点进行向下冒泡，即如果父节点小于某一孩子或所有孩子，将元素值最大的孩子与父节点交换。孩子上移，父节点下移，下移后与孩子重复该操作，直到比孩子都大或没有孩子。
删除操作向下冒泡，操作时间还是取决于树的高度，时间复杂度为O(logn)

初始化堆

template<class T>
void :: MaxHeap<T> initialize(T* theHeap, int theMaxSize，int theCurrentSize)
{
    // 把原有的大根堆删掉
    delete [] heap;
    heap = theHeap;
    maxSize = theMaxSize;
    currentSize = theCurrentSize;

    for(int root = currentSize /2 ; root >= 1; root--) //在完全二叉树中，最后一个具有孩子的节点为n/2
    {
        T rootElement = heap[root];
        int child = root*2;

        while(child <= heapSize) //执行和删除操作中相同的向下起泡过程
        {
            if(child < heapSize && heap[child] < heap[child+1])
                child++;
            if(rootElement >= heap[child])
                break;

            heap[child/2] = heap[child];
            child *= 2;
        }

        heap[child/2] = rootElement;
    }
}

时间复杂度:

初始化堆的逻辑为，给你一个未按规则排序的数组，进行原地重排使之符合堆的要求。具体操作为找到最后一个拥有孩子的节点，在完全二叉树中位置为[n/2]详细取整。对该节点和之前的节点进行遍历，每次遍历执行向下冒泡操作。

因为有n/2个元素需要执行和删除相似的操作，所以时间复杂度乍一看应该是O(nlogn)。但是，并不是每个元素都需要时间为O(h)的向下冒泡操作。

实际上，只有根节点向下冒泡的操作所需时间为O(h)，根节点的孩子节点所需时间为为O(h-1),第i层节点的向下冒泡操作时间为O(h-i)。

根据完全二叉树的性质，第1层的节点数为1，第二层为2，第i层最多为2^(i-1)。

将每层的节点数与要操作的次数相乘再求和，可得
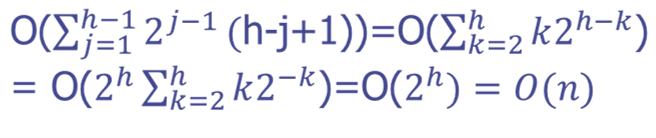
在这里插入图片描述
其中k/2^k的求和是高中的一个知识点，将和式乘1/2得到另一等式，再交叉相减便可解出。

综上，初始化堆的时间复杂度为O(n)

堆排序

如果将优先级看作元素的大小，对数组进行堆的初始化操作再依次删除取出元素，便可得到排好序的数组。


template class<T>
void MaxHeap<T> :: deactivate()
{
    heap = NULL;
}

template <class T>
void heapSort(T a[], int n)
{
    maxTeap<T> heap(1); // 首先利用构造函数建立最大堆
    initialize(a, n); // 堆的初始化

    // 通过删除从最大堆中提取元素
    for(int i = n-1; i>=1; i--)
    {
        a[i+1] = heap.pop();
    }
    heap.deactivate(); //从堆的析构函数中保存数组a，heap等于空，析构函数调用了个寂寞
}

时间复杂度

初始化堆的时间复杂度为O(n)
n-1次删除操作的时间复杂度为O(nlogn)
所以总操作时间复杂度为O(nlogn)

但是如果像初始化堆那样分析，每删除一个元素，总元素减一。
n-1次删除操作，操作时间应该为log(n)+log(n-1)+…+log(3)+log(2) = log(n!)。
且(n/2)^(n/2) ≤ n！≤ n ^ n,即 1/4*nlog(n) ≤ n! ≤ nlogn。常数可舍去，时间复杂度仍为O(nlogn).

多说一句：
堆排序是数据结构复习到现在第一个最坏时间复杂度为O(nlogn)的通用排序算法，优于插入、冒泡、选择这些基本排序方法。且比基数排序和箱子排序适用范围广。