矩阵知识：特征值&特征向量

一、特征值&特征向量

1.1 直观印象

如果把矩阵看作是运动，对于运动而言，最重要的是运动的速度和方向，那么：

• 特征值就是运动的速度
• 特征向量就是运动的方向

既然运动最重要的两方面都被描述了，特征值、特征向量自然可以称为运动（矩阵）的特征。

注意：由于矩阵是数学概念，非常抽象，所以上面所谓的运动、运动的速度、运动的方向都是广义的，在现实中有不同的替代。

1.2 几何意义

在下面的图中画出了基和向量（在 $\overrightarrow{i},\overrightarrow{j}$为基的空间里有向量 $\overrightarrow{v}$）

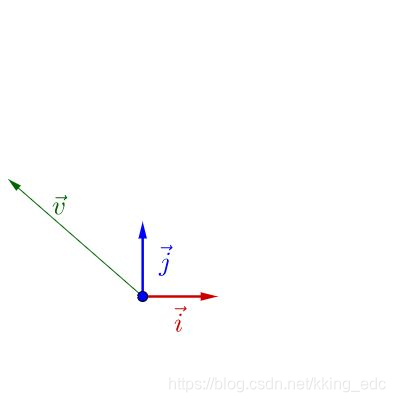
随便左乘一个矩阵A，图像看上去没什么特殊的：

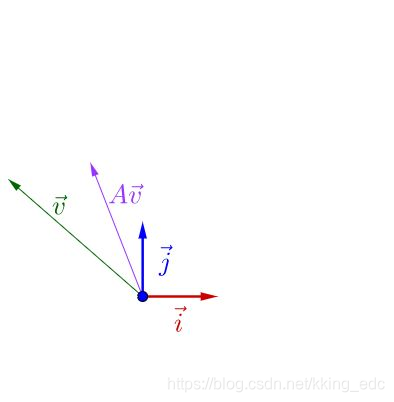
这时如果调整下 $\overrightarrow{v}$的方向，图像看上去就有点特殊了

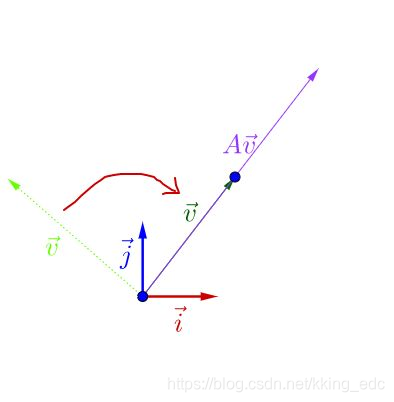
我们可以观察到，调整后的 $\overrightarrow{v}$和 $A\overrightarrow{v}$在同一根直线上，只是 $A\overrightarrow{v}$的长度相对 $\overrightarrow{v}$变长了，我们就称 $\overrightarrow{v}$是A的特征向量，而 $A\overrightarrow{v}$的长度是 $\overrightarrow{v}$的长度的 $\lambda$倍， $\lambda$就是特征值。从而，特征值和特征向量的定义如下：

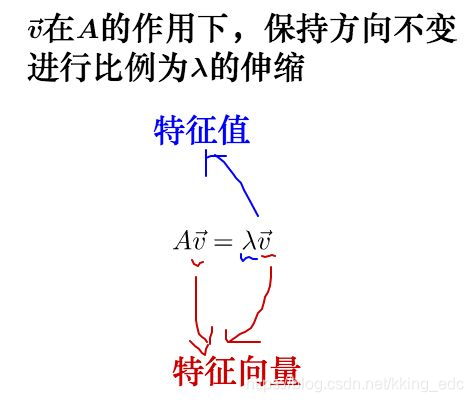
其实之前的A不止一个特征向量，还有另一个特征向量：

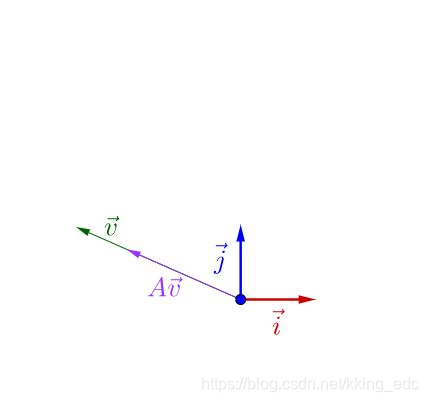
可以看出这两个特征值一个大于1一个小于1.
从特征向量和特征值的定义还可以看出，特征向量所在直线上的向量都是特征向量。

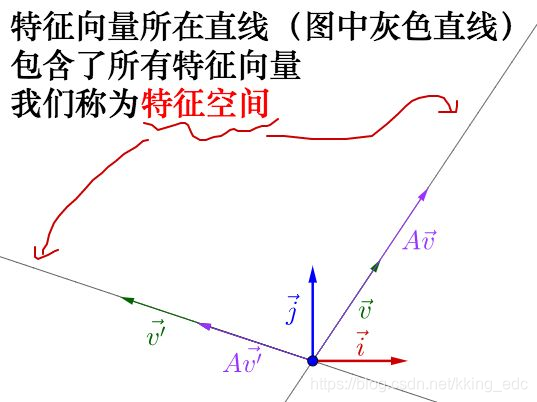
1.3 运动的速度和方向

一般来说，矩阵我们可以看作某种运动，而二维向量可以看作平面上的一个点（或者一个箭头）。对于点我们是可以观察的，但是运动我们无法直接观察。

就好像，跑步这个动作，我们不附加到具体的某个事物上是观察不到的，我们只能观察到：人跑步、猪跑步、老虎跑步,…，然后从中总结出跑步的特点。

从以上例子来理解矩阵，要观察矩阵代表的运动，需要把它附加到向量上才能观察出来。

首先进行一次乘法：

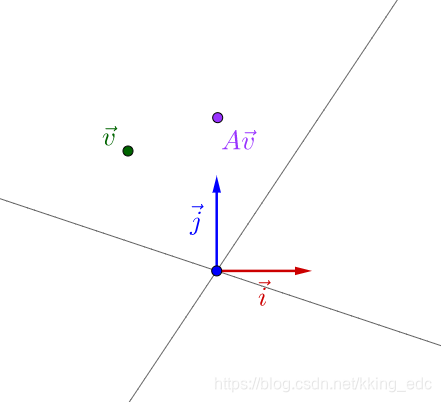
这个看不出明显的规律，如果进行多次乘法：

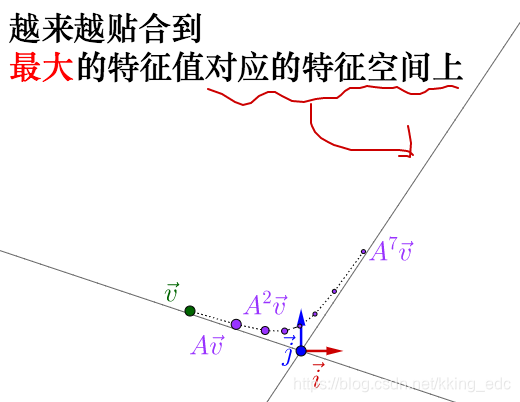
这个时候矩阵所代表的运动的最明显的特征，即速度最大的方向，就由最大特征值对应的特征向量展现了出来。

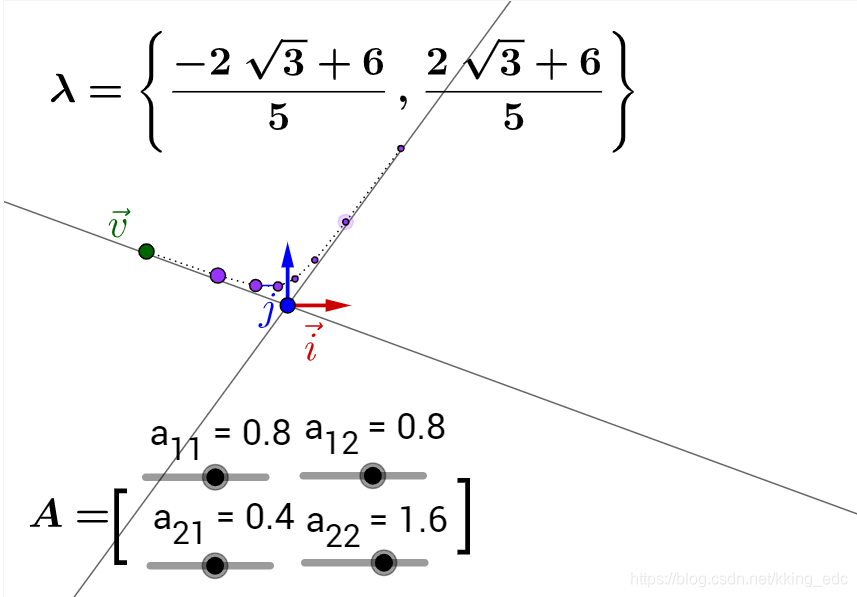
（对于复数的特征值、特诊向量，在上面就没有画出特征空间，但可以观察到反复运用矩阵乘法的结果是围绕着原点在旋转，关于复数特征值和特征向量在这里没有展开说）

1.4 特征值分解

我们知道，如果矩阵A可对角化的话，可以通过相似矩阵进行如下的特征值分解：
$A=P\Lambda P^{-1}$
其中 $\Lambda$为对角阵，P的列向量是单位化的特征向量，以下是一个具体的例子：

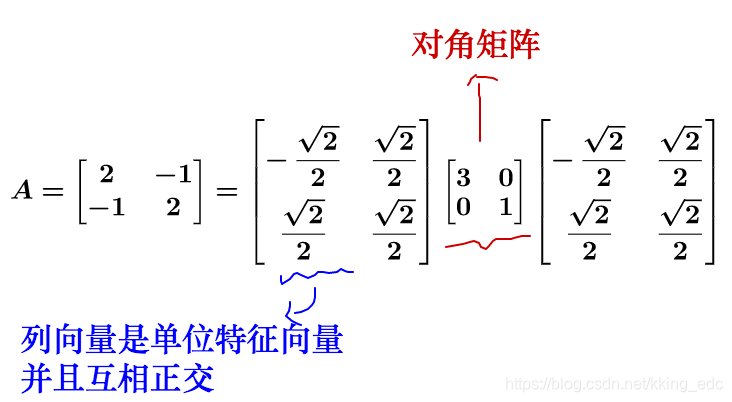
对于方阵的乘法，矩阵不会进行维度的升降，所以矩阵代表的运动实际上只有两种：

• 旋转
• 拉伸

最后的运动结果就是这两种的合成。

我们回头看下刚才的特征值分解，实际上把运动給分解开了：

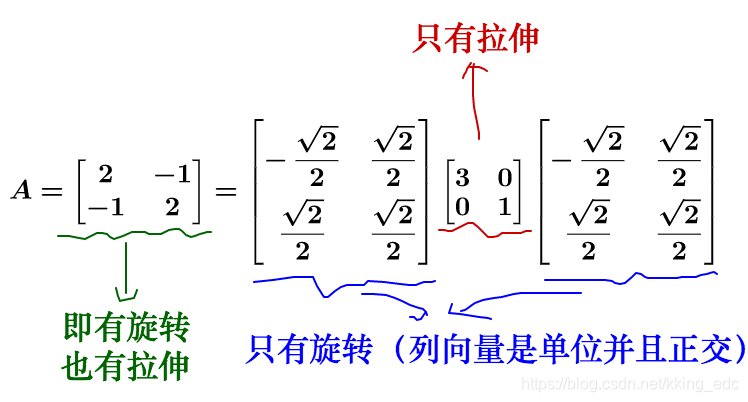
然后看下在几何上的表现：
假如存在这样一对单位特征向量，然后有着在这样一对特征向量下的正方形：

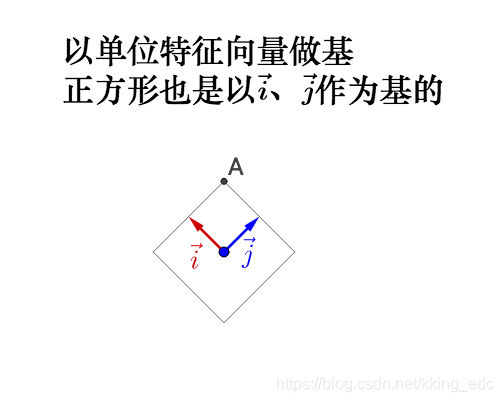
此时左乘P：

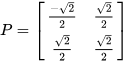
可以得到：

注意：
如果旋转前的基不正交，旋转后变成了一个不正交的标准基，那么实际会产生伸缩，所以之前说的正交很重要。
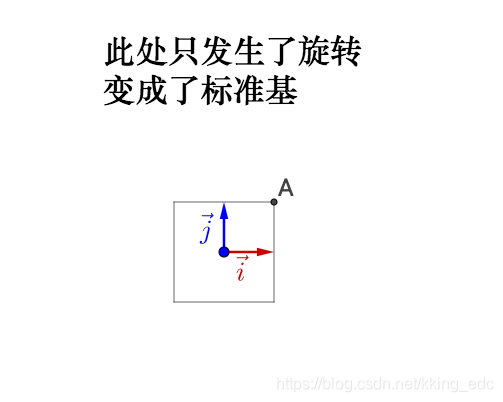
继续左乘对角矩阵：

可以得到：

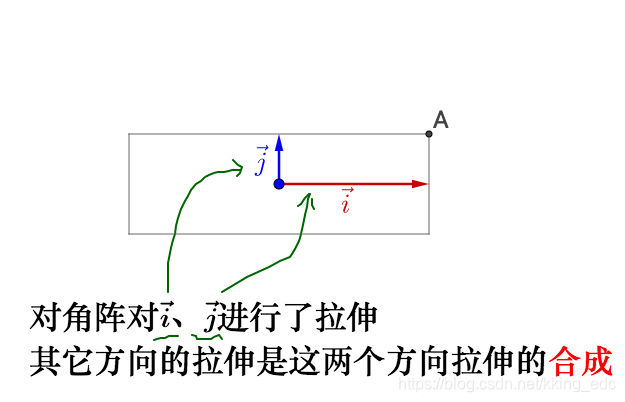
相当于，之前的旋转指明了拉伸的方向，所以我们理解了：

• 特征值就是拉伸的大小
• 特征向量指明了拉伸的方向

回到之前所说的运动，特征值就是运动的速度，特征向量就是运动的方向，而其余方向的运动就由特征向量方向的运动合成。所以最大的特征值对应的特征向量指明了运动速度的最大方向。

但是注意，上面的推论有一个重要的条件，这个条件就是特征向量正交，这样变换后才能保证变换最大的方向在基方向。如果特征向量不正交就有可能不是变化最大的方向，比如：

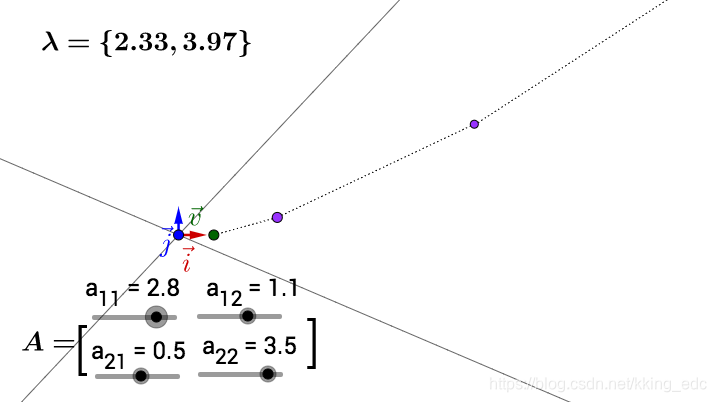
所以我们在实际应用中，都要去找正交基。但是特征向量很有可能不是正交的，那么我们就需要奇异值分解（在这里不展开）。

https://www.matongxue.com/madocs/228.html

1.5 关于特征值的计算

已知n阶矩阵A的特征值为 $\lambda_1,\lambda_2,...,\lambda_n$， $p(x)$为x的多项式，则P(A)的特征值为：

$p(\lambda_1),p(\lambda_2),...,p(\lambda_n)$