如何用快排思想在 O(n) 内查找第 K 大元素

如何用快排思想在 O(n) 内查找第 K 大的值

核心思想

快排核心思想就是 分治 和分区，可以用分区的思想来解答：在 O(n) 时间复杂度内求无序数组中的第 K 大元素。比如，4，2，5，12，3 这样一组数据，第 3 大元素就是 4。

可以选择数组区间 A[0…n-1] 的最后一个元素 A[n-1] 作为 pivot，对数组 A[0…n-1] 原地分区，这样数组就分成了三部分，A[0…p-1]、A[p]、A[p+1…n-1]。(当然 pivot 的选择还可以优化，这里我们只用其中的一种方式)

如果 p+1 = K，那 A[p] 就是要求解的元素；如果 K > p+1；说明第 K 大元素出现在 A[p+1…n-1] 区间，再用递归的思路在 A[p+1…n-1] 这个区间内查找。同理，如果 K < p+1,就在 A[0…p-1] 区间查找。

为什么上述解决思路的时间复杂度是 O(n)?

第一次分区查找，需要对大小为 n 的数组执行分区操作，需要遍历 n 个元素。第二次分区查找，只需要对大小为 n / 2 的数组执行分区操作，需要遍历 n/2 个元素。依次类推，分区遍历元素的个数分别为 n、
n/2、n/4、n/8、n/16…直到区间缩小为 1。

若把每次分区遍历的元素个数加起来，就是：n + n/2 + n/4 + n/8+…+1。这是一个等比数列求和。

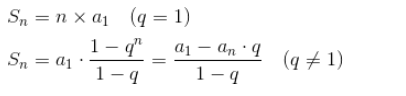
根据公式最后的和等于 2n - 1。所以时间复杂度就是 O(n)了。

另外，大多情况下我们可能会先这样想：每次取数组中的最小值，将其移动到数组的最前面，然后在剩下的数组中继续找最小值，依次类推，执行 K 次，找到的数据不就是第 K 大元素吗？

虽然这样确实可以实现，但是时间复杂度并不是 O(n)了，而是 O(K * n) 。虽然我们说，时间复杂度前面的系数可以忽略，那不就等于 O(n) 吗？

这个并不能这样理解。当 K 是比较小的常量时，比如 1，2，那最好时间复杂度确实是 O(n)；但当 K 等于 n/2 或者 n 时，这种最坏情况下的时间复杂度就是指数级的 O(n^2) 了。

详细代码

import java.util.*;

public class Finder {
	public int findKth(int[] a, int n, int K) {
		return findKth(a,0,n-1,K);
	}

	public int findKth(int[] a, int low, int high, int K) {
		int part = partation(a,low,high);
		if (part - low + 1 == K) {
			return a[part];
		} else if (part - low + 1 < K) {
			return findKth(a, part+1, high, K-part+low-1);
		} else {
			return findKth(a, low, part-1, K);
		}
	}
	
	public int partition(int[] a, int low, int high) {
		int key = a[low];
		while (low < high) {
			while (low < high && a[high] <= key) {
				high--;
			}
			a[low] = a[high];
			while (low < high && a[low] >= key) {
				low++;
			}
			a[high] = a[low];
		}
		a[low] = key;
		return low;
	}
}