Java实现二分法、牛顿(Newton)迭代法、快速弦截法方程求根的数值方法

问题场景

假定在一次实际的建筑设计中，伟大的设计师经过一波辛苦的操作终于得到一个最终的函数 $f(x)$，只需要求出这个函数 $f(x)$的零点，就可以完成整个项目的设计：
$y=f\left(x\right)=x^2+lnx,(x>0).$
对于这个问题很难入手，用一般的求解方式此时也是心有力而力不足，而这个解对整个工程又很重要，精度要求高，于是望着这个可爱的函数，心里暗自不爽…

问题引入

虽然上述的场景有点不符合实际，但是在真正的实际工程中，对于这种问题是真实存在的，而且实际的函数肯定比上述的函数 $f(x)$复杂得多。
这里我们就以 $y=f\left(x\right)=x^2+lnx,(x>0).$为研究对象，来了解一下对于这类问题的算法。
话不多说，直接利用数学工具得到函数图像：

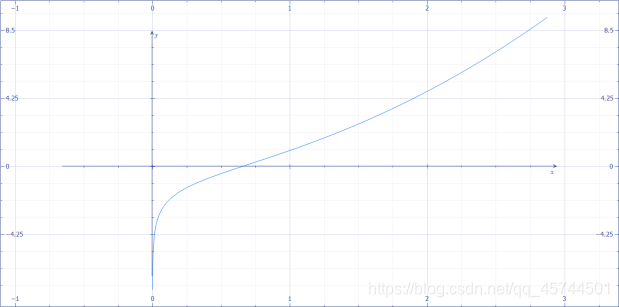
可以很清晰地看到该函数在其定义域上存在唯一的实数解，在区间 $(0,1)$中。

二分法

简介

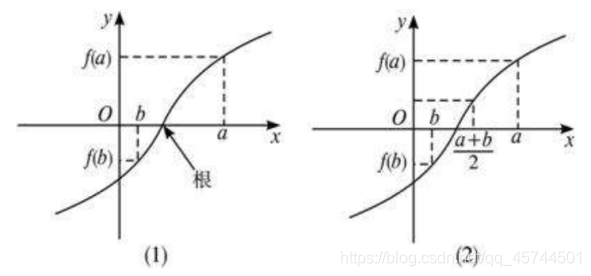
二分法，顾名思义，平均分成两份，实际是对于一个函数在一个特定的区间 $[a,b]$中单调，并且 $f(a)f(b)<0$,则一定
$\exists\xi\in\left(a,b\right),\mathrm{使得}f(\xi)=0$
通过 $f(a)f(b)<0$这一条件，不断对区间进行二分缩短，直到区间长度小于给定的最大允许区间长度（换句话说就是精度） $\varepsilon$,经过不断地迭代，可以使得精确解在一个极小的区间内，这样我们可以用区间的端点来作为函数的零点。
这是一个有效的求解方法，理论上是可以求得任何精度要求下的解，不过他的收敛速度缓慢，需要进行大量的计算才能得到结果。当然这也是针对精度要求高的条件下的情况，对于最开始就是很大的区间，使用二分法可以很快速的将区间缩短，并且计算的代价也比较小。

算法描述

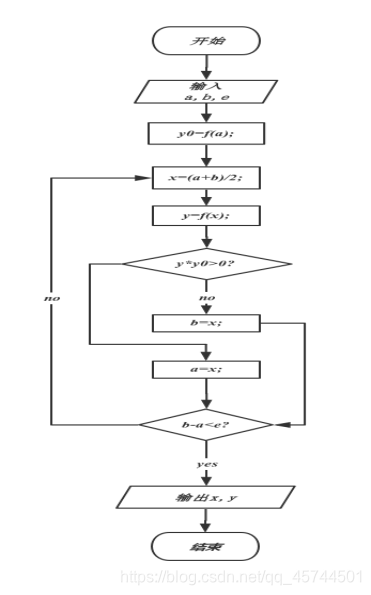
变量说明

$a$:给定区间下限
$b$:给定的区间上限
$e$ :给定的允许最大区间长度

程序运行结果截图

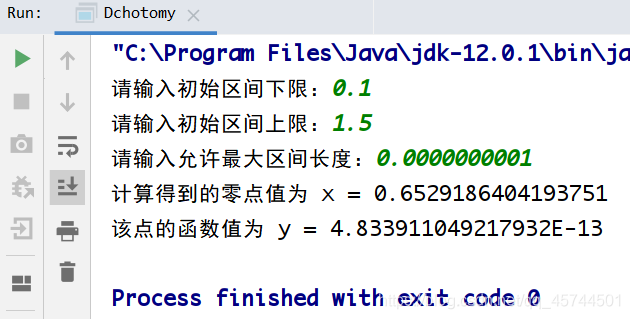
Source Codes(完整代码见github)

/**
 * @Classname Dchotomy
 * @Description TODO
 * @Date 2020/4/24 16:12
 * @Created by Jason
 */
public class Dchotomy {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.print("请输入初始区间下限：");
        double a = scanner.nextDouble();
        System.out.print("请输入初始区间上限：");
        double b = scanner.nextDouble();
        System.out.print("请输入允许最大区间长度：");
        double e = scanner.nextDouble();
        List<Double> result = getEstimates(a,b,e);
        System.out.println("计算得到的零点值为 x = " + result.get(0));
        System.out.println("该点的函数值为 y = " + result.get(1));
    }

    private static List<Double> getEstimates(double a,double b,double e) {
        if(b <= a){
            throw  new RuntimeException("上限<=下限，计算失败...");
        }
        List<Double> reslut = new ArrayList<>();
        double y0,x,y;
        x = y = 0;
        y0 = f(a);
        int i = 0;
        while ( (b - a) >= e ) {
            i++;
            x = (a + b)/2;
            y = f(x);
            if(y*y0 > 0){
                a = x;
            }else {
                b = x;
            }
            if(i == 10000){
                System.out.println("运行超时...检查while循环结构");
                break;
            }
        }
        reslut.add(x);
        reslut.add(y);
        return reslut;
    }

    private static double f(double a) {
        return Math.log(a) + a*a;
    }
}

牛顿(Newton)迭代法

简介

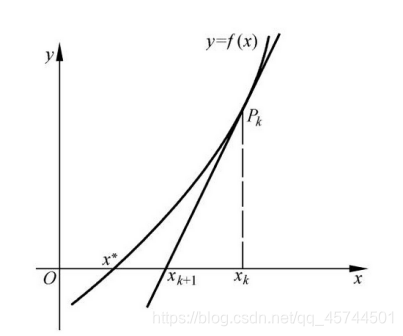
牛顿公式

$x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)}$

迭代公式

$\varphi(x)=x-\frac{f(x)}{f'(x)}$
该方法是一个很有效的求根方法，利用给出的初始值条件，得到该函数曲线上该点的切线，通过切线与x轴的交点得到下一个近似零点，以此循环迭代求解，直到区间的长度满足要求。它的收敛速度很快，一般我们使用二分法来初步缩短待求区间长度，然后使用牛顿法进行快速收敛。

算法描述

变量说明

$x_0$:初始近似值
$e$:最大允许区间长度
$N_0$：迭代次数

程序运行结果截图

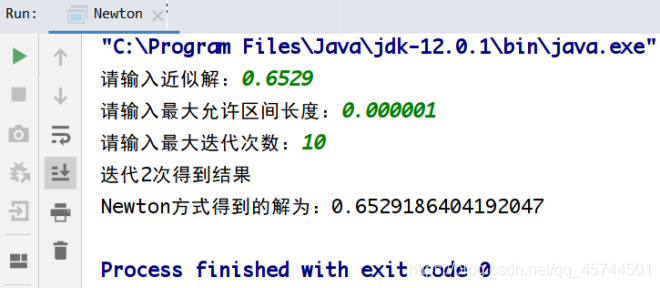
Source Codes(完整代码见github)

/**
 * @Classname Newton
 * @Description TODO
 * @Date 2020/4/24 17:35
 * @Created by Jason
 */
public class Newton {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.print("请输入近似解：");
        double x = scanner.nextDouble();
        System.out.print("请输入最大允许区间长度：");
        double e = scanner.nextDouble();
        System.out.print("请输入最大迭代次数：");
        int N = scanner.nextInt();
        scanner.close();
        double res = getEistimate(x,e,N);
        System.out.println("Newton方式得到的解为：" + res);
    }

    private static double getEistimate(double x,double e,int N) {
        double result,x1;
        for (int k = 1; true ; k++ ) {
            if(f(x) == 0){
                throw new RuntimeException("出现奇异情况....");
            }
            x1 = x - F(x)/f(x);
            if(Math.abs(x1 - x) < e ){
                System.out.println("迭代" + k + "次得到结果");
                return x1;
            }
            if(k == N){
                throw new RuntimeException("迭代失败，已达最大迭代次数N....");
            }
            x = x1;
        }
    }

    private static double F(double x) {
        return Math.log(x) + x*x;
    }

    private static double f(double x) {
        return 2*x + 1/x;
    }

}

快速弦截法

简介

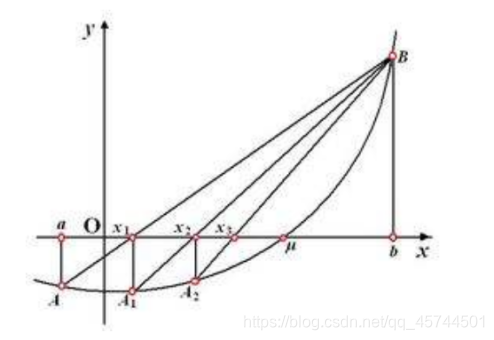
这种方法实际上和牛顿法的思想是极其相似的，不过牛顿法有一个缺点就是对于简单的函数我们可以求出它的导数，但对于复杂的函数，它的导数很复杂，或有些函数的导数无法用初等函数的形式表示，那么牛顿法就会显得心有力而力不足了。弦截法就进行了对导数进行了“曲线救国”，用差商：
$\frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}$
来代替牛顿公式中的导数 $f'(x_k)$,得到下列迭代公式:
$x_{k+1}=x_k-\frac{f(x_k)}{f(x_k)-f(x_{k-1})}(x_k-x_{k-1})$
在保证了收敛速度的前提下，巧妙的避免了求解导数的麻烦，不过在给初始条件时需要给出两个值，才能开始计算。

算法描述

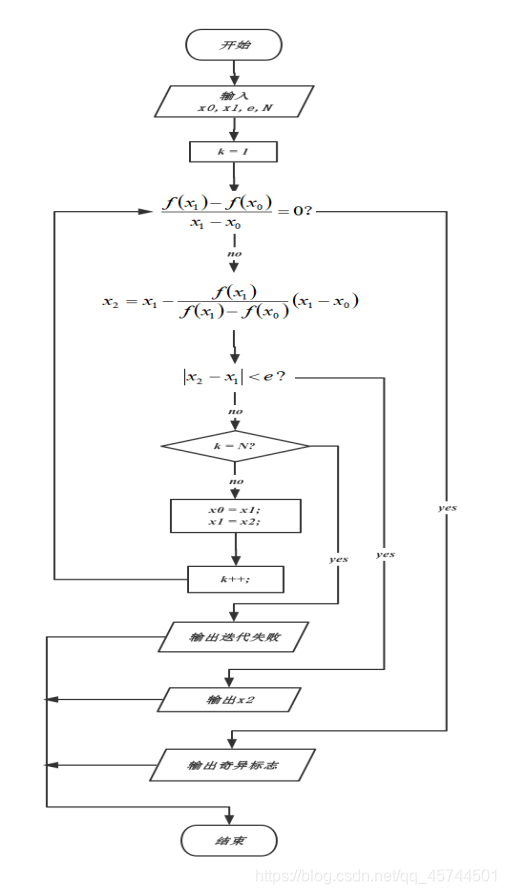
程序运行结果截图

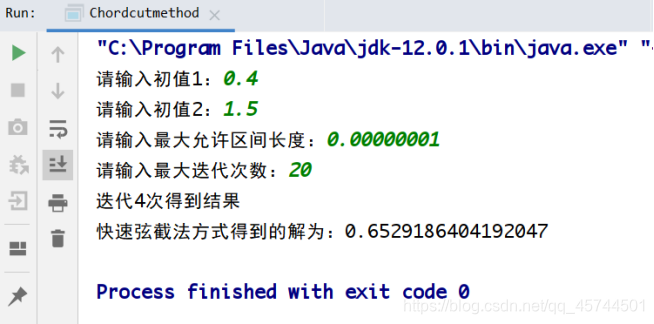
Source Codes(完整代码见github)

/**
 * @Classname Chordcutmethod
 * @Description TODO
 * @Date 2020/4/24 18:51
 * @Created by Jason
 */
public class Chordcutmethod {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        System.out.print("请输入初值1：");
        double x0 = scanner.nextDouble();
        System.out.print("请输入初值2：");
        double x1 = scanner.nextDouble();
        System.out.print("请输入最大允许区间长度：");
        double e = scanner.nextDouble();
        System.out.print("请输入最大迭代次数：");
        int N = scanner.nextInt();
        scanner.close();
        double res = getEistimate(x0,x1,e,N);
        System.out.println("快速弦截法方式得到的解为：" + res);
    }

    private static double getEistimate(double x0,double x1,double e,int N) {
        double x2;
        for (int k = 0; true ; k++ ) {
            if(f(x0,x1) == 0){
                throw new RuntimeException("出现奇异情况....");
            }
            x2 = x1 - F(x1)/f(x0,x1);
            if(Math.abs(x2 - x1) < e){
                System.out.println("迭代" + k + "次得到结果");
                return x2;
            }
            if(k == N){
                throw new RuntimeException("迭代失败，已达最大迭代次数N....");
            }
            x0 = x1;
            x1 = x2;
        }
    }

    private static double f(double x0, double x1) {
        return (F(x1) - F(x0))/(x1 - x0);
    }

    private static double F(double x) {
        return Math.log(x) + x*x;
    }

}

小结

方程求根是一个很现实的问题，这节实验通过对二分法求解、牛顿法求解和快速弦截法分别对 $y=f\left(x\right)=x^2+lnx,(x>0).$:进行了细致研究，得到比较满意的结果。