#include<iostream>
#include<math.h>
using namespace std;
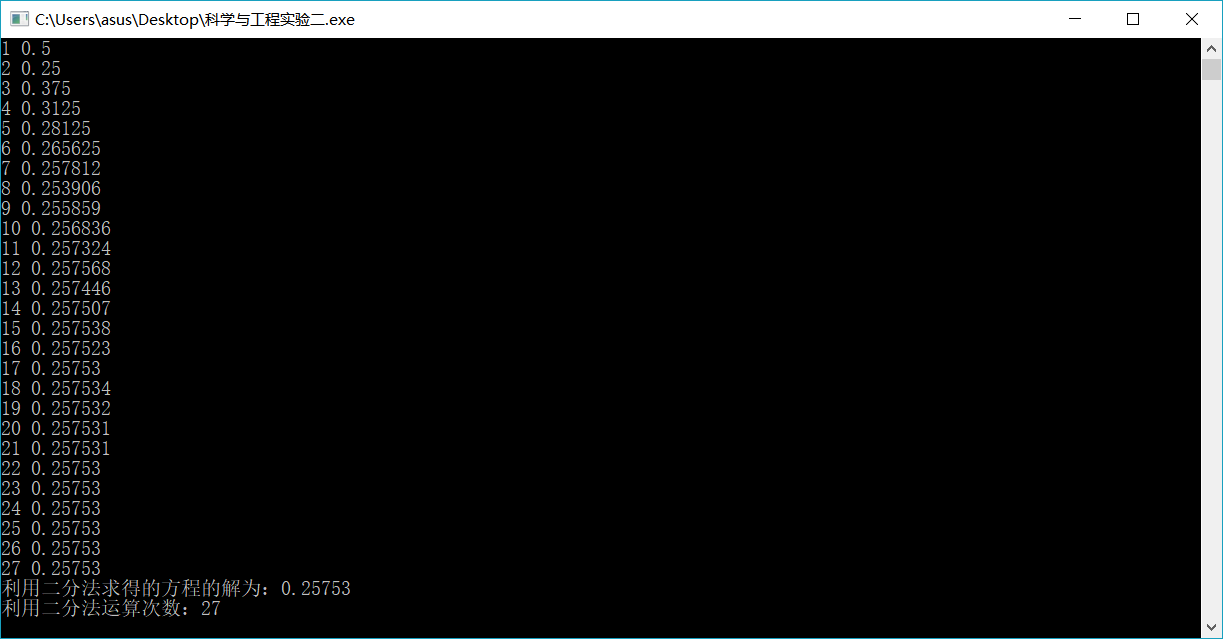
/*int main() //二分法 解为0.25753 运算次数27
{
double a=0,b=1;
double x;
double l;
int k=0;
while(fabs(a-b)>=0.00000001)
{
x=(a+b)/2;
k++;
cout<<k<<" "<<x<<endl;
if((x*x-3*x+2-exp(x))<0)
b=x;
else if((x*x-3*x+2-exp(x))>0)
a=x;
else
{
l=x;
break;
}
}
l=x;
cout<<"利用二分法求得的方程的解为:"<<l<<endl;
cout<<"利用二分法运算次数:"<<k<<endl;
return 0;
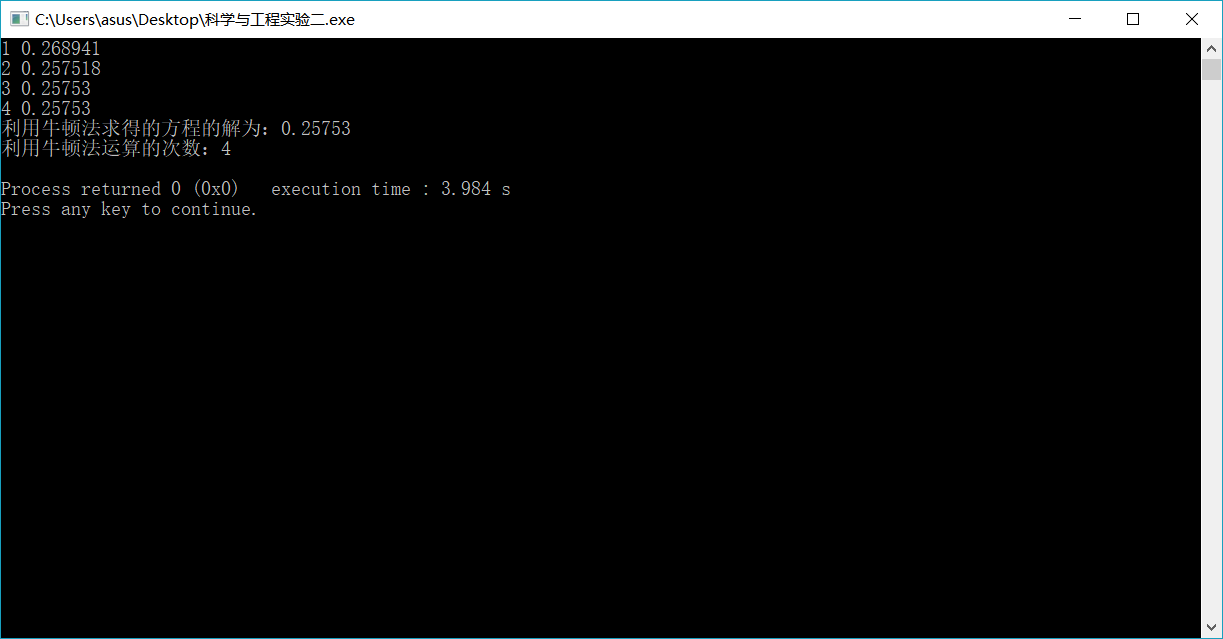
/*int main() //牛顿法 解为0.25753 运算次数4
{
double a=1;
double b=a-(a*a-3*a+2-exp(a))/(2*a-3-exp(a));
int tag=0;
int k=1;
cout<<k<<" "<<b<<endl;
while (fabs(a-b)>=0.00000001)
{
if(tag==0)
{
a=b-(b*b-3*b+2-exp(b))/(2*b-3-exp(b));
tag=1;
k++;
cout<<k<<" "<<a<<endl;
}
else
{
b=a-(a*a-3*a+2-exp(a))/(2*a-3-exp(a));
tag=0;
k++;
cout<<k<<" "<<b<<endl;
}
}
if(tag==1)
cout<<"利用牛顿法求得的方程的解为:"<<a<<endl;
else
cout<<"利用牛顿法求得的方程的解为:"<<b<<endl;
cout<<"利用牛顿法运算的次数:"<<k<<endl;
return 0;
/*int main() //牛顿下山法 解为0.25753 运算次数4
{
double i=1;
double a=1;
double b=a-i*(a*a-3*a+2-exp(a))/(2*a-3-exp(a));
int k=1;
cout<<k<<" "<<b<<endl;
if(fabs(b)>=fabs(a))
i=i/2;
int tag=0;
while (fabs(a-b)>=0.00000001)
{
if(tag==0)
{
a=b-i*(b*b-3*b+2-exp(b))/(2*b-3-exp(b));
tag=1;
if(fabs(a)>=fabs(b))
i=i/2;
k++;
cout<<k<<" "<<a<<endl;
}
else
{
b=a-i*(a*a-3*a+2-exp(a))/(2*a-3-exp(a));
tag=0;
if(fabs(b)>=fabs(a))
i=i/2;
k++;
cout<<k<<" "<<b<<endl;
}
}
if(tag==1)
cout<<"利用牛顿下山法求得的方程的解为:"<<a<<endl;
else
cout<<"利用牛顿下山法求得的方程的解为:"<<b<<endl;
cout<<"利用牛顿下山法运算的次数:"<<k<<endl;
return 0;
}*/

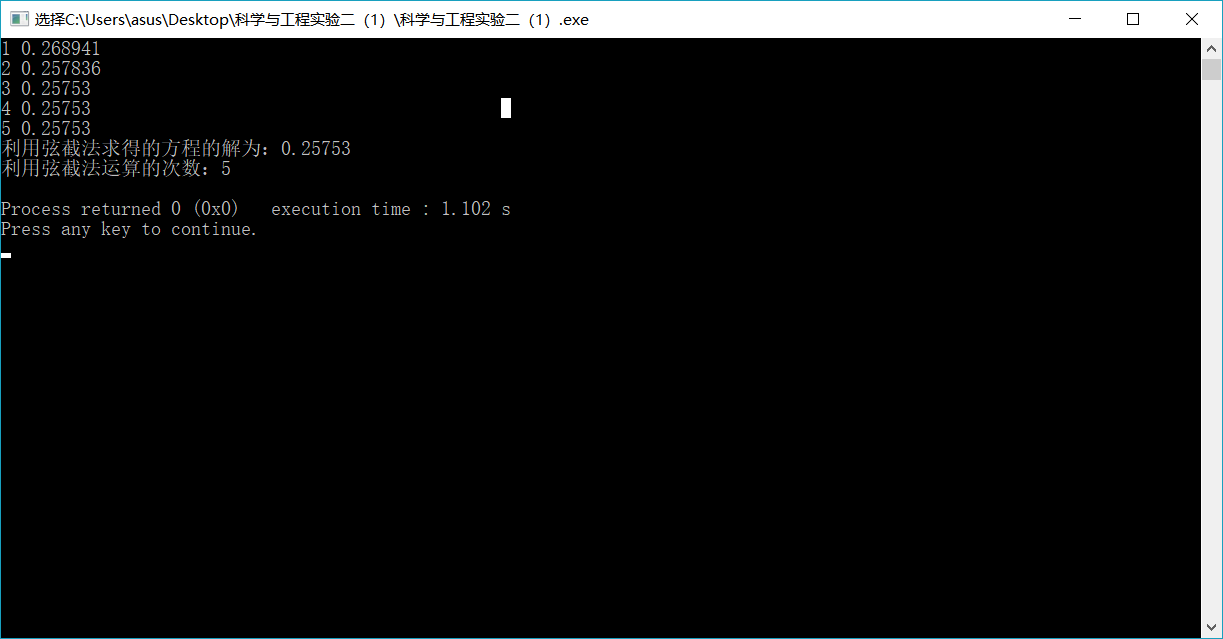
/*int main() //弦截法 解为0.25753 运算次数5
{
double a=0,b=1;
double c;
c=a-((a*a-3*a+2-exp(a))/((a*a-3*a+2-exp(a))-(b*b-3*b+2-exp(b))))*(a-b);
int k=1;
cout<<k<<" "<<c<<endl;
int tag=1;//c a b
while((tag==1&&fabs(c-a)>=0.00000001)||(tag==2&&fabs(b-c)>=0.00000001)||(tag==3&&fabs(a-b)>=0.00000001))
{
if(tag==1)
{
b=c-((c*c-3*c+2-exp(c))/((c*c-3*c+2-exp(c))-(a*a-3*a+2-exp(a))))*(c-a);
tag=2;//b c a
k++;
cout<<k<<" "<<b<<endl;
}
else if(tag==2)
{
a=b-((b*b-3*b+2-exp(b))/((b*b-3*b+2-exp(b))-(c*c-3*c+2-exp(c))))*(b-c);
tag=3;//a b c
k++;
cout<<k<<" "<<a<<endl;
}
else
{
c=a-((a*a-3*a+2-exp(a))/((a*a-3*a+2-exp(a))-(b*b-3*b+2-exp(b))))*(a-b);
tag=1;//c b a
k++;
cout<<k<<" "<<c<<endl;
}
}
if(tag==1)
cout<<"利用弦截法求得的方程的解为:"<<c<<endl;
else if(tag==2)
cout<<"利用弦截法求得的方程的解为:"<<b<<endl;
else
cout<<"利用弦截法求得的方程的解为:"<<a<<endl;
cout<<"利用弦截法运算的次数:"<<k<<endl;
return 0;
#include<math.h>
using namespace std;
/*int main() //二分法 解为0.25753 运算次数27
{
double a=0,b=1;
double x;
double l;
int k=0;
while(fabs(a-b)>=0.00000001)
{
x=(a+b)/2;
k++;
cout<<k<<" "<<x<<endl;
if((x*x-3*x+2-exp(x))<0)
b=x;
else if((x*x-3*x+2-exp(x))>0)
a=x;
else
{
l=x;
break;
}
}
l=x;
cout<<"利用二分法求得的方程的解为:"<<l<<endl;
cout<<"利用二分法运算次数:"<<k<<endl;
return 0;
}*/
/*int main() //牛顿法 解为0.25753 运算次数4
{
double a=1;
double b=a-(a*a-3*a+2-exp(a))/(2*a-3-exp(a));
int tag=0;
int k=1;
cout<<k<<" "<<b<<endl;
while (fabs(a-b)>=0.00000001)
{
if(tag==0)
{
a=b-(b*b-3*b+2-exp(b))/(2*b-3-exp(b));
tag=1;
k++;
cout<<k<<" "<<a<<endl;
}
else
{
b=a-(a*a-3*a+2-exp(a))/(2*a-3-exp(a));
tag=0;
k++;
cout<<k<<" "<<b<<endl;
}
}
if(tag==1)
cout<<"利用牛顿法求得的方程的解为:"<<a<<endl;
else
cout<<"利用牛顿法求得的方程的解为:"<<b<<endl;
cout<<"利用牛顿法运算的次数:"<<k<<endl;
return 0;
}*/
/*int main() //牛顿下山法 解为0.25753 运算次数4
{
double i=1;
double a=1;
double b=a-i*(a*a-3*a+2-exp(a))/(2*a-3-exp(a));
int k=1;
cout<<k<<" "<<b<<endl;
if(fabs(b)>=fabs(a))
i=i/2;
int tag=0;
while (fabs(a-b)>=0.00000001)
{
if(tag==0)
{
a=b-i*(b*b-3*b+2-exp(b))/(2*b-3-exp(b));
tag=1;
if(fabs(a)>=fabs(b))
i=i/2;
k++;
cout<<k<<" "<<a<<endl;
}
else
{
b=a-i*(a*a-3*a+2-exp(a))/(2*a-3-exp(a));
tag=0;
if(fabs(b)>=fabs(a))
i=i/2;
k++;
cout<<k<<" "<<b<<endl;
}
}
if(tag==1)
cout<<"利用牛顿下山法求得的方程的解为:"<<a<<endl;
else
cout<<"利用牛顿下山法求得的方程的解为:"<<b<<endl;
cout<<"利用牛顿下山法运算的次数:"<<k<<endl;
return 0;
}*/

/*int main() //弦截法 解为0.25753 运算次数5
{
double a=0,b=1;
double c;
c=a-((a*a-3*a+2-exp(a))/((a*a-3*a+2-exp(a))-(b*b-3*b+2-exp(b))))*(a-b);
int k=1;
cout<<k<<" "<<c<<endl;
int tag=1;//c a b
while((tag==1&&fabs(c-a)>=0.00000001)||(tag==2&&fabs(b-c)>=0.00000001)||(tag==3&&fabs(a-b)>=0.00000001))
{
if(tag==1)
{
b=c-((c*c-3*c+2-exp(c))/((c*c-3*c+2-exp(c))-(a*a-3*a+2-exp(a))))*(c-a);
tag=2;//b c a
k++;
cout<<k<<" "<<b<<endl;
}
else if(tag==2)
{
a=b-((b*b-3*b+2-exp(b))/((b*b-3*b+2-exp(b))-(c*c-3*c+2-exp(c))))*(b-c);
tag=3;//a b c
k++;
cout<<k<<" "<<a<<endl;
}
else
{
c=a-((a*a-3*a+2-exp(a))/((a*a-3*a+2-exp(a))-(b*b-3*b+2-exp(b))))*(a-b);
tag=1;//c b a
k++;
cout<<k<<" "<<c<<endl;
}
}
if(tag==1)
cout<<"利用弦截法求得的方程的解为:"<<c<<endl;
else if(tag==2)
cout<<"利用弦截法求得的方程的解为:"<<b<<endl;
else
cout<<"利用弦截法求得的方程的解为:"<<a<<endl;
cout<<"利用弦截法运算的次数:"<<k<<endl;
return 0;
}*/