马尔科夫链蒙特卡洛算法（python）

参考文献：

• [1] 从马尔可夫链到蒙特卡洛-Metropolis方法（Python）
• [2] 蒙特卡洛（youtube视频）
• [3] mcint

本文参考了如上的文献、视频，以下图片部分来自于参考文献截图

1 蒙特卡洛算法

1.1 基本思想

蒙特卡洛方法是在计算总体均值、总体方差、总体分位数等数字特征时，有时由于计算复杂性难以计算，于是采用样均值、样本方差、样本分位数来估计相应总体数字特征的一种方法。总的来说就是采用样本估计总体的一种统计方法。

1.2 蒙特卡洛积分

1.2.1 求 $\pi$

随机在正方形上撒点，落在圆中的概率为圆的面积除以正方形面积，即为 $p=\pi/4$,所以 $\pi=4\times p$

• 使用蒙特卡洛计算的code

import numpy as np

samples = 1000
x = np.random.uniform(-1,1,samples)
y = np.random.uniform(-1,1,samples)
counts = len(np.where(x**2+y**2<1)[0])
p = counts/samples
pi_out = 4*p
print(pi_out)

（注意我没有采用for循环，因为for太慢了，我直接使用数组来计算会极大提高速度）

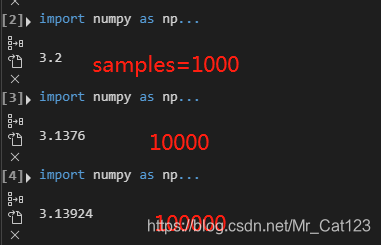
样本越大误差越小，误差跟 $1/\sqrt{samples}$成正比

1.2.2 求积分

1.2.2.1 一维积分

看一下步骤：

上面实际上就是将积分变为求和，我们跟梯形面积法求积分对比一下，

梯形面积法求积分如下
$\int_a^bf(x)dx\simeq\sum_{i=1}^nf(x_i)\Delta x_i$
这里 $\Delta x_i$表示步长, 不难发现，蒙特卡洛撒点积分的方法相当于 $(b-a)/n=\Delta x_i$,表示每个步长是一样的，即对应的梯形中的高是一样的.(将积分区间等分)。但是值得注意的是，这里的 $x_i$(即第i个x的值)是随机撒点的，所以会出现比较大的误差（比如撒的点集中在0附近，那么值就会偏小；集中在1附近，值就会偏大），而我们常规的小面积代替积分的方法中， $x_i$是递增的，因此不会存在点集中在某个值附近的情况，这使得我们的误差会比蒙特卡洛撒点的方法小。不过，如果撒的点很多，也就是 $n\sim\infty$,那么从大数定理出发，得到的值是跟真值一样的。

1） 先计算一个简单的积分
$S=\int_0^1xdx$
我们可以使用蒙特卡洛数值撒点（随机撒点），那么上面变为求和
$S\simeq\sum_{x_i =0}^1x_i\Delta x_i=(1-0)/n\times \sum_{i=0}^nx_i$
其中n是样本数，
以下使用三种方法实现积分。顺序分别对应：蒙特卡洛法，梯形面积法和调用函数（调用的正是蒙特卡洛程序）第三个跟第一个程序是一样的。
python code实现如下：

import numpy as np
import mcint
#蒙特卡洛撒点
samples = 1000
x = np.random.uniform(0,1,samples)  #x 是0，1之间随机撒点
S = (1-0)/samples*np.sum(x)
print(S)
#梯形面积积分
x2 = np.linspace(0,1,num=samples)  # x2是递增的
delta_x = 1./samples
S2 = delta_x*np.sum(x2)
print(S2)

#mcint
def integrand(x):
    return x

def sampler():
    while True:
        x = np.random.random()   #生成（0，1）的数
        yield x

result,error = mcint.integrate(integrand,sampler(),measure=1.0,n=samples)
print(result,error)

第一个方法跟解析解的真实值0.5很接近，而第二个方法完全相等，这是因为y=x本来就是一条斜线，构成一个梯形，所以samples=2也会使得第二个方法=0.5。因此对于一维积分而言，后者比蒙特卡洛随机撒点更好。
对mcint这个函数做一个简单解释，具体可以看上面的链接。measure是你要积分的范围，n是样本数（默认=100），integrand是被积函数，sampler()是样本生成器（因为使用的是yield)
关于误差跟样本数之间的关系，如下（参考从马尔可夫链到蒙特卡洛-Metropolis方法（Python））：

2）计算积分
$S=\int_{-2}^4x^2dx$

import numpy as np
import mcint

#蒙特卡洛
samples = 1000
x = np.random.uniform(-2,4,samples)
S = (4+2)/samples*np.sum(x**2)
print(S)

#梯形面积法
x2 = np.linspace(-2,4,num=samples)
delta_x = (4+2)/samples
S2 = delta_x*np.sum(x2**2)
print(S2)

#mcint
def integrand(x):
    return x**2

def sampler():
    while True:
        x = np.random.uniform(-2,4)   #生成（-2，4）的数
        yield x

result,error = mcint.integrate(integrand,sampler(),measure=6.0,n=samples)
print(result,error)

生成三次，可以看到，梯形面积法最接近真实值（24）最接近，误差最小（因为它的误差 $\sim 1/n^2,而蒙特卡洛法\sim 1/\sqrt{n}$)。原因也说过了，梯形面积法中 $x_i$是递增的，因此是均匀的，只有当蒙特卡洛撒点是足够多的时候才会出现各处分布均匀的情况。

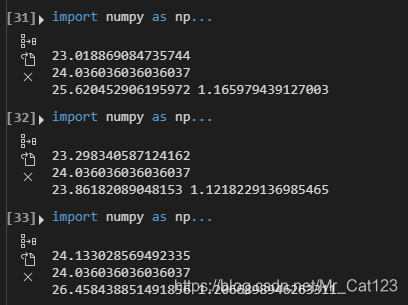
调用函数mcint有一个要求，就是你必须知道积分区间，即上面的measure。

1.2.2.2 高维积分

具体步骤如下

上面可以看到，要使用蒙特卡洛求多维积分，首先要知道多维积分区间构成的体积 $V$(二维就是面积），也就是直接令被积函数为1，然后求积分。有时候这个体积跟原被积函数一样难求，那么就不能用蒙特卡洛了。所以这种情况针对的是 $V$很好求的情况，比如正方体，扇形，柱体等等。
1）计算积分
$\int_0^1\int_0^{\sqrt{1-y^2}}(x^2+y^2)dxdy$
1.1）使用蒙特卡洛方法：
这个积分区间不难看出是1/4圆的面积（x正的那部分）,所以实际上我们知道 $V=\pi/4$.也就是
$\int_0^1\int_0^{\sqrt{1-y^2}}dxdy=\pi/4$
当然，不知道= $\pi/4$也没事，可以很快积分出来。首先令被积函数为1，那么
$V=\int_0^1\int_0^{\sqrt{1-y^2}}dxdy=\int_0^1\sqrt{1-y^2}dy$
（实际上这里已经很容易看出来是函数 $\sqrt{1-y^2}与y轴的构成的面积，即1/4圆。）$上面的积分使用一个技巧，（很多链接可以找到这个积分方法，如求不定积分）。
由于根号下要求为正，而 $1-y^2$又小于等于1，所以 $1-y^2$要求在[0,1]区间中，这让我们想起了三角函数，所以令 $y=\sin\theta,\theta\in(-\pi/2,\pi/2)$,所以
$V=\int_0^1\cos^2\theta d\theta=...=y\sqrt{1-y^2}\big|_0^1+1/2\arcsin(y)\big|_0^1\simeq0.7854$
上面我直接给出了积分的结果。
使用蒙特卡洛积分法的code如下：

import numpy as np

#蒙特卡洛撒点
samples = 100
y = np.random.uniform(0,1,samples)
x = np.random.uniform(0,1-y**2)
V = 0.7854
S = V/samples*np.sum(x**2+y**2)
print(S)

1.2）使用梯形求和法：

ans = 0
step_x = 0.01
step_y = 0.01
for y in np.arange(0,1,step_y):
    for x in np.arange(0,y,step_x):
        ans = ans + (x**2+y**2)*step_x*step_y
print(ans)

我上面使用两层for是为了看得更加明白，实际上建议使用数组，计算更快。
1.3）调用mcint积分
再次说明，这跟蒙特卡洛是一样的

import numpy as np
import mcint

samples = 10000
def integrand(x):
    return (x[0]**2 + x[1]**2)

def sampler():
    while True:
        y = np.random.random()
        x = np.random.random()
        if x**2+y**2 <= 1:
            yield (x,y)

result, error = mcint.integrate(integrand, sampler(), measure=np.pi/4,n=samples)
print(result,error)

1.3 蒙特卡洛期望估计

如一开始所述，蒙特卡洛的最大运用并不是在积分上，而是在使用样本估计总体的数字特征上，比如求期望。这在机器学习等方面有很大应用。

上面的步骤具体如下：

• 1， 如果样本服从某个概率分布 $p(x)$，那么通过概率分布 $p(x)$来撒点，比如服从均匀分布，则用rand.uniform()撒点（得到的点有相同的概率），服从高斯分布则用高斯分布器来撒点。
• 2, 求这些点的期望，这个估计的期望用来代替真实的期望值。