Python中的贝叶斯推断和马尔科夫链蒙特卡洛抽样调查
介绍使用贝叶斯推断和MCMC抽样方法,通过在Python中实现的一个深入的抛硬币的例子来预测未知参数的分布。

简介
本文将一个基本的抛硬币的例子扩展到一个更大的范围,在这个范围内,我们可以检查贝叶斯推理和马尔科夫链蒙特卡洛抽样的使用和力量,以预测未知的值。有许多有用的软件包可以采用MCMC方法,但在这里我们将在Python中从头开始建立我们自己的MCMC,目的是了解这个过程的核心。
什么是贝叶斯推理?
贝叶斯推断是一种方法,其中我们使用贝叶斯定理来更新我们对一个概率或参数的理解,因为我们收集了更多的数据和证据。
什么是马尔科夫链蒙特卡洛采样?
MCMC方法(它通常被称为)是一种用于从概率分布中取样的算法。这类算法采用随机抽样的方式来实现数字结果,随着样本数量的增加,数字结果会收敛于真相。有许多不同的算法可以用来创建这种类型的抽样链--在这个具体的例子中,我们将利用的算法叫做Metropolis-Hastings算法。MH的实现允许我们从一个未知的分布中抽取样本,前提是我们知道一个与我们想要抽取的分布的概率密度成正比的函数。不需要知道确切的概率密度,只需要知道它的比例关系,这使得MCMC-MH特别有用。我们将在本例后面描述该算法的详细步骤。
硬币工厂问题
这个例子将对翻转硬币的结果的概率进行建模,但在一个扩展的背景下。想象一下,一个全新的硬币工厂刚刚建成,用于生产一种新的硬币,他们要求你确定工厂生产的硬币的一个参数--在翻转时硬币落在头/尾的概率。我们把这称为硬币的 "偏向"。
每枚硬币都会有自己的偏向,但考虑到它们是在相同的过程中生产的,而且只有微小的差异,我们希望工厂生产的硬币不是随机的,而是围绕着 "工厂偏向"。我们将使用来自特定硬币和工厂偏差的信息来创建一个概率分布,以确定一枚硬币最可能以何种偏差生产。用贝叶斯的术语来说,我们将使用似然(硬币数据)和先验(工厂偏差)来产生硬币偏差的后验分布。

于是,工厂开工了,生产了第一枚硬币。鉴于这是一种新的硬币和铸币厂,我们对它翻转时的行为方式并不了解(假装我们不知道硬币一般是如何工作的,我们正试图预测一个 "未知 "参数)。因此,我们用这第一枚硬币做实验,翻转100次,并记录它落在头顶的次数 - 57次。我们将用更多的硬币进行实验,以更新我们对工厂偏差的理解,但首先,让我们只分析第一枚硬币。
贝叶斯背景下的问题
在我们走得太远之前,我们需要在贝叶斯定理的背景下定义这个问题。等式的左边被称为后验;一般来说,它是指在某些证据(E)的情况下,一个假设(H)的概率。在右边的分子中,我们有我们的可能性(鉴于我们的假设是真的,看到证据的概率),乘以先验(假设的概率)。左边的分母是边际可能性或证据;这是观察到证据的概率。幸运的是,我们不需要使用边际似然来对后验进行取样。
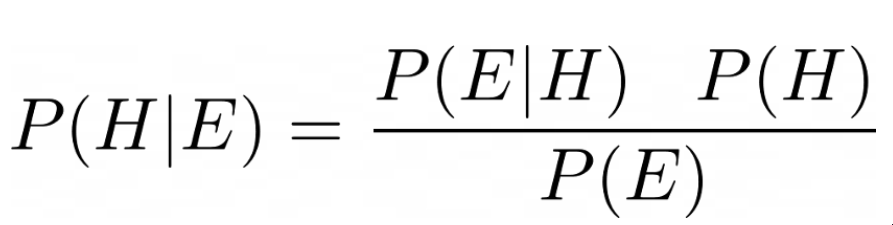
贝叶斯定理
在大多数实际应用中,直接计算后验分布是不可能的,这就是为什么我们采用MCMC这样的数字抽样技术。
后验 那么,对于我们的硬币厂,我们感兴趣的后验概率是什么呢?它是指在我们的数据下,工厂生产出有偏差的硬币的概率P,即头数为x的概率--P(p|x)。该定理的其余部分可以写成如下。
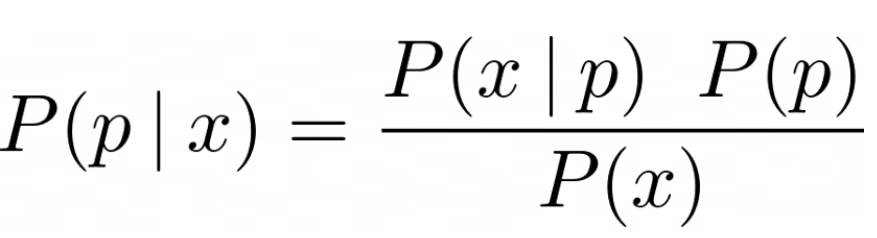
贝叶斯法则在我们的硬币工厂中的应用
在这里必须记住,我们是在预测硬币有一定概率的头的后验概率分布(P(p|x)),或者说偏向(p),这是两件不同的事情。工厂Bais是指一枚硬币产生一定偏差的概率分布;这就是P(p),即先验。
可能性 - 二项分布
这里的似然函数是指在硬币有偏差p的情况下,观察到人头的概率,x。对于一个有偏差的硬币,在n次抛掷中观察到x个头的概率可以写成。
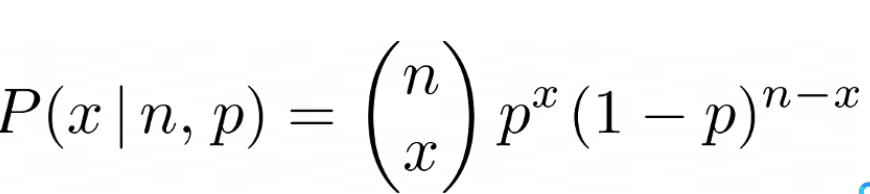
二项分布 - 图片由作者提供
值得注意的是,我们目前并不知道某个硬币的p值。这个值是我们的MCMC将随机取样的一个值。在用一个随机值初始化p后,通过多次采样,模型将向p的真实值收敛。
让我们开始用Python对这个例子进行编码。我们需要定义第一个硬币实验的观察数据,以及一个似然函数,该函数给出了我们数据的二项分布的概率。Scipy.stats是一个很好的Python库,可以很容易地定义二项分布,我在这个例子中就是用它。
# Define the data
x = 57
n = 100
# Define the Likelihood P(x|p) - binomial distribution
def likelihood(p):
return stats.binom.pmf(x, n, p)
先验
接下来,我们需要定义我们的先验函数,P(p)。P的值只能存在于0和1之间,0代表一个永远不会有头的硬币,1代表一个永远有头的硬币。请记住,工厂只生产了一枚硬币,所以我们没有任何关于预期p的先验概率的信息(假装我们不知道硬币的工作原理)。
在这个问题的背景下,由于只生产了一枚硬币,我们还不知道工厂的偏差可能是什么。正因为如此,我们将使用所谓的统一先验。在贝叶斯推理的背景下,这意味着我们对p是0和1之间任何数值的概率赋予同等的权重。
我们可以用Scipy和均匀分布PDF轻松做到这一点。这个默认分布只存在于0到1之间,正如我们需要的那样。
# Define Prior Function - Uniform Distribution
def prior(p):
return stats.uniform.pdf(p)
现在我们已经定义了我们的似然和先验,我们可以继续理解和编码马尔科夫链。
Metropolis-Hastings MCMC 如上所述,这些方法是从一个连续的随机变量中抽取样本--在我们的例子中为p。我们将使用的MCMC是随机行走类型的,它随机生成样本,并根据它们对模型的适合程度保留它们或不保留。
接受率 Metropolis-Hastings算法是相当直接的,但首先,我们需要定义如何接受或拒绝新抽取的样本。每次迭代,都会提出一个介于0和1之间的新的p值,我们将这个建议值称为p′。我们只想接受和更新这个值,如果它比之前的值更好。这个接受率是我们的贝叶斯定理对提议值与先前值的比率,如下所示。
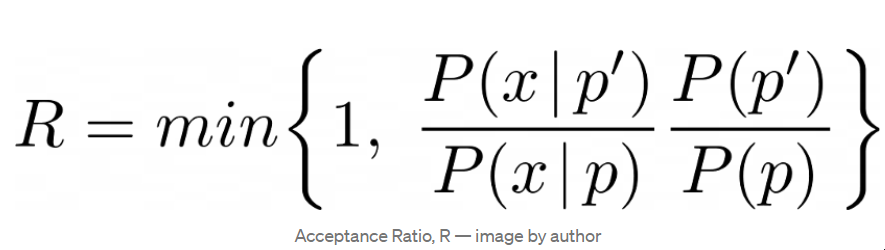
接受率,R
这里有几件事需要注意。首先,你可能已经注意到,这个接受率不包括贝叶斯定理的边际似然(证据)部分,我们也没有在上面为它定义一个函数。这是因为对于一个新的p值来说,证据并没有改变,因此在这个比率中抵消了它。
这很了不起,因为计算贝叶斯定理的边际似然部分在实践中通常非常困难或不可能。MCMC和贝叶斯推断允许我们在不需要知道边际似然的情况下对后验进行采样
第二,这里任何大于1的值都意味着提议的值更好,应该被接受。接受新值的第二部分是将R与0和1之间的另一个随机抽样进行比较,所以惯例是当R较高时直接将其设置为1。
为了简单起见,我们将写一个函数来计算这个接受率,以便在我们的采样链循环中轻松实现。
# Create function to compute acceptance ratio
# This function will accept the current and proposed values of p
def acceptance_ratio(p, p_new):
# Return R, using the functions we created before
return min(1, ((likelihood(p_new) / likelihood(p)) * (prior(p_new) / prior(p))))
让我们明确定义一下MH算法的步骤,这样就更清楚了。
采样算法 我们已经定义了似然、先验和接受概率的函数。在循环之前,我们必须做的最后一件事是用一个范围内的随机值初始化p,即0到1。
以下是我们Metropolis-Hastings算法的步骤。
在0到1之间随机提出一个新的p值,称之为p′(或p_new)。 计算接受率,R。 生成另一个介于0和1之间的均匀随机数,称为u。 如果u<R,则接受新值,并设置p=p′。否则,保留p的当前值。 记录这个样本的p的最终值。 重复步骤1到5,很多很多次。 相当简单明了。在我们编写代码之前,让我们来探讨一下MCMC中使用的其他几个常见概念。
烧录 MCMC是随机初始化的,必须向正确的值收敛,而这往往需要相当多的样本。在绘制我们的结果和后验分布时,在模型收敛之前包括这些早期样本是无效的。因此,我们实施了所谓的 "烧录",即排除那些最初的、不太准确的样本。MCMCs的烧毁通常在2000-5000个样本左右,当整个链条在10k-20k左右。
# Create empty list to store samples
results = []
# Initialzie a value of p
p = np.random.uniform(0, 1)
# Define model parameters
n_samples = 25000
burn_in = 5000
lag = 5
# Create the MCMC loop
for i in range(n_samples):
# Propose a new value of p randomly from a uniform distribution between 0 and 1
p_new = np.random.random_sample()
# Compute acceptance probability
R = acceptance_ratio(p, p_new)
# Draw random sample to compare R to
u = np.random.random_sample()
# If R is greater than u, accept the new value of p (set p = p_new)
if u < R:
p = p_new
# Record values after burn in - how often determined by lag
if i > burn_in and i%lag == 0:
results.append(p)
滞后 在MCMCs中需要考虑的另一件非常重要的事情是样本的独立性。在这里,一个新的样本往往依赖于以前的样本,因为我们有时不接受新的随机值而保留旧的。为了解决这个问题,我们实现了所谓的 "滞后"。滞后是指我们不是记录每一个样本,而是记录每一个其他的样本,或者是每第五或第十个样本。
仿真 很好,我们现在有了编写和运行我们的MCMC所需要的一切。
结果的可视化
MCMC结果通常以两种方式绘制--后验分布和跟踪图。后验可以用直方图显示,我们可以直观地检查最可能的值和方差。跟踪图显示了每个样本迭代的p值,并显示了MCMC的行为和收敛性。后验分布不应该包括烧毁样本,但是包括跟踪图的烧毁可以帮助我们检查模型的起点和收敛的程度。在下面的跟踪图中不包括烧毁样本。
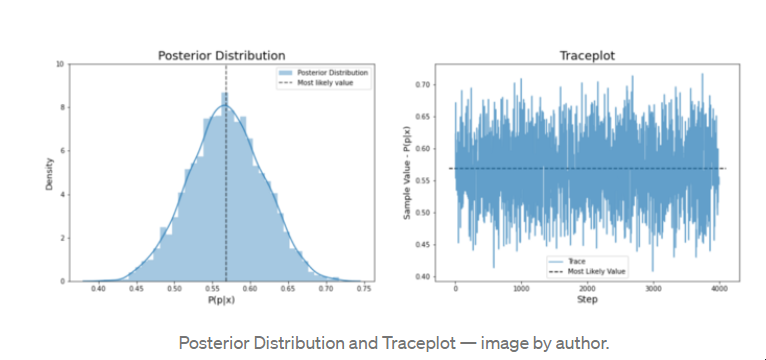
后验分布和跟踪图--图片由作者提供。 检查结果,我们可以看到,我们的后验是正态分布。我们还可以从跟踪图中看到,我们在收敛值周围进行了很好的随机采样--这很好。在提取后验值时,使用p的最后一个值与分布的其他部分不一定准确。由于这个原因,后验的值通常被当作分布的平均值。在这种情况下,我们的平均后验值是0.569。
这个值几乎就是我们对这枚硬币的数据的频率概率的预测,即57/100头。我们的MCMC之所以能预测到这一点,是因为这是第一枚硬币,而我们对它们应该如何表现并没有太多的了解。在统一先验的情况下,后验更多的是受到似然函数的影响,也就是数据的影响。
贝叶斯推断的下一步是用更多的数据来更新我们的理解,所以让我们保持工厂运转,制造更多的硬币来测试。

照片 coinFactory
更新我们的理解
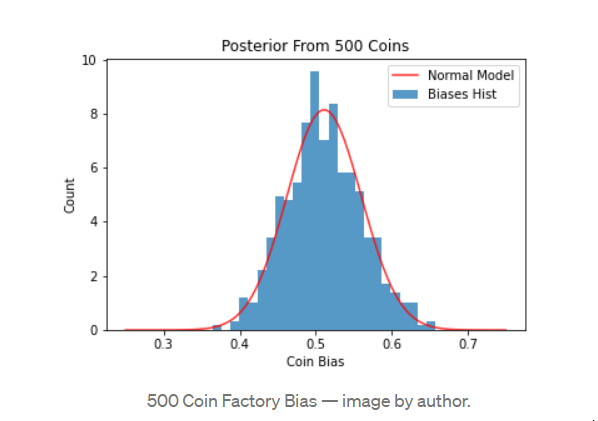
我们等了一会儿,工厂生产了500枚硬币。我们运行同样的100个翻转实验,并记录每枚硬币的后验最可能的偏向。让我们绘制一个直方图,检查产生的偏差的分布,以了解工厂的偏差。
500枚硬币的工厂偏差--图片由作者提供。 检查这个数据,我们得知平均偏差是0.511,标准偏差是0.049。这个数据看起来是正常的,所以让我们用一个具有这些参数的正态分布来建立模型--这以红色显示。
这个分布包含的信息是,对于这个工厂生产的钱币,我们预计哪些偏差更有可能出现。像这样更新我们的理解,会让我们对硬币的偏差有一个比我们之前的、无信息的、统一的先验的更准确的结果。这正是贝叶斯推断法的建立目的--我们可以简单地更新我们的先验函数来代表工厂偏见的数据。
工厂偏见先验
现在我们已经用更多的先验信息改进了我们的模型,让我们制作第501枚硬币并进行同样的实验。在这个实验中,我们在100次抛掷中得到63个头。我们必须像以前那样根据这个数据建立我们的似然函数。
# Define parameters of the Factory Bias distribution
mean = 0.511
std = 0.049
# Create prior function for this specific normal distribution
def prior(p):
return stats.norm.pdf(p, mean, std)
很好,现在让我们看看包括工厂偏差的信息对MCMC的结果有何影响,以及我们认为这枚硬币的真实偏差是什么。我运行了一个MCMC,样本数和参数与上面相同,但有更新的先验和新硬币数据。下面是第501枚硬币的后验分布和轨迹图。
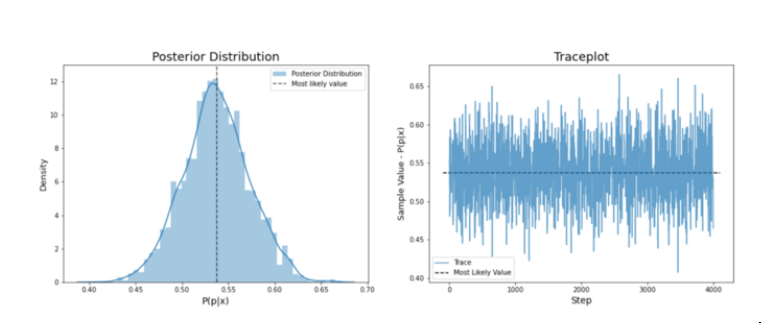
更新了先验的MCMC的后验和轨迹
尽管这枚硬币的数据表明其偏差在0.63左右,但我们的贝叶斯推理模型表明其实际值更接近于0.53。这是因为我们的知情先验函数在模型中占有权重,告诉我们即使我们观察到这枚硬币有63个头,考虑到硬币的平均偏差在0.51左右,我们预计第501枚硬币的偏差会更接近工厂偏差。即使这枚硬币的偏差正好是0.5,在100次抛掷中观察到63个头也不是完全不可能的,我们不应该认为这个数据可以代表确切的数值。
先验函数和似然函数一样,在为后验分布提供信息时拥有权重。如果我们再生产几千枚硬币,让先验分布得到更多信息,这将使它在模型中拥有更高的权重。这种用更多信息更新我们的理解以预测未知参数的想法,正是贝叶斯推理的有用之处。正是用更多、更好的数据来调整和操作这些似然和先验函数,使我们能够改进和告知我们的推理模型。
本文由 mdnice 多平台发布