题目描述:
有一个整型数组A,代表数值不同的纸牌排成一条线。玩家a和玩家b依次拿走每张纸牌,规定玩家a先拿,玩家B后拿,
但是每个玩家每次只能拿走最左或最右的纸 牌,玩家a和玩家b都绝顶聪明,他们总会采用最优策略。请返回最后获胜者的分数。
给定纸牌序列A及序列的大小n,请返回最后分数较高者得分数(相同则返回任意一个分数)。保证A中的元素均小于等于1000。且A的大小小于等于300。
测试样例:
[1,2,100,4],4
返回:
101
算法思想:
用暴力递归的方法:
f(i,j): 表示如果arr[i…j]这个排列上的纸牌被绝顶聪明的人先拿,最终能够获得什么分数。
s(i,j): 表示如果arr[i…j] 这个排列上的纸牌被绝顶聪明的人后拿,最终能获得什么分数。
在先拿的f(i,j)中:
1.如果i == j(只有一张纸牌),会被先拿纸牌的人拿走,所以返回arr[i]或arr[j];
2.如果i != j,先拿纸牌的人有两种选择,要么拿走arr[i],要么拿走arr[j];
1. 如果拿走arr[i],剩下arr[i+1,j]。对于arr[i+1,j]的纸牌,当前玩家成了后拿的人,因此他后续能获得的分数为s(i+1,j)
2. 如果拿走arr[j],那么剩下arr[i,j-1],当前玩家后续能获得的分数为s(i,j-1).
3. 作为绝顶聪明的人,必然会在两种决策中选择最优的。所以返回max{arr[i]+s[i+1,j],arr[j]+s[i][j-1]}
在后拿的s(i,j)中:
1.如果i == j,后拿纸牌的人什么也拿不到,返回0
2.如果i!=j,玩家的对手会先拿纸牌。
1. 对手要么先拿走a[i],那么排列剩下arr[i+1,j],
2. 要么先拿走arr[j],剩下arr[i,j-1]
3. 对手也是绝顶聪明的人,所以也会把最差的情况留给玩家因此返回min{f(i+1,j),f(i,j-1)}
递归版本
int first(vector<int>& arr, int i, int j)
{
if (i == j) //只有一张的情况下,先拿的就拿走
return arr[i];
return max(arr[i] + second(arr, i + 1, j), arr[j] + second(arr, i, j - 1));
}
int second(vector<int>& arr, int i, int j)
{
if (i == j)
return 0;
return min(first(arr, i + 1, j), first(arr, i, j - 1));
}
int Win1(vector<int>& arr)
{
if (arr.empty())
return 0;
return max(first(arr, 0, arr.size() - 1), second(arr, 0, arr.size() - 1));
}
DP思路:
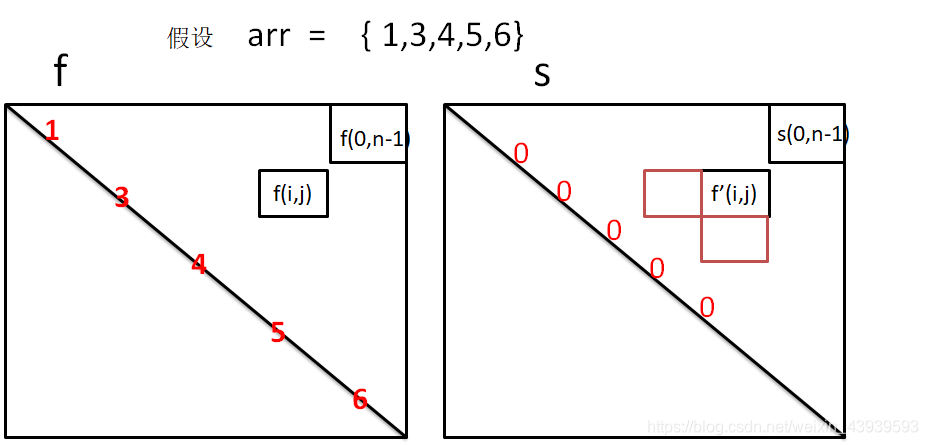
动态规划其实就是根据自己列的递归方程来确定。和题目都已经无关了。根据递归改变的参数定义我们的二维表,参数只有i和j随着改变,所以我们定义(i,j)的二维表。i是从左拿的牌,j是从右拿的牌。我们要求的答案是(0,arr.size()-1),所以两张二维表中,要求出f(0,n-1)和s(0,n-1)作为答案。又因为i<=j,所以我们要二维表的右上半部分就可以了。
初始值: f(i,i)为arr[i] ,s(i,i)为0 (都是根据递归方程得出)
不同的是,根据递归函数,f[i][j]要依赖于s[i][j]表,s[i][j]要依赖于f[i][j]表。
转移方程:
f[i][j] = max(arr[j] + s[i][j - 1],arr[i] + s[i + 1][j]);
s[i][j] = min(f[i+1][j],f[i][j-1]);
动态规划版本
int Win2(vector<int> arr)
{
int n = arr.size();
if (arr.empty())
return 0;
vector<vector<int>> f(n, vector<int>(n, 0));
vector<vector<int>> s(n, vector<int>(n, 0));
for (int i = n - 1; i >= 0 ; i--)
{
f[i][i] = i;
for (int j = i + 1; j < n; j++)
{
f[i][j] = max(arr[j] + s[i][j - 1],arr[i] + s[i + 1][j]);
s[i][j] = min(f[i+1][j],f[i][j-1]);
}
}
return max(f[0][n - 1], s[0][n - 1]);
}