斜率优化
首先,可以进行斜率优化的DP方程式一般式为$dp[i]=\max_{j=1}^{i-1}/\min_{j=1}^{i-1}\{a(i)*x(j)+b(i)*y(j)\}$
其中$a(j)$和$b(j)$都是关于$j$的函数,在$O(1)$时间内可以计算得出
将方程式进行变形
$$dp[i]=a(i)*x(j)+b(i)*y(j)$$
$$dp[i]-a(i)*x(j)=b(i)*y(j)$$
$$y(j)=-\frac{a(i)}{b(i)}x(j)+\frac{dp[i]}{b(i)}$$
我们可以称$y=-\frac{a(i)}{b(i)}x+\frac{dp[i]}{b(i)}$为i的特征直线
那么对于$i$这个决策点来说,在i之前所有决策点$j$($j<i$)可以看作一个二维平面上的点,横坐标为$x(j)$,纵坐标为$y(j)$,那么i在寻找最优决策点的过程就是用i的特征直线去截平面上的每一个点,求出截距,找到最大/最小的$dp[i]$
但如果直接去做复杂度为$O(n^{2})$
那么可以通过维护在平面上维护凸包(根据具体的斜率正负和$b(i)$的正负决定维护上凸包还是下凸包),直线在平移过程中切到凸包的第一个点就是当前i的最优决策点,那么时间复杂度均摊$O(n)$
以$-\frac{a(i)}{b(i)}>0$,$b(i)>0$,$dp$取最小值为例
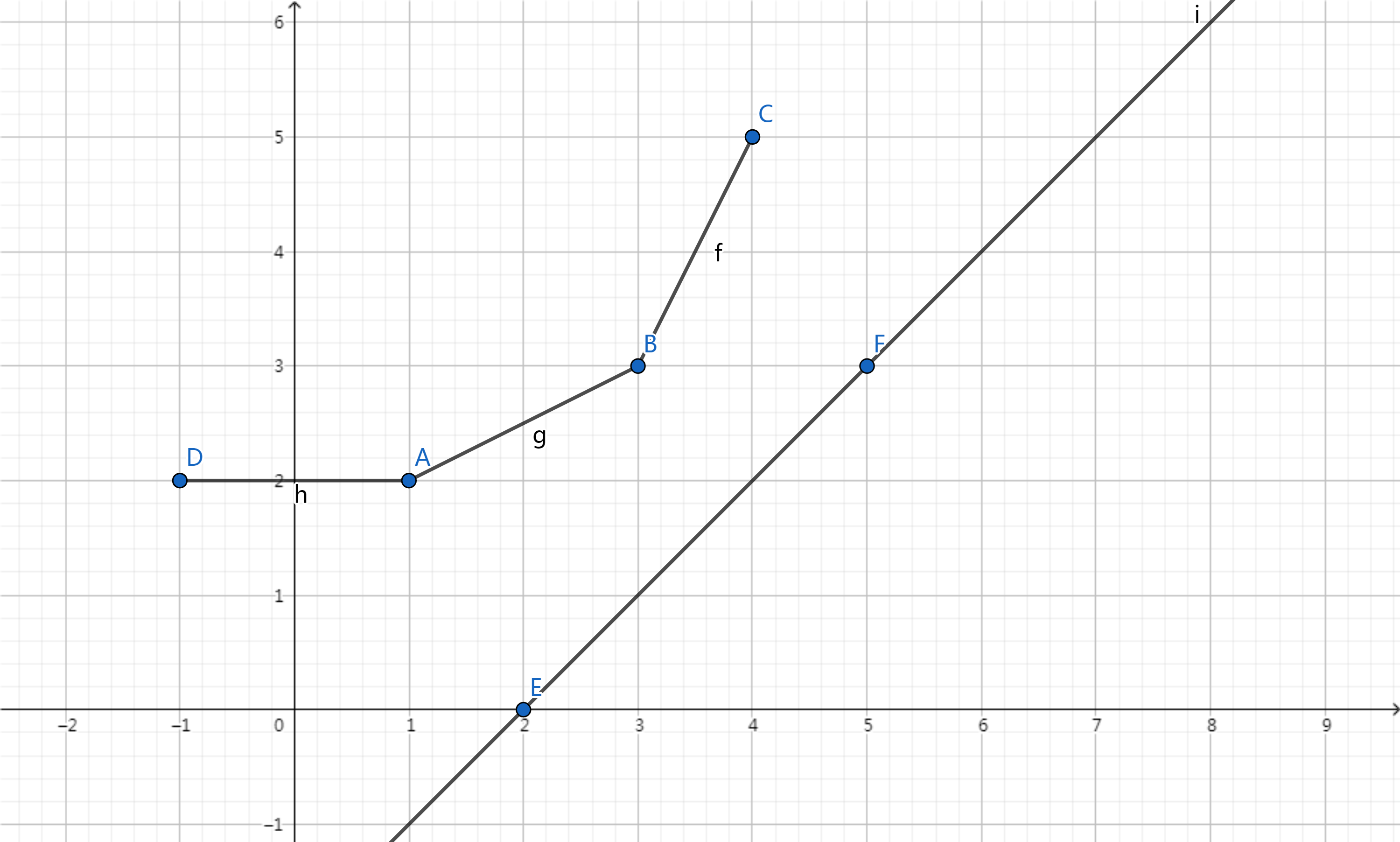
直线EF不断从截距无限小向上平移,直到截到凸包上的点
那么需要做的是维护凸包
1.若$x(i)$单调,斜率$-\frac{a(i)}{b(i)}$单调
所以在平面上的点是按顺序依次排列,去截的特征直线的斜率不断增加或减少
可以发现特征直线截到凸包上的第一个点记为$p$,那么$p$左边的点和$p$的直线的斜率$k_{1}$,$p$右边的点和$p$的直线的斜率$k_{2}$,特征直线的斜率一定介于$k_{1}$和$k_{2}$之间
那么可以利用单调队列来维护平面上的点的凸包,然后在单调队列队首不断维护当前特征直线的斜率,找到第一个大于或小于(根据凸包是上凸包还是下凸包决定)的决策点
时间复杂度$O(n)$
2.若$x(i)$单调,斜率不单调
仍然维护凸包,但此时特征直线的斜率没有规律,利用上面的结论可以二分凸包上两点的斜率,来找到第一个切到的点
时间复杂度$O(nlogn)$
3.若$x(i)$不单调,斜率不单调
对$x(i)$,斜率,时间三个维度进行cdq分治
具体见货币兑换的题解
时间复杂度$O(nlogn)$