摘要:通过变分原理,将Ax=b构造成一个函数,通过对函数的操作,求解Ax=b的解。
1.通过构造函数(变分法),求解方程的解。对于常系数方程2x=2,很容易看出解为1,但是通过构造如何求解
f(x)=x^2-2x
该方程的导数f‘(x)=2x-2=0时,x的解就是2x=2的解。
对于计算机迭代求解,找到f(x)的极值点,就找到了该解。
2.变分原理(构造一个函数,其导数是Ax=b)
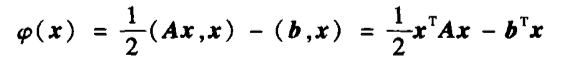
分解一下:下面公式是线性代数中的正定二次型(《线性代数》高等教育出版社 第五版)

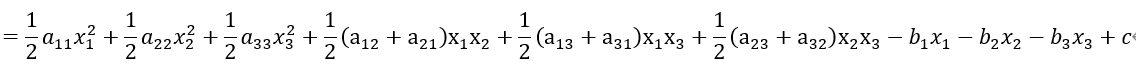

偏导数(梯度)就是Ax=b
换言之,当w(x)取得极值的时候,对应导数=0。
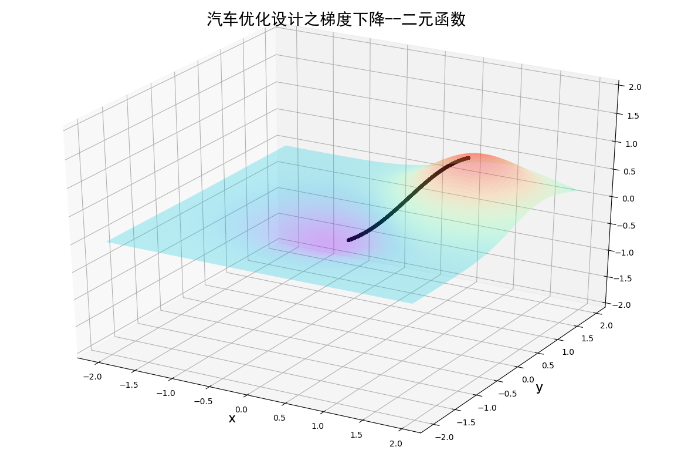
3.最速梯度法(梯度下降发):利用迭代求多元二次函数的极值点。极值点的一阶导数=0.
梯度下降法应用比较广泛,当前热点人工智能的底层匀速基础,就是采用的这个算法。理论推导及示例这里就不啰嗦了。
参考BP神经网络反向传播推导:https://www.cnblogs.com/liuhuacai/p/11973036.html
4.共轭梯度下降法:
公式推导就不贴出来了(贴出来也很费解),直接用一个实例,进行说明。
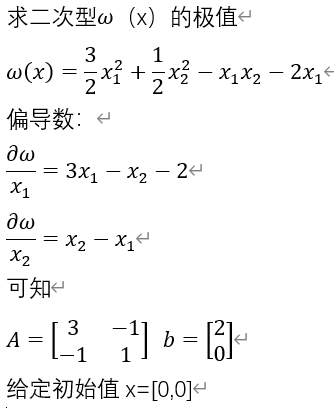
1.先判断这个值是否是极值点,偏导数是否是零(近似数)
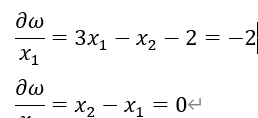
2.在初始值的基础上,x向什么方向移动,可以使函数的值变小(不断迭代,寻找最小值)
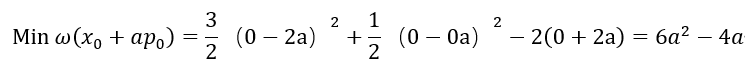

当步长a=1/3时 w(x)向更小值移动一步。
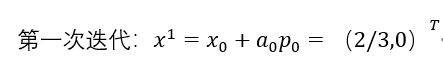
重复上面的步骤,可得到w(x)的极小值点,也就是Ax=b的解。
【理论推导 ,见《数值分析》】