Part 9 常微分方程基础

常微分方程

（柳斌）
主要考虑微分方程的解法，而不考虑理论问题。在数学系需要有一个学期的课程进行专题学习。

数学史引入

Newton第二定律：

$m\frac{\mathrm d^2x}{\mathrm dt^2}=F(t,\overrightarrow{x},\overrightarrow{\dot{x}})$
就是一个关于 $x$的微分方程

万有引力

利用Newton第二定律
地球所受的万有引力可以近似表示成：
$G\frac{m_mm_e}{|x_m-x_e|^2}\frac{x_m-x_e}{|x_m-x_e|}+G\frac{m_sm_e}{|x_s-x_e|^2}\frac{x_s-x_e}{|x_s-x_e|}=m_e\frac{\mathrm d^2 x}{\mathrm dt^2}$

常微分方程的贡献者

• Bernoulli家族
• Euler
• Lagarange
• Gauss

一个突破

Liouville发现， $y'=x^2+y^2$这样一个右端很好的函数无初等函数解。
所以我们的微分方程求解转化到通过方程得出解的一些好性质的阶段。
我们的讨论仅限于之前的可计算的问题。

定义

微分方程

含有未知函数及其至 $n$阶导数的方程
$F(x,y,y',\cdots, y^{(n)})（x\in\R）(1)$
称为一个 $n$阶常微分方程。其中各个函数都在对应相同的 $x$处取值。

阶数等于方程中最高阶导数的阶数。

例：

1. $\frac{\mathrm dy}{\mathrm dx}=y(x-1)$不是微分方程，因为其中出现了非 $x$的变量（式中 $y(x-1)$是 $y$在 $x-1$处的取值）
2. $\frac{\mathrm dy}{\mathrm dx}=y(y(x))$不是微分方程。因为函数关系不明确。

方程的解

称 $y=\varphi(x), x\in(a,b)$是(1)的解，如果 $\varphi$有直到 $n$阶导数，且 $F(x,\varphi(x), \varphi'(x), \cdot\varphi^{n}(x))\equiv0, x\in(a, b)$。

说人话：将函数代入微分方程使得方程成为恒等式，这个函数就是这个方程的解。换言之，微分方程的求解，是利用函数和函数导数关系，求得一个函数作解。

解 $y=c_1+c_2t-\frac{1}{2}gt^2,c_1c_2$为常数。

通解

称 $y=\varphi(x,c_1,c_2,\cdots c,_n)$为方程的通解，如果

1. $y=\varphi(x,c_1,c_2\cdots, c_n)$是解。
2. $c_1,\cdots, c_n$是独立的常数（大致理解，这些常数通过积分产生）。

有时候通解不能通过显函数的方式得到，那么利用隐函数形式表达的通解叫做通积分。

方程特解中常数独立性的判别

Jacobi矩阵
$\left( \begin{matrix} \frac{\partial \varphi}{c_1} &\frac{\partial \varphi}{c_2} &\cdots & \frac{\partial \varphi}{\partial c_n}\\\\ \frac{\partial \varphi'}{\partial c_1} & \frac{\partial \varphi'}{c_2} & \cdots & \frac{\partial \varphi'}{\partial c_n}\\\\ \vdots & \vdots & \ddots & \vdots\\\\ \frac{\partial \varphi^{(n-1)}}{c_1}&\frac{\partial \varphi^{(n-1)}}{\varphi c_2}&\cdots&\frac{\partial \varphi^{(n-1)}}{\partial c_n}\\ \end{matrix} \right)$
不为零可以判别微分满秩。从而得知这些常数不相关。

反向理解：如果其中任意两个常数存在关联，那么它们所在的两列线性相关。从而为0
留待思考：如果求出的Jacobi式是一个和主元有关的式子，那么是否会影响通解各常数之间的独立性。

例如：对方程 $y''+y= 0$我们可以写出特解 $y=\sin x$或 $y=\cos x$，通解 $y=c_1\sin x+c_2\cos x$
但反智的一点是，存在不能通过特解中常数取特殊值将特值表出的情况。这些解叫做“奇解”。

初值问题

初始条件与特解的关系
初始条件确定特解：确定了通解中的常数之后，解成为了特解。
研究添加初始条件后被赋予特定意义、解中的常数得到确定的问题，就是初值问题。

例 $\frac{\mathrm d^2x}{\mathrm dt^2}=-g,\frac{\mathrm dx}{\mathrm dy}=-gt+c_2,x=-\frac{1}{2}gt^2+c_2t+c_1$
如果有一个初态 $x=h,\frac{\mathrm dx}{\mathrm dt}=0$，那么 $h=c_1,\frac{\mathrm dx}{\mathrm dt}=-gt+c_2$解得： $c_2=0$

$y(x_0)=y_0,y'(x_0)=y'_0\cdots y^{(n-1)}=y_0^{(n-1)}$

补充：常微分方程的解的图形叫做积分曲线。

一阶微分方程的求解

任何研究都应该从最基本，最直观的情形开始。一开始也不要用特例情况自我束缚、对思维节外生枝。不妨在解决主要问题之后，再来“修补”这些。

重点也只有三大类：即可变量分离的方程、齐次微分方程、一阶线性微分方程。

变量分离的方程

形如 $y'=f(x)g(y)$的方程可以化成 $F(x)\,\mathrm dx=G(x)\,\mathrm dx$的形式，其中方程右侧是 $x，y$分别的函数的乘积。
解
$\frac{\mathrm dy}{\mathrm dx}=f(x)g(y)\\ \frac{\mathrm dy}{g(y)}=f(x)\,\mathrm dx\\ \int\frac{1}{g(y)}\,\mathrm dy=\int f(x)\,\mathrm dx$
这一步先不考虑特殊情况即能不能除，找准主要思路。记
$G(y)=\int\frac{1}{g(y)}\,\mathrm dy\\ F(x)=\int f(x)\,\mathrm dx\\ G(y)=F(x)$
这是一个代数方程

现在重新考虑不能相除的情况，即 $\exist b\,s.t.g(b)=0$，那么 $y\equiv b$是特解（千万不要忘记啊！）

例 $y'=\alpha y(\alpha$是常数)
$\frac{1}{y}\,\mathrm dy=\alpha\,\mathrm dx\\ \ln|y|=\alpha x+C\\ |y|=e^c\cdot e^{\alpha x}=C_1\cdot e^{\alpha x}\\ y=C\cdot e^{\alpha x}(c\not=0)$
加上特解 $y\equiv0$，原方程的解可以表示成 $y=C\cdot e^{\alpha x}$

将方程化为变量分离的

$1^。$形如
$\frac{\mathrm dy}{\mathrm dx}=f(ax+by+c)$
的方程：
引入 $u=ax+by+c,$
$\begin{aligned} &\frac{\mathrm du}{\mathrm dx} =a+b\frac{\mathrm dy}{\mathrm dx}\\ =&a+bf(ax+by+c)\\ =&a+bf(u) \end{aligned}$
显然 $u$是可解的。 $u=u(x,\tilde{c})$
这又是一个代数方程。

特别注意在求解过程当中，要将 $f(u)=0$的情况考虑成一个奇解。

$2^\circ$
“一阶导数导数=零次齐次函数”的齐次方程

$n$次齐次函数定义为： $\varphi\left(\frac{ty}{tx}\right)=t^n\left(\frac{y}{x}\right)$
$y'=f\left(\frac{y}{x}\right)(x\not=0)$

令 $u=\frac{y}{x},y=xu,\frac{\mathrm dy}{\mathrm dx}=\frac{\mathrm d}{\mathrm dx}(xu)=u+x\frac{\mathrm du}{\mathrm dx}\xlongequal{y'=f(u)}f(u)$
由于 $x\not=0$， $\frac{\mathrm du}{\mathrm dx}=\frac{f(u)-u}{x}$

$3^\circ$另一类齐次
$y=f\left(\frac{a_1x+b_1y+c_1}{ax+by+c}\right)$

1. 若 $c=c_1=0, y'=f\left(\frac{a_1x+b_1y}{ax+by}\right)=f\left(\frac{a_1+b_1\frac{y}{x}}{a+b\frac{y}{x}}\right)=g(\frac{y}{x})$
2. 若不全为0.那么做平移变换。

$\begin{cases} x=u+\alpha\\ y=v+\beta \end{cases}\\ s.t.\, a_1\alpha+b_1\beta+c_1=0\\ a\alpha+b\beta+c=0$
则
$\frac{\mathrm dv}{\mathrm du}=f\left(\frac{a_1u+b_1v}{au+bv}\right)$
利用Cramer法则，
$\begin{vmatrix} a_1&b_1\\ a&b \end{vmatrix}\not=0$
时， $\alpha, \beta$存在且唯一，可解。
$\begin{vmatrix} a_1&b_1\\ a&b \end{vmatrix}=0$
时，设 $\frac{a_1}{a}=\frac{b_1}{b}=k$
$y'=f\left(\frac{a_1x+b_1y+c_1}{ax+by+c}\right)=f\left(\frac{k(ax+by)+c_1}{ax+by+c}\right)$
现令
$\frac{\mathrm du}{\mathrm dx}=a+b\frac{\mathrm dy}{\mathrm dx}=a+bf(\frac{ku+c_1}{u+c})$
变量分离，又是可解的。
$\frac{\mathrm d y}{\mathrm dx}=\frac{x+y+2}{x-y+1}$

一阶线性方程

$y'+p(x)y=q(x), p,q\in C^0(a,b)$
(1)
其中的 $C^0$表示连续， $C^1$表示连续可微。

一阶线性方程的判别

关于未知函数 $y$与其导数 $\frac{\mathrm dy}{\mathrm dx}$都是一次的。如果 $q(x)=0$成为一阶齐次线性微分方程，否则成为一阶非齐次。

一阶线性方程的计算

$1^\circ$ 最简单的情况： $q(x)=0$（齐次）

这个“齐次"和我们前述的齐次函数的齐次并不相同。
$y'+p(x)y=0$
(2)
$\frac{\mathrm dy}{\mathrm dx}=-p(x)y$
首先我们发现 $y=0$是一个奇解。然后移项积分：
$ln|y|=-\int_{x_0}^xP(t)\,\mathrm dt+C$
$y=\pm e^c e^{\left(-\int_{x_0}^xP(t)\,\mathrm dt\right)}$
结合奇解
$y=C\cdot e^{\left(-\int_{x_0}^xP(t)\,\mathrm dt\right)},\forall C$
这个结果告诉我们，线性齐次方程的解仅有两种情况： $\equiv0$或 $\not\equiv0$，
讨论：

• $\varphi_1(x), \varphi_2(x)$是（2）的两个解，那么 $\forall k_1,k_2\in\R, k_1\varphi_1+k_2\varphi_2$是 $(2)$的解。
• 若 $\varphi(x)$是（2）的解，则 $\varphi(x)\in C(a,b)$
• 一般非线性方程可能存在解的长度比定义域长度短的情况。例： $y'=1+y^2, y=\tan x, x\in(-\frac{\pi}{2}, \frac{\pi}{2})$，对于线性，一定是一样长的。

$2^\circ$非齐次

解的性质：

• 若 $y=\varphi(x),y=\psi(x)$是（1）的解，则 $y=\varphi(x)-\psi(x)$是（2）的解
• 若 $y=\varphi(x)$是（1）的解， $y=\Phi$是（2）的解，那么 $y=\varphi(x)+\Phi(x)$是（1）的解。

求解思路：

• 从而推知若 $y=\varphi(x)$是（1）的一个解。那么（1）的所有解可以写成 $y=\varphi(x)+Ce^{-\int_{x_0}^xP(t)\,\mathrm dt}$
• 由上述，这个方程的求解转化成求解(1)的一个特解。

方法：常数变易法

将齐次方程的解中的常数变成一个函数表达式，待定为 $u(x)$
$y'=u'(x)\cdot e^{-\int_{x_0}^xP(t)\,\mathrm dt}-u(x)P(x)e^{-\int_{x_0}^xP(t)\,\mathrm dt}=Q-P(x)y$
化简得：
$u'(x)\cdot e^{-\int_{x_0}^xP(t)\,\mathrm dt}=Q$
$u'(x)=Q(x)\cdot e^{\int_{x_0}^xP(t)\,\mathrm dt}$
这个式子可不可积其实还有待讨论……但总之把它积起来就可以得到我们需要的 $u(x)$
$y=\left[\int_{x_0}^xQ(t)e^{\int_{x_0}^tP(s)\,\mathrm ds}\,\mathrm dt+C\right]e^{-\int_{x_0}^xP(t)\,\mathrm dt}$

步骤整理：

• step1：求齐次方程通解 $C\cdot y_1(x)$
• step2： $u'=\frac{Q(x)}{y_1(x)}$
• step3：移项积分，整理得解

若 $f\in C(a, +\infty)$且 $f(x)+f'(x)\to0$则 $f(x)\to0$

另例：
$f(x)\in C^1[0,+\infty), a(x)\geq C_0>0, a(x)\in C[0,+\infty)$且 $\lim\limits_{x\to+\infty}(f'(x)+a(x)f(x))=0$则 $\lim\limits_{x\to+\infty}f(x)=0$

令 $b(x)=f'(x)+a(x)f(x), b(x)\in C^0[0,+\infty),\lim\limits_{x\to+\infty} b(x)=0$，从 $b$中解出 $f(x)$
$f(x)=Ce^{-\int_{x_0}^xa(t)\,\mathrm dt}+e^{-\int_{x_0}^xa(t)\,\mathrm dt}\cdot \int_0^xb(s)e^{\int_0^sa(t)\,\mathrm dt}\,\mathrm ds$
其中取初值条件，可以得 $C=f(0)$
$f(x)=\frac{f(0)+\int_0^xb(s)e^{\int_0^sa(t)\,\mathrm dt}\,\mathrm ds}{e^{\int_0^xa(t)\,\mathrm dt}}$
分母趋向于无穷（且求导后无穷，即满足洛必达法则），
即有 $\lim\limits_{x\to+\infty}f(x)=\lim\limits_{x\to+\infty}\frac{b(x)}{a(x)}=0$

$3^\circ$Bernoulli方程

这是一个将非线性方程化成线性方程的好例子。
$\frac{\mathrm dy}{\mathrm dx}+P(x)y=Q(x)y^\alpha$
$y^{-\alpha}\frac{\mathrm dy}{\mathrm dx}+P\cdot y^{1-\alpha}=Q(x)$
令 $z=1-\alpha$,
$\frac{1}{1-\alpha}\frac{\mathrm dz}{\mathrm dx}+P(x)z=Q(x)$
这是一个线性方程。

全微分方程

全微分方程的形式

$\frac{\mathrm dy}{\mathrm dx}=-\frac{P}{Q}$
对称形式
$P(x,y)\,\mathrm dx+Q(x,y)\,\mathrm dy=0$

$P,Q\in C^1(D)$(这里要可微，因为如果不可导的话，我们的方法实在有限)

若 $\exist F(x,y)\in C^1(D), \,\mathrm dF(x,y)=P\,\mathrm dx+Q\,\mathrm dy\Rightarrow \mathrm dF(x,y)=0$

从而我们求这样的方程的解的问题，转化成：

1. 判断 $F$的存在性
2. 求出 $F$

在二型线和路径无关的条件时，我们写出了几个这个 $F$存在的等价条件。
在这里我们常用
$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$
必要性利用连续函数的混合导数相等说明。

判别条件的充分性证明：

偏积分得
$F=\int_{x_0}^xP(s,y)\,\mathrm ds+\varphi(y)$
(1)
$Q=\frac{\partial}{\partial y}\int_{x_0}^xP(s,y)\,\mathrm ds+\varphi'(y)$
由于光滑，求导积分可交换。
$Q=\int_{x_0}^x\frac{\partial}{\partial y}P(s,y)\,\mathrm ds+\varphi'(y)$
再由充分条件得：
$\int_{x_0}^x\frac{\partial}{\partial x}Q(s,y)\,\mathrm ds+\varphi'(y)=Q(x,y)$
$Q(x,y)-Q(x_0,y)+\varphi'(y)=Q(x,y)$
得
$\varphi'(y)=Q(x_0,y)$
$\varphi=\int_{y_0}^yQ(x_0,t)\,\mathrm dt$
结合（1）得:
$F(x,y) =\int_{x_0}^xP(s,y)\,\mathrm ds+\int_{y_0}^yQ(x_0,t)\,\mathrm dt$
说人话，就是说明了二型线与路径无关的条件是全微分方程直接用原函数是解的条件。

例 $(x\cos y+2xy^2)\,\mathrm dx+(-\frac{1}{2}x^2\sin y+2x^2y+y^2)=0$
$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$然后使用偏积分求出通积分。

接下来要解决的问题是，如果 $\frac{\partial P}{\partial y}$和 $\frac{\partial Q}{\partial x}$不相等呢？

积分因子

对以上的问题，基本想法是：
寻找一个（就够的） $\mu=\mu(x,y)\not=0$s.t.
$\mu P\,\mathrm dx+\mu Q\,\mathrm dy=0$
是全微分方程。

$\mu$满足 $\mu P=\frac{\partial F}{\partial x}, \mu Q=\frac{\partial F}{\partial y}$

结合光滑：
$\frac{\partial }{\partial y}(\mu P)=\frac{\partial }{\partial x}(\mu Q)$
转化成：

$P\frac{\partial \mu}{\partial y}-Q\frac{\partial \mu}{\partial x}=\mu\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)$

这是一个一阶偏微分方程。
但我们仍只需要找到一个就够。

若存在 $\mu=\mu(x)$
$\frac{\mu'}{\mu}=-\frac{\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}}{Q(x,y)}$
若右端只依赖 $x$那么就是变量分离的方程，可求这个积分因子。
$\mu=e^{\int_{x_0}^xf(s)\,\mathrm ds}$
实际求解过程中，我们只需要看 $P,Q$二者谁和右端相除可以化成单变量式。

附：另一个常用的表达式；
$\frac{\mu'}{\mu}=\frac{\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial x}}{P(x,y)}$

微分方程解的存在、唯一性定理

如果方程
$\begin{cases} y'=f(x,y)\tag1\\ y(x_0)=y_0 \end{cases}$
若 $f$连续，且满足Lipschitz条件（斜率不大于某个值）：
$\exist L>0,\forall(x,y_1),(x,y_0)\in D$
$|f(x,y_0)-f(x,y_1)|\leq L|y_1-y_0|$
那么其在 $|x-x_0|\leq h$解存在且唯一
$\begin{aligned} h=&\min\{a,\frac{b}{M}\}\\ M=&\max\limits_D|f(x,y)| \end{aligned}$

• 注1： $h$是越界保护。其中 $M$通过(1)中代换得到的： $y'\leq M$。

证明：
Step1：
原式等价于
$y(x)-y_0=\int_{x_0}^xf(s,y(s))\,\mathrm ds$
Step2：
构造Picard序列：
$\varphi_{n+1}(x)=y_0+\int_{x_0}^xf(s,\varphi_n(s))\,\mathrm ds$
这也是近似求解的方法。逐次逼近为我们提供了一种求近似解的计算方法。

Step3：
序列一致收敛，故存在（证明略

Step4：
解的唯一性判定
$|\varphi(x)-\psi(x)|\leq \left|\int_{x_0}^xf(s,\varphi(s))-f(s,\psi(s))\,\mathrm ds\right| \leq L\int_{x_0}^x|\varphi(s)-\psi(s)|\,\mathrm ds$
$|\varphi(x)-\psi(x)|\leq LM_0|x-x_0|$
故（2）代入（1）得
$|\varphi(x)-\psi(x)|\leq \frac{L^2M_0}{2}|x-x_0|^2$
累次代入，得：
$|\varphi(x)-\psi(x)|\leq\frac{L^nM_0}{n!}h^n$
显然，
$\varphi(x)\equiv\psi(x)$

注1（Cauchy条件）
$f\in C^1(D)$
$f(x,y_1)-f(x,y_2)=\frac{\partial f}{\partial y}(x,\xi)(y_1-y_0)$
显然这是满足Lipschitz条件的。

注2 满足Lipschitz条件的未必处处可微。例如 $f(x,y)=|y|$

推论：对 $y'=f(x,y),(x,y)\in D$，若函数 $f(x,y)$和 $f_y$在区域上连续，那么过D内任一点 $(x_0,y_0)$，有且仅有一条方程的积分曲线通过。（利用Cantor定理可说一致连续）

注3 虽然Picard定理所求的范围有限。但是我们可以通过不断的延拓，仍能获得很好的结果

高阶举例——二阶方程的求解

$y''(x)+p(x)y'(x)+q(x)y(x)=f(x)\tag3$
$y''(x)+p(x)y'+q(x)y=0\tag4$
性质1：显然（4）的解具有线性性质。

对于二阶方程，我们首先有这样一类容易解决的问题。

可降阶的方程

这是解决高阶方程的一个很简便、清晰的思路。但条件有限制。

常用 不显含 $x$的二阶方程（通常设题比较刁钻，只能用此法解）
$F(y,y',y'')=0$
令
$P=y'=\frac{\mathrm dy}{\mathrm dx}$
$y''=\frac{\mathrm d}{\mathrm dx}y'=\frac{\mathrm d}{\mathrm dy}y'\frac{\mathrm dy}{\mathrm dx}=\frac{\mathrm dP}{\mathrm dy}P$
原式可以转化为
$F_1(y,P,\frac{\mathrm dP}{\mathrm dy})=0$
这是一阶线性方程。
所得解 $P=\frac{\mathrm dy}{\mathrm dx}$又是变量分离的。

另外还有 $F(x,y',y'')=0$型（将 $y'$记为 $P$）。

这是一个快捷化简。

函数的线性相关

判据——W行列式

其他的方程在求解上具有一定的复杂性，不能通过初等方法求解，但我们可以通过一定的方式对其解的结构进行研究。

设 $g_1(x),g_2(x)\in D(a,b),\exist c_1,c_2,s.t.\,\urcorner(c_1=0\wedge c_2=0)\wedge c_1g_1+c_2g_2\equiv0$则称 $g_1,g_2$线性相关。
结合性质1，我们提出以下引理：
设 $\varphi_1(x), \varphi_2(x)$是（4）的两个解。那么它们在 $(a,b)$上线性相关的充要条件是：它们确定的Wronski行列式
$W=\begin{vmatrix} \varphi_1&\varphi_2\\ \varphi_1'&\varphi_2' \end{vmatrix}\equiv0$
证明：必要性对（4）和（4）的一阶导数式利用Cramer法则。充分性利用解的存在唯一性。详见高数下P180

Wronski行列式的计算

$w(x)=\varphi_1(x)\varphi_2'(x)-\varphi_2(x)\varphi'_1(x)\\ w'(x)=\varphi'_1\varphi'_2+\varphi_1\varphi_2''-\varphi'_2\varphi_1'-\varphi_2\varphi''_1=\varphi_1\varphi''_2-\varphi_2\varphi_1''$
方程组的秩为3，三个变量，可解。
$\varphi''_1+p\varphi'_1+q\varphi_1=0\\ \varphi_2''+p\varphi'_2+q\varphi_2=0$
代入消元可得：
$w'=p\cdot(-w)$
解这个变量分离的方程有：
$w(x)=w(x_0)e^{-\int_{x_0}^xp(s)\,\mathrm ds} (Liouville公式)$
这个公式告诉我们，在待求区间 $(a,b)$上如果有一点的Wronski行列式为0，那么整个区间上都为零。

二阶线性齐次微分方程

前面已经讨论了函数线性无关的条件。

对于方程（4），我们只需要找到两个线性无关的解，这两个解的初值分别为 $(0,1)$和 $(1,0)$，
那么所有解都可以经由这两个解表出。

为什么是两个？二阶方程看似是三个不定元，但实际上方程会隐式地确定 $x$，所以只要将带有积分常数 $C$的 $y,y'$的初值确定下来，那 $y''$也就是唯一确定的了。所以这个方程如果展成方程组，对于 $y^{(n)}$结构来看，显示的秩只有 $n-1$。因而我们只需求解两个初值即可。

求解二阶线性非齐次方程

$y''+p(x)y'+q(x)y=f(x)\tag3$
设 $y=\varphi_1(x), y=\varphi_2(x)$是（4）的线性无关解。
$y=\varphi_0(x)$是（3）的一个特解。

则（3）的所有解都可以表示成：
$y=c_1\psi_1(x)+c_2\psi(x)+\varphi_0(x)$
这仍然是由方程的线性性质所保证的。
求解过程就退化成找特解。

为了扩大可解的范围，我们给出如下的

分治定理

设 $y=\varphi_1(x)$是
$y''+py+qy=f_1$
的解，
设 $y=f_2(x)$是
$y''+py'+qy=f_2$
的解。

那么 $\varphi_1+\varphi_2$是原方程的解。
这为分治的思路提供了指导。

在正式研究求解之前，我们给出关于可解性的一般规律：如果 $p,q$与 $x$有关，一般不可解。
例如：
$y''+a(x)y=0\\ a(x)=1+\varepsilon\cos x$
除了 $y\equiv0$以外我们找不到其他的有用的解。所以接下来，我们着重讨论二阶方程一种比较简单的形式：

二阶常系数微分方程

$y''+py'+qy=f(x)\tag5$
核心思想是尝试，方法是待定系数法。找到线性无关的解基，我们就赢了。

首先解决齐次情形：
这里考虑到 $e$指数函数的求导性质优良，我们优先考虑形如 $y=e^{\lambda x}$的解。代入得：
$(\lambda^2+p\lambda+q)e^{\lambda x}=0$
$e^{\lambda x}$是解 $\Leftrightarrow \lambda^2+p\lambda+q=0$

case 1：特征根相异时 $y_1=e^{\lambda_1 x},y_2=e^{\lambda_2x}$是两个线性无关的解
$W(x)=\begin{vmatrix} e^{\lambda_1x}&e^{\lambda_2x}\\ \lambda_1e^{\lambda_1x}&\lambda_2e^{\lambda_2x} \end{vmatrix}=(\lambda_2-\lambda_1)e^{(\lambda_1+\lambda_2)x}$

case2：特征根为二重根时。第一个根是容易找到的。常用方法是对另一根进行乘 $x^n$.
这里乘 $x$就够用了 $y_2=xe^{\lambda x}$经验证，也是一个解。
且 $y_1=e^{\lambda_1x},y_2=xe^{\lambda_2x}$可得Wronski行列式不为零。

有了以上的讨论，我们就可以解特征方程 $\Delta >0$的问题了。

case3：特征方程有共轭复根
$\lambda_{1,2}=\alpha\pm i\beta, \beta>0$

$y^*_1(x)=e^{(\alpha+i\beta )x}=e^{(\alpha x}(\cos\beta x+i\sin\beta x)\\ y^*_2(x)=e^{(\alpha-i\beta) x}=e^{\alpha x}(\cos\beta x-i\sin\beta x)$
消虚数，取得两个实函数解基：
$y_1(x)=\frac{1}{2}(y_1^*+y_2^*)=e^{\alpha x}\cos\beta x\\ y_2(x)=\frac{1}{2i}(y^*_1-y_2^*)=e^{\alpha x}\sin \beta x$
由于 $\beta >0$故而Wronski行列式为 $\beta e^{2\alpha x}\not=0$

于是我们可以将通解形式总结为：

特征方程判别式	特征根	通解形式
$\Delta >0$	两个相异实根 $\lambda_1, \lambda_2$	$C_1e^{\lambda_1 x}+C_2e^{\lambda_2x}$
$\Delta = 0$	二重根 $\lambda_1$	$(C_1+C_2x)\cdot e^{\lambda_1}x$
$\Delta <0$	$\lambda_{1,2}=\alpha\pm i\beta$	$e^{\alpha x}(C_1\cos\beta x+C_2\sin\beta x)$

• 从某个角度上说，非重根的所有情况都是第三种情形的退化情况。
• 注意这个 $\beta x$是放在一起写的。这是 $e^{i x}$的De Moivre展开。

其实在常系数的情况下，高阶的也相对容易求解。

特征根	通解
单重实根 $\lambda$	$e^{\lambda x}$
k重实根( $k>1$) $\lambda$	$e^{\lambda x},xe^{\lambda x}, \cdots, x^{k-1}e^{\lambda x}$
单共轭复根 $\lambda_{1,2}=\alpha+i\beta$	$e^{\alpha x}\cos\beta x,e^{\alpha x}\sin\beta x$
$n$重共轭复根 $\lambda_{1,2}=\alpha+i\beta(n>1)$	$e^{\alpha x}\cos\beta x,e^{\alpha x}\sin\beta x, \cdots,x^{n-1}e^{\alpha x}\cos\beta x,x^{m-1}\sin\beta x$

二阶常系数线性非齐次方程

虽然已经研究了关于线性齐次方程的问题。但是，解决大部分非齐次仍然是困难的。
在这里，我们着重讨论以下几种：

1. $f(x)=P_n(x)$
2. $f(x)=a\cdot e^{\alpha x}$
3. $f(x)=a\cos\beta x+b\sin\beta x$

它们的方法都相对固定：核心方法是待定系数，目标是找通解，退化时乘 $x$

我们从最简单的情形开始：

多项式型

利用待定系数法，设解为：
$Q_n(x)=b_0x^n+b_1x^{n-1}+\cdots +b_n, b_0\not=0$
（0不是特征根）case 1:
$q\not=0$时，左右都是 $n$次多项式。比较各次项系数，解出 $b_i$

（0是单特征根）case 2:
考虑 $Q(x)=xQ_n(x)$，代入得：
$Q'(x)=Q_n(x)+xQ_n'(x)\\ Q''(x)=2Q'_n(x)+xQ_n''(x)$
整理出 $n$次项作为首项的式子：
$p(xQ_n'+Q_n)+(xQ_n''+2Q_n')=P_n$
如果 $p\not=0$退化成case 1中的讨论情形。

（0是重特征根）case 3:
对case 3中的 $p=0$情形，考虑 $Q_n(x)=x^2Q_n$可以直接代入对比系数（北大P188）。

史逸老师提供了一种方便的理解，case3包含条件 $p=0,\ q=0$，原式即：
$y''=P_n(x)$
两次积分得：
$y=\int P_{n+1}\,\mathrm dx+C_1x+C_2$

简要(emmm)总结：q!=0? y : (q!=0 ? x.y : xx.y)

常微分方程部分应该多加练习。寻找一种求解的直觉。

$e$指数型

核心思路仍然是待定系数：
$f(x)=a\cdot e^{\alpha x}, a, \alpha\in\R,a\not=0$
设 $y(x)=A\cdot e^{\alpha x}$
原方程转化为：
$(A\alpha^2+pA\alpha+qA)e^{\alpha x}=a\cdot e^{\alpha x}$
（ $\alpha$是特征根）case 1:
若 $\alpha^2+p\alpha+q\not=0$，则
$A^*=\frac{a}{\alpha^2+p\alpha +q}\tag1$
$A^*\cdot e^{\alpha x}$为一个特解。

（ $\alpha$是单特征根）case 2:
若 $\alpha^2+p\alpha+q=0$，则。。。没那么简单

同样使用乘 $x$的方法， $y=Axe^{\alpha x}$，原式即：
$Ae^{\alpha x}\left[(\alpha^2+p\alpha+q)x+(2\alpha+p)\right]\\ Ae^{\alpha x}\left(2\alpha+p\right)=ae^{\alpha x}$
（ $\alpha$不是重根）再分两种情况： $2\alpha+p\not=0$直接找到一个特解
$\frac{a}{2\alpha+p}\tag2$

（ $\alpha$是重根）若 $2\alpha+p=0$，则 $\alpha$为 $\lambda^2+p\lambda+q=0$的重根。此时 $Axe^{\alpha x}$仍然不是满足条件的特解。我们还需要构建一个新的形式的解。

设 $Ax^2e^{\alpha x}$，代入得
$Ae^{\alpha x}\left[(\alpha^2+p\alpha +q)x^2+(4\alpha+2p)x+2\right]\\ =2Ae^{\alpha x}=ae^{\alpha x}$

即
$y=\frac{a}{2}x^2e^{\alpha x}\tag3$
为一个特解.

三角型

设 $y=A\cos\beta x+B\sin\beta x$

代入得：
$(-A\beta^2+pB\beta+qA)\cos\beta x+(-B\beta^2-pA\beta+Bq)\sin\beta x=a\cos\beta x+b\sin \beta x$

转化为方程
$(q-\beta^2)A+p\beta B=a\\ -p\beta A+(q-\beta^2)B=b$
由Cramer法则
$\Delta =(q-\beta)^2+p^2\beta^2\not=0$
case 1：
如果 $\Delta \not=0$，那么有唯一解。记作
$A^*\cos\beta x+B^*\sin\beta x$
case2：
（ $\beta i$是特征根）如果 $q-\beta^2$与 $p\beta$同时为0
设 $y=x(A\cos\beta x+B\sin\beta x)$
代入得：
$\begin{cases} pA+2\beta B=a\\ -2\beta A+pB=b \end{cases}$
由Cramer法则，方程有唯一解。
$y=x(A^*\cos\beta x+B^*\sin\beta x)$
就是特解。

其他组合

除了以上三种，我们有以下可解的组合情况
$P_n(x)e^{\alpha x}(\alpha \cos\beta x+b\sin\beta x)$
如果 $\alpha\pm i\beta$不是特征根， $e^{\alpha x}[Q_n(x)\cos\beta x+R_n(x)\sin\beta x]$，如果是特征根（退化情况就乘 $x$即可），即： $e^{\alpha x}[Q_n(x)\cos\beta x+R_n(x)\sin\beta x]$

这个结合分治定理便可以解决大量的非齐次问题了。

比如这个例子
$y''+y=x\cos 2x+\sin x$
利用分治定理我们就可以化成我们熟悉的形式了。

补充：
为什么最后的总结我们将判别条件利用是否为特征根表达? 做题真的很方便啊！

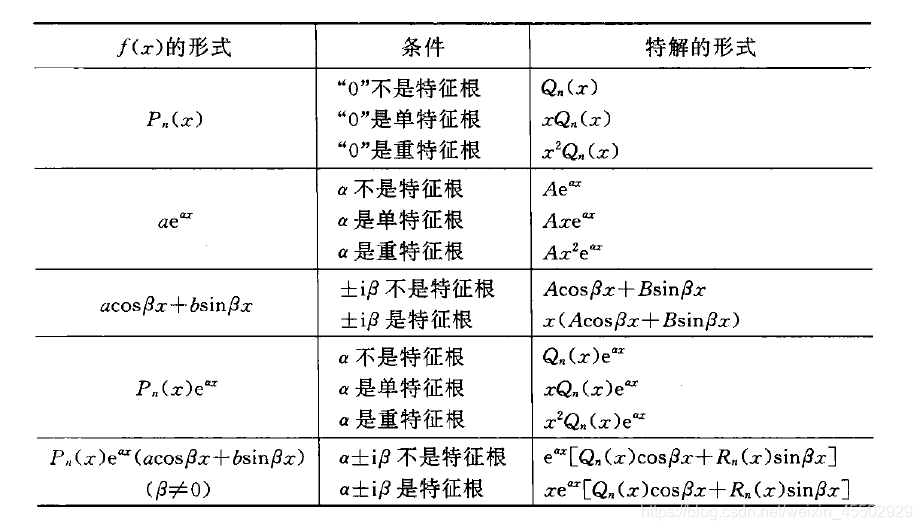
常数变易法

当右式不是以上讨论的几种类型的时候，我们需要使用先哲发现的伟大通解法：常数变易法。

常数变易法是解线性微分方程行之有效的一种方法。它是拉格朗日十一年的研究成果，我们所用仅是他的结论，并无过程。

常数变易，顾名思义就是将本来是常数的部分变成函数。即：
设
$y(x)=C_1(x)\varphi_1(x)+C_2(x)\cdot\varphi_2(x)$
是
$y''(x)+p(x)y'(x)+q(x)y(x)=f(x)\tag{*}$
的一个解。
$\begin{aligned} y'(x)&=C_1(x)\varphi_1'(x)+C_2(x)\varphi'_2(x)\\ &+C_1'(x)\varphi_1(x)+C_2'(x)\varphi_2(x) \end{aligned}$

令：
$C_1'(x)\varphi(x)+C_2'(x)\varphi_2(x)=0\tag1$
便有
$y'(x)=C_1(x)\varphi_1'(x)+C_2(x)\varphi_2'(x)$
再求导
$y''=C_1(x)\varphi_1''(x)+C_2(x)\varphi_2''(x)+C_1'(x)\varphi_1'(x)+C_2'(x)\varphi_2'(x)$
注意到 $\varphi_1(x)$与 $\varphi_2(x)$是齐次方程的解：
$C_1'(x)\varphi'_1(x)+C_2'(x)\varphi_2'(x)=f(x)\tag2$
联立(1)(2)，是一个Wronski行列式不为零的方程组，可解 $C_1',C_2'$
关于常数变易法，我们特别注意的公式是：
$\begin{cases} C_1'(x)\varphi_1(x)+C_2'(x)\varphi_2(x)=0\\ C_1'(x)\varphi_1'(x)+C_2'(x)\varphi_2'(x)=f(x) \end{cases}$

Euler方程

一类可以化成常系数方程的线性变系数方程。（但方法固定，考察并不多）
$a_0x^ny^{(n)}+a_1x^{n-1}y^{(n-1)}+\cdots+a_{n-1}xy'+a_ny=0$
其中 $a_i(i=0,1,2\cdots)$为常数

方法：
代入 $x=e^t$，然后就可以化成常系数线性微分方程，通解公式为：
$x^ky^{(k)}=D(D-1)\cdots(D-k+1)y$
其中 $D$为微分算符 $\frac{\mathrm d}{\mathrm dt}$

这个 $D$的次数直接对应为微分方程中对应项的次数。

常系数线性微分方程组

基本概念

• 常数的独立性利用Jacobi行列式检验。
• 特解（代入后使得每一个方程成为恒等式的函数组），通解（带有n个独立的任意常数的函数组），向量函数
• 唯一性定理：只要n个初值给定，就存在唯一

几种低阶的解法

二阶

代入法，保留一个，消去一个从而成为二阶线性方程

三阶

讨论是否有两个元的系数成比例：
利用Wronski行列式

• 有两个变量的系数成比例：先解另一个变量的二阶线性方程
• 均不成比例：不妨设 $x,y,z$，那么先用 $x$及其导数表示 $y,z$然后得到 $x$的三阶方程。