常微分方程的数值求解

常微分方程

首先理解一下什么是常微分方程,简单的说就是只有一个未知数的微分方程,具体定义如下:
凡含有参数，未知函数和未知函数导数 (或微分) 的方程，称为微分方程，有时简称为方程，未知函数是一元函数的微分方程称作常微分方程，未知函数是多元函数的微分方程称作偏微分方程。
一阶常微分方程的初值问题是:

$$\begin{cases} y' =f(x,y) ,\\ y(x_0)=y_0, \end{cases}$$

其中$y=y(x)$是未知函数,$y(x_0)=y_0$是初值条件,而$f(x,y)$是给定的二元函数

---

简单的数值方法和欧拉公式

简单的数值方法就是用差商代替导数,公式如下:

$$y_{n+1}=y_n+hf(x_n,y_n) \quad (n=0,1,2,\cdots)$$
其中 $h$是步长;
改进的欧拉方法:
$$\begin{cases} \bar y_{n+1}=y_n+hf(x_n,y_n) &\text{预测} \\ y_{n+1}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},\bar y_{n+1})] &\text{校正} \end{cases}$$

---

龙格-库塔(Runge-Kutta)方法

欧拉方法是龙格-库塔方法的一个特例,其局部截断误差为一阶泰勒余项$O(h^2)$,为了使误差更小,我们可以做更高阶的误差截断,这也就是我们Runge-Kutta方法的基本原理,具体推导可参考《数值分析》的第八章.其公式如下:

$$\begin{cases} y_{n+1}=y_n+h \sum_{i=1}^r c_iK_i, \\ K_1=f(x_n,y_n),\\ K_i=f(x_n+\lambda_ih,y_n+h\sum_{j=1}^{i-1}u_ijK_j) \quad (i=2,3,\cdots,r), \end{cases}$$
当r=1时就是欧拉方法,当r=2时,就是改进的欧拉方法,这里我们不做具体推导,而是看一下matlab中封装好的4阶Runge-Kutta方法的函数实现ode45函数.

---

ode45

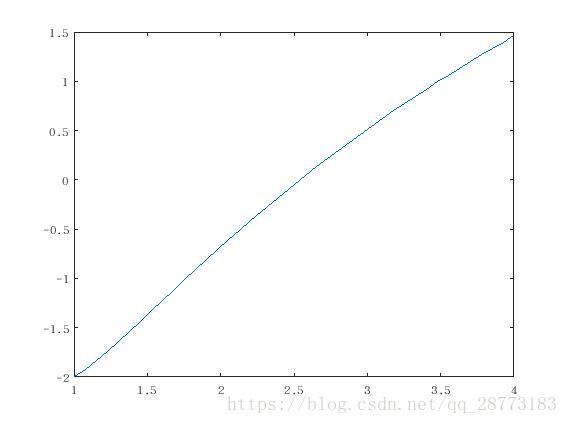
先看一个简单的例子:$\frac{dy}{dx}=\frac{y+3x}{x^2}$,初值$y(0)=-2$,求解区间为$[1 4]$,代码如下:

odefun=@(x,y) (y+3*x)/x^2;
tspan=[1 4];
y0=-2;
[x y]=ode45(odefun,tspan,y0)
plot(x,y)

但是我们再看另外一个例子:

$$\begin{cases} y'=\frac{y}{x}-2y^2\quad \text{0<x<3}\\ y(0)=0 \end{cases}$$
我们编写如下代码:

odefun=@(x,y) y/x-2*y^2;
tspan=[0 3];
y0=0;
[x y]=ode45(odefun,tspan,y0)
plot(x,y)
disp(y)

发现没有数值解

于是我们把代码进行了如下修改:

odefun=@(x,y) fun(x,y);
tspan=[0 3];
y0=0;
[x y]=ode45(odefun,tspan,y0);
plot(x,y)

function dy = fun(x,y)
if(x==0)
    dy=1-2*y^2
else
    dy = y/x-2*y^2
end
end

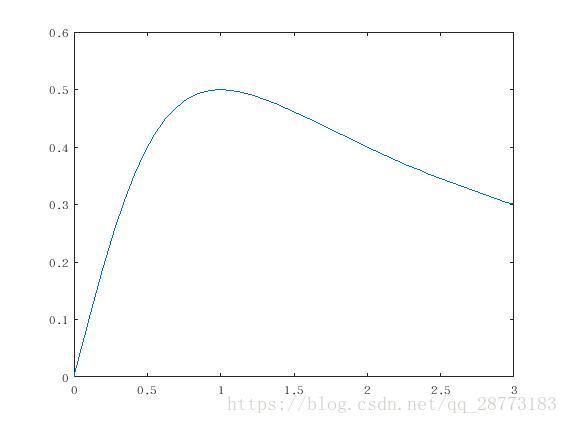
这里需要强调一点的是,Runge-Kutta法针对的是连续的函数$f$,由于在例子中,函数在$x=0$处是不连续的,所以在这个地方是需要单独处理的,在这里,$\frac{y}{x}$在$x=0$处的导数为1(洛必达法则,即$\frac{0}{0}=1$)