LCA最近公共祖先
LCA:树上两个结点的最近公共祖先
适用于求树上某条路径相关的一些问题
方法一:暴力求解
原理:对于已知每个结点的父亲结点的树,要求x和y的LCA,首先让深度更深的结点,此处
不妨设为y,向上跳到与x同样的深度,然后两个结点再同时往上跳,直至重合,这个重合的结点就是x和y的LCA。
缺点:效率低下,一般不使用
代码:
int GetLCA(int x,int y){
if(dep[x]>dep[y]) //令y为更深
swap(x,y);
while(dep[x]<dep[y])
y=fa[y];//让更深的y先往上跳,直到与x相同的高度
while(x!=y) //两者同时上跳,直到重合
x=fa[x],y=fa[y];
return x;
}
方法二:倍增算法(对暴力的优化)
原理:暴力法,单纯地往上跳的方法缺点在于一个一个的跳,时间复杂度过高。那么对于这个跳的过程,可以进行倍增优化,就是每一次跳不止一个结点,这样就可将复杂度降到对数级。
复杂度:O(nlogn+qlogn),n个结点,q次询问
具体实现细节(两部分):
预处理时处理标明结点的深度
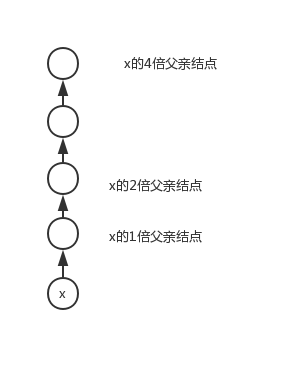
1:预处理。求出每个结点的1,2,4,8......倍父亲结点,具体可以用一个比较简单的DP
复杂度O(nlogn)
const int N=500010;
int fa[N][20];//存2的各个次方倍的父亲结点,fa[i][k]:结点i的2^k父亲结点,为0时表示不存在
int maxdepth,n; //树的最大深度,树的结点数
int depth[N];//各结点在树上的深度
void init(){ //预处理函数
for(int k=0;1<<k<=maxdepth;k++) //初始化根节点1的父亲结点全为空
fa[1][k]=0;
for(int k=1;1<<k<=maxdepth;k++)//倍增跳的深度2^k
for(int i=2;i<=n;i++) //对每个结点都预处理
fa[i][k]=fa[fa[i][k-1]][k-1]; //当前结点的2^k父亲就是当前结点的2^(k-1)的2^(k-1)父亲结点
//在计算2^k父亲结点之前所有的2^(k-1)父亲结点都已算出
}
2:查询部分(查询x和y的LCA):首先让更深的y跳到与x同样的深度,此处跳的长度是两者深度差以内的最大的2的某次幂。然后x和y在同样的深度一起往上跳,跳的深度也是2的尽可能大的某次幂
复杂度O(logn)
eg:x和y深度差de=11,先跳8,再跳2,再跳1,二者便在同一深度,类似于快速幂(1011)。
int find(int x,int y){
if(depth[x]>depth[y]) swap(x,y); //令y为更深
while(depth[y]>depth[x]) //当不是同一深度时
y=fa[y][int(log(depth[y]-depth[x])/log(2))]; //让y尽可能的往上跳
//跳到2^a父亲结点中去,a=以2为底深度差的对数(的整数部分)
if(x==y) return x;//此时恰巧重合
for(int k=log(depth[x])/log(2);k>=0;k--) //从最大跨度开始跳
if(fa[x][k]!=fa[y][k]) //fa[x][k]==fa[y][k],是公共祖先但不一定是最近公共祖先
x=fa[x][k],y=fa[y][k]; //二者同时往上尽可能的跳
//这个for循环不会到达最近公共祖先,而是到达最近公共祖先的孩子结点
return fa[x][0];//输出上面最后的孩子结点的父亲结点
}
模板题:
洛谷P3379最近公共祖先(LCA)
题目描述:
给定一棵有根多叉树,请求指定两个点直接最近公共祖先。
输入格式:
第一行包含三个正整数N,M,S(N,M<=500000),分别表示树的结点个数、询问的个数和树根结点的序号。
接下来N-1行每行包含两个正整数x,y,表示x结点和y结点之间有一条直线连接的边(数据保证可以构成树)
接下里M行每行包含两个正整数a,b,表示询问a结点和b结点的最近公共祖先
输出格式:
输出包含M行,每行包含一个正整数,依次为每一个的询问结果
输入样例: 输出样例:
5 5 4 4
3 1 4
2 4 1
5 1 4
1 4 4
2 4
3 2
3 5
1 2
4 5
模板代码:
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
using namespace std;
const int N=500005;
const int dep=20;
int fa[N][dep];
int depth[N]={0};
vector<int>e[N];
int n,m,s;
int maxdepth=0;
void dfs(int x,int y){ //dfs遍历无向图,确定各个结点的深度(depth[]),树的深度(maxdepth),父亲结点(fa[i][0])
for(int i=0;i<e[x].size();i++){
if(e[x][i]==y) continue;
depth[e[x][i]]=depth[x]+1;
maxdepth=max(maxdepth,depth[e[x][i]]);
fa[e[x][i]][0]=x;//一倍父亲结点
dfs(e[x][i],x);
}
}
void init(int x){//初始化倍增结点(fa[x][i])
for(int i=0;i<dep;i++) fa[x][i]=0;//为0表示不存在2^k倍父亲结点
for(int i=1;(1<<i)<=maxdepth;i++){
for(int j=1;j<=n;j++){
if(j==x) continue;
fa[j][i]=fa[fa[j][i-1]][i-1];
}
}
}
int find(int x,int y){//查找结点x,y的最近公共祖先
if(depth[x]>depth[y]) swap(x,y);
while(depth[y]>depth[x])
y=fa[y][int(log(depth[y]-depth[x])/log(2))];
if(x==y) return x;
for(int i=(log(depth[y])/log(2));i>=0;i--)
if(fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
int main(){
cin>>n>>m>>s;
int u,v;
for(int i=1;i<n;i++){
cin>>u>>v;
e[u].push_back(v);//构造无向图
e[v].push_back(u);
}
depth[s]=0;//初始根节点深度为0
dfs(s,-1);
init(s);
while(m--){
cin>>u>>v;
cout<<find(u,v)<<endl;
}
return 0;
}
注:不过这个代码有两个点过不去,即便使用链式前向星(听说比vetor快)但仍旧有两个点过不去(超时),下面的Tarjan倒是可以(⊙﹏⊙)
链式前向星:
#include<bits/stdc++.h>
using namespace std;
const int N=500005;
int maxdepth=0;
int fa[N][20],depth[N];
int LCANum=0,LCATo[2*N],LCANext[2*N],LCAHead[N]={0};
inline void AddEdge(int u,int v){
LCATo[++LCANum]=v,LCANext[LCANum]=LCAHead[u],LCAHead[u]=LCANum;
}
inline void dfs(int x,int y){
for(int e=LCAHead[x];e;e=LCANext[e]){
if(LCATo[e]==y) continue;
fa[LCATo[e]][0]=x;
depth[LCATo[e]]=depth[x]+1;
if(depth[LCATo[e]]>maxdepth) maxdepth=depth[LCATo[e]];
dfs(LCATo[e],x);
}
}
inline void init(int x,int n){
for(int i=0;i<20;i++) fa[x][i]=0;
for(int i=1;(1<<i)<=maxdepth;i++){
for(int j=1;j<=n;j++){
if(j==x) continue;
fa[j][i]=fa[fa[j][i-1]][i-1];
}
}
}
inline int find(int x,int y){
if(depth[x]>depth[y]) swap(x,y);
while(depth[y]>depth[x]){
y=fa[y][int(log(depth[y]-depth[x])/log(2))];
}
if(x==y) return x;
for(int i=log(depth[y])/log(2);i>=0;i--){
if(fa[x][i]!=fa[y][i]){
x=fa[x][i];
y=fa[y][i];
}
}
return fa[x][0];
}
int main(){
int n,m,s;
cin>>n>>m>>s;
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
AddEdge(u,v);
AddEdge(v,u);
}
depth[s]=0;
dfs(s,-1);
init(s,n);
int u,v,x;
while(m--){
scanf("%d%d",&u,&v);
x=find(u,v);
cout<<x<<endl;
}
}
洛谷P1967货车运输
题目描述:
A国有n座城市,编号从1到n,城市之间有m条双向道路,每一条道路对车辆都有重量限制,简称限重。现在又q辆货车在此运输货物,司机们想知道,每辆车在不超过车辆限重的情况下。最多可以运多重的货物。
输入格式:
第一行有两个用一个空格隔开的整数n,m(n<=10000,m<=50000),表示A国有n座城市和m条道路。接下来m行,每行三个整数x,y,z,每两个整数之间用一个空格隔开,表示在x城市和y城市之间存在一条限重为z(z<=100000)的道路。
注意:x!=y,两座城市之间可能有多条道路。
接下一行有一个整数q(q<=30000),表示有q辆货车需要运输。
接下来q行,每行两个整数,之间用一个空格隔开,表示一辆货车需要从x城市到y城市,保证x!=y
输出格式:
共有q行,,每行一个整数,表示对于每一辆货车,它的最大载重是多少。
如果货车不能到达目的地,输出-1
题解:(最小值的最大化问题)
求出两点之间路径(若干条路径)上最小边权的最大值。
给定两点之间可能会有多个路径,由于要求的是路径上的边权的最小值,这个最小值要最大,因此可以先用最大生成树算法生成一个边权尽可能大的连通图,这样路径就是唯一的,要求的答案就是这个路径上的最小边权,此处可以使用倍增LCA算法中的思想来实现,两结点之间的简单路径就是先到他们的LCA,再到另一个结点。
AC代码:
#include<iostream>
#include<queue>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=10005;
int n,m,q;
int depth[N];//结点的深度
int fa[N][16];//倍增父亲结点
int min_edge[N][16]={0}; //与倍增父亲结点之间的最小值
struct node{
int x,y,z;
}b;//表示输入的边
struct edg{
int x,z;
}d;//表示放入图中的边
vector<struct edg>e[N];//无向图的边的存储
vector<int>se[N];//se[i]存储表示以i为根节点的树的结点编号的集合 ,包括根节点本身
int c[N];//并查集的标记数组
int find_bing(int x){
if(c[x]==x) return x;
return c[x]=find_bing(c[x]);
}
void merge(int x,int y){
int fx=find_bing(x),fy=find_bing(y);
c[fx]=fy;
}
void dfs(int x,int y){
for(int i=0;i<e[x].size();i++){
d=e[x][i];
if(d.x==y) continue;
depth[d.x]=depth[x]+1;
fa[d.x][0]=x;
min_edge[d.x][0]=d.z;
dfs(d.x,x);
}
}
void init(int x){
for(int i=0;i<16;i++) fa[x][i]=0;
for(int i=1;i<16;i++){
for(int j=0;j<se[x].size();j++){
if(se[x][j]==x) continue;
int y=se[x][j],fy=fa[y][i-1];
min_edge[y][i]=min(min_edge[y][i-1],min_edge[fy][i-1]);
fa[y][i]=fa[fy][i-1];
}
}
}
int find(int x,int y){
int minn=100000000;
if(depth[x]>depth[y]) swap(x,y);
while(depth[y]>depth[x]){
minn=min(minn,min_edge[y][int(log(depth[y]-depth[x])/log(2))]);//这步之前与下行代码位置错了,醉了
y=fa[y][int(log(depth[y]-depth[x])/log(2))];
}
if(x==y) return minn;
for(int i=log(depth[y])/log(2);i>=0;i--){
if(fa[x][i]!=fa[y][i]){
minn=min(minn,min_edge[x][i]);
minn=min(minn,min_edge[y][i]);
x=fa[x][i],y=fa[y][i];//这里与上面两行的顺序之前又错了,,,,,,
}
}
minn=min(minn,min_edge[x][0]);
minn=min(minn,min_edge[y][0]);
return minn;
}
bool operator<(struct node a,struct node b){
return a.z<b.z;
}//队首元素大
int main(){
cin>>n>>m;
priority_queue<struct node,vector<struct node> ,less<struct node> >que;
while(m--){
cin>>b.x>>b.y>>b.z;
que.push(b);
}
int s=0;
for(int i=1;i<=n;i++) c[i]=i;
while(s<n-1&&!que.empty()){//当找到n-1条边,或者所有的边都遍历完
b=que.top();
que.pop();
if(find_bing(b.x)==find_bing(b.y)) continue;
merge(b.x,b.y);
d.x=b.y,d.z=b.z;
e[b.x].push_back(d);
d.x=b.x;
e[b.y].push_back(d);
s++;
}
for(int i=1;i<=n;i++){
se[find_bing(i)].push_back(i);
}
for(int i=1;i<=n;i++){
if(c[i]==i) {
depth[i]=0;
dfs(i,-1);
init(i);
}
}
int u,v;
cin>>q;
while(q--){
cin>>u>>v;
int w;
if(find_bing(u)!=find_bing(v)) w=-1;
else w=find(u,v);
cout<<w<<endl;
}
return 0;
}
注:在求倍增节点的过程中,可以顺便求出类似最小最大权值,权值和等信息。
方法三:Tarjan算法求LCA
复杂度:O(n+q)比倍增算法快
原理:离线(要先知道所有的询问)(也就是直接一遍求出所有需要查询结点的LCA)处理询问,将询问用链表存在相关的结点上,dfs遍历整棵树,当到x结点发现y结点已经到过了时,此时y结点上方还未回溯的结点就是(x结点和y结点)的LCA。

洛谷P3379最近公共祖先(LCA)
#include<bits/stdc++.h>
using namespace std;
const int N=500005;
int LCAUFS[N];
int Is_Pass[N]={0};
int ans[N];
int LCANum=0,LCATo[2*N],LCANext[2*N],LCAHead[N]={0};//注意这里与下一行中好几个数组开的是2*N空间,是因为要存两遍
int QueryNum=0,QueryTo[2*N],QueryNext[2*N],QueryHead[N]={0},Pos[2*N];
/*int UFSFind(int x){
if(x==LCAUFS[x]) return x;
return LCAUFS[x]=UFSFind(LCAUFS[x]);
}*/
int UFSFind(int x){//非递归路径压缩并查集比递归压缩要快 ,当然一般情况递归就够用了
int re=x,p;
while(LCAUFS[re]!=re) re=LCAUFS[re];
while(LCAUFS[x]!=x) p=x,x=LCAUFS[x],LCAUFS[p]=re;
return re;
}
void AddLCAEdge(int u,int v){
LCATo[++LCANum]=v,LCANext[LCANum]=LCAHead[u],LCAHead[u]=LCANum;
}
void AddQueryEdge(int u,int v,int num){
QueryTo[++QueryNum]=v,QueryNext[QueryNum]=QueryHead[u],QueryHead[u]=QueryNum,Pos[QueryNum]=num;//Pos存储的是第i组数据是在输入的第num组数据
}
void Tarjan(int x,int y){
LCAUFS[x]=x;//使用并查集表示x所在回溯树的根节点,也就是结点上方还未回溯的结点(也就是最近LCA)
Is_Pass[x]=1;//标记x结点已经到过了,但不一定进行了回溯
for(int e=LCAHead[x];e;e=LCANext[e]){//递归遍历其子结点
if(LCATo[e]==y) continue;
Tarjan(LCATo[e],x);
LCAUFS[LCATo[e]]=x;
//表示此时已经是到了LCATo[e]结点的回溯时刻,需要利用并查集的知识
//来标记该结点回溯树的根节点,此时表示刚回溯到此结点时,其所在回溯树
//的根结点是其父亲结点
}
//需要知道回溯的过程一定是先回溯子结点之后才能回溯祖先结点
for(int e=QueryHead[x];e;e=QueryNext[e]){//表示e结点已经经过了并且现在是正在回溯的过程中
if(Is_Pass[QueryTo[e]]){//只要与其对应的结点已经经过就可以
ans[Pos[e]]=UFSFind(QueryTo[e]);
}
}
return ;
}
int main(){
int n,m,s;
cin>>n>>m>>s;
for(int i=1,u,v;i<n;i++){
scanf("%d%d",&u,&v);
//使用链式前向星存储树的边
AddLCAEdge(u,v);
AddLCAEdge(v,u);
}
for(int i=1,u,v;i<=m;i++){
scanf("%d%d",&u,&v);
//使用链式前向星存储每个结点与哪几个结点进行求LCA
AddQueryEdge(u,v,i);
AddQueryEdge(v,u,i);
}
Tarjan(s,-1);
for(int i=1;i<=m;i++)
printf("%d\n",ans[i]);
return 0;
}
注:前面不少地方使用了链式前向星。所谓的链式前向星就是vector<int>e[N]方法存储图的边的另一种方法,而且比vector方法快。可以理解使用数组(使用结构体的话可能会更容易理解)完成的邻接表(指针完成的邻接表比较复杂,而且带有指针,比较容易出错)。每次操作就是在邻接表的最前面插入一个元素,与指针类型的邻接表其实在本质上没有什么大区别。
void AddLCAEdge(int u,int v){
LCATo[++LCANum]=v,LCANext[LCANum]=LCAHead[u],LCAHead[u]=LCANum;
}
虽然Tarjan算法比倍增算法快,但是在一些场合还是会使用倍增算法,因为倍增算法不仅可以求出祖先结点的信息,还可以获得权值和,最小权值,最大权值等信息