浅入理解傅里叶变换

文章首发于个人站点：隐舍 | 理解傅里叶变换

傅里叶变换

傅立叶变换是将时域的函数转换成频域上的函数，是对于同一个函数的不同视角。数学定义如下：
$F(w)=F(f(t))=\int{f(t)e^{-iwt}}dt$

笛卡尔坐标系中的变换

对着数学公式来理解傅里叶变换确实有点难度,下面先从笛卡尔坐标系了解什么是变换。

上图为一个简单的二维笛卡尔坐标系，从图中我们可以看出A点坐标为(-3,1),B点坐标为(2,3),那么为什么可以这样表示呢？

这是由于笛卡尔坐标系中定义了一组标准正交基 $e_x=(1, 0)$和 $e_y=(0,1)$，（PS：基是向量，正交基指不同基的内积为0，标准基指基的模为1）

以点D为中心那么点A的位置可以表示为 $-3e_x+e_y$，点B的位置可以表示为 $2e_x+3e_y$，从式中可以看出点的坐标是由基前面的系数表示的。

上面笛卡从尔坐标系中点的坐标表示也是一种变换，将图中顶点变换到坐标系中表示。傅里叶变换只是相对更加复杂的变换而已！

傅里叶级数

傅里叶变换包括傅里叶级数和连续傅里叶变换，下面先讨论傅里叶级数。

傅立叶级数适用于周期性函数，可以将任何周期性函数分解成简单震荡函数的集合（正弦函数和余弦函数），如下图所示：

上图左侧是一个周期函数，右侧是将周期函数分解成多个简单震荡函数，这个周期函数用数学公式可以表达为：
$f(t) \approx 2.5+\frac{10}{\pi}\left(\sin \frac{\pi t}{4}+\frac{1}{3} \sin \frac{3 \pi t}{4}+\frac{1}{5} \sin \frac{5 \pi t}{4}+\frac{1}{7} \sin \frac{7 \pi t}{4}\right)$
图中左侧的信号是随着时间而变化的，称为时域（time domain）。

根据右侧分解的多个简单震荡函数可知，不同的震荡函数有不同的振幅和频率。以第一个波形为例，振幅 $A=1$，频率 $f=w/2\pi=1/8$。如何以频率为横坐标，振幅为纵坐标那么可以表示为下图：

图中所示信号随频率而变化的，称为频域（frequency domain）。

上述两图中以时域和频域所表示的信号是等价的，只是从不同角度来看。用一张动态图来看一下不同角度下的效果：

先来看一下傅里叶级数的公式：
$\begin{aligned} f(t) &=\frac{a_{0}}{2}+a_{1} \cos (\omega t)+b_{1} \sin (\omega t) \\ &+a_{2} \cos (2 \omega t)+b_{2} \sin (2 \omega t) \\ &+\ldots \\ &=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos (n \omega t)+b_{n} \sin (n \omega t)\right] \end{aligned}$
其中，
$\begin{aligned} a_{n} &=\frac{2}{T} \int_{t_{0}}^{t_{0}+T} f(t) \cos (n \omega t) d t \\ b_{n} &=\frac{2}{T} \int_{t_{0}}^{t_{0}+T} f(t) \sin (n \omega t) d t \end{aligned}$
详细傅里叶级数推到过程参考：傅里叶级数的推导

从时域信号 $f(t)$公式中可以看出，标准正交基为 $\{1, \sin (n \omega t), \cos (n \omega t) | n=1, \dots, \infty\}$, 对应的系数 $\left\{\frac{a_{0}}{2}, a_{n}, b_{n} | n=1, \dots, \infty\right\}$为傅里叶级数在这组标准正交基上的向量。（PS：可自行证明该组基为正交基。）

这就是傅里叶变换，将时域信号变换到频域当中。

傅里叶变换

傅里叶级数是针对周期性函数的，但是现实中大多数函数都是非周期性的。那么如何处理非周期性的函数呢？

傅立叶变换，是傅立叶级数的推广。

首先需要先了解下欧拉公式，详细推导过程参考：怎么向小学生解释欧拉公式 e^(πi)+1=0

考虑横轴为1，纵轴为虚数 $i$, 那么空间中的点可以表示为 $\cos \theta+i \sin \theta$。

根据欧拉公式上式可以推导为：
$\cos \theta+i \sin \theta=e^{i \theta}$
那么坐标系中的点有两种表示形式：

考虑到角大小 $\theta=\omega t$， $\theta$会随着 $t$ 的增大而逆时针旋转，因此 $e^{i\omega t}$可以表示点A随着 $t$的变化而逆时针旋转。如果 $\omega$ 取不同大小的值，对应的虚轴的运动轨迹则不同，如下图所示:

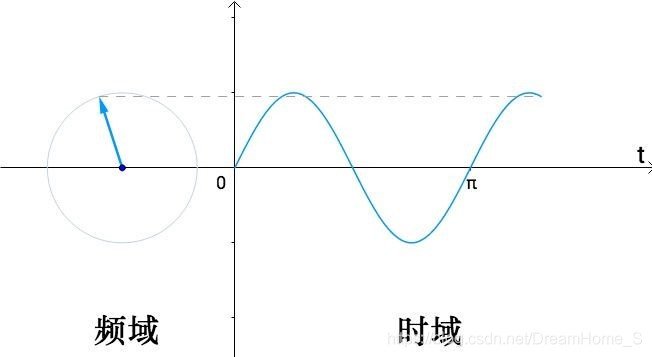
左侧图是旋转频率，称为频域；右侧图是随时间变化的幅度，称为时域；那么上图就展示了频域转化到时域的过程。

以上简单阐述了欧拉公式及其表示，接着解释傅里叶变换如何处理非周期函数。

将非周期函数考虑为周期无穷大的函数，考虑频域中的横坐标： $f=\frac{1}{T}$，当周期 $T$ 趋于无穷大时，频域图就从离散点变为连续的曲线，如下图：

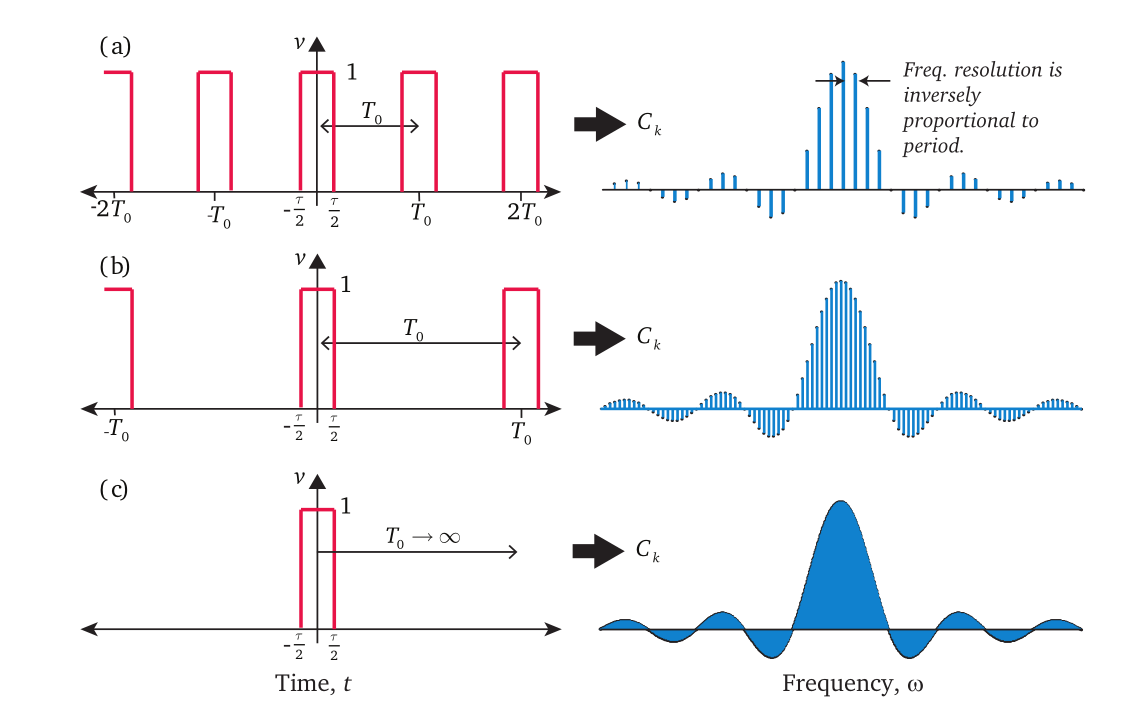
• (a). 周期函数，可以通过傅立叶级数画出频域图
• (b). 增长周期，频域图变得越来越密集
• ©. $T\rightarrow \infty$得到傅立叶变换，频域图变为连续的曲线

如何从非周期函数中分解出各种信号呢？两种解释：

• 利用正交基相乘为0

  比如说，假设这函数中有一个 $cos(n\omega x)$ 的信号，可以用 $cos(n\omega x)$把它乘出来，而其他分量如 $\{1, \sin (m \omega x), \cos (k \omega x) | m, k=[1 \ldots \infty), k \neq n\}$ 都是正交基相乘为0得到频域信号。

  对时域函数做一个内积：
  $\mathcal{F}_{T}(\omega)=\int_{-\infty}^{+\infty} f(t) e^{-i \omega t} d t$

  式中， $e^{-i \omega t}$是一组正交基的组合，复数 $i$含义：实数部分表示振幅，虚数部分表示相位。我们用正交基去与函数求内积，如果原函数中包含频率为 $\omega$ 的三角函数，则 $\mathcal{F}_{T}(\omega)$ 不为0，反之为 0，这样可以分离出相应的信号，其图示如上图 © 中右部分所示。

• 利用欧拉公式变换傅里叶级数：

  详细推导内容参考：从傅立叶级数到傅立叶变换

上述内容简单解释了傅里叶变换，傅里叶逆变换为：
$f(t)=\frac{1}{2 \pi} \int_{-\infty}^{+\infty} \mathcal{F}_{T} e^{i \omega t} d \omega$

下面两者称为傅立叶变换对，可以相互转换（时域信号和频域信号相互转换）：
$f(x) \Longleftrightarrow F(\omega)$
同一个数学对象的两种形式，一个是函数，一个是向量。

关注作者