前情提要
- 离散傅里叶变换公式
X ^ ( k N ) = ∑ n = 0 N − 1 x ( n ) e − i 2 π k N n , k = 0 , 1 , 2 , . . . , N − 1 \hat{X} (\frac{k}{N}) = \sum_{n=0}^{N-1} x(n) e^{-i2 \pi \frac{k}{N}n},k=0,1,2,...,N-1 X^(Nk)=n=0∑N−1x(n)e−i2πNkn,k=0,1,2,...,N−1 - 离散傅里叶逆变换公式
x ( n ) = 1 N ∑ k = 0 N − 1 X ^ ( k N ) e i 2 π k N n x(n) = \frac{1}{N} \sum_{k=0}^{N-1} \hat{X} (\frac{k}{N}) e^{i2 \pi \frac{k}{N}n} x(n)=N1k=0∑N−1X^(Nk)ei2πNkn
为什么需要短时傅里叶分析
离散傅里叶分析是对一段有限时间非周期离散信号(设采样频率为sr,采样点个数为N)的分解,通过对整段原始信号应用离散傅里叶变换公式,得到有限频率范围内,每个频率对应的最佳振幅和初相。频率范围为: { 0 , 1 N s r , 2 N s r , . . . , N − 1 N s r } \left \{ 0, \frac{1}{N} s_r, \frac{2}{N} s_r,...,\frac{N-1}{N} s_r \right \} { 0,N1sr,N2sr,...,NN−1sr}。
这里的“最佳”指:由该频率、振幅和初相决定的正弦信号,在该频率下,与原始信号的相似度最高。
显然,离散傅里叶分析是对原始信号的全局分析,但在音频信号处理领域,需要对更细小的时间间隔进行分析,并且最终得到原始信号的时频谱图(spectrogram)。
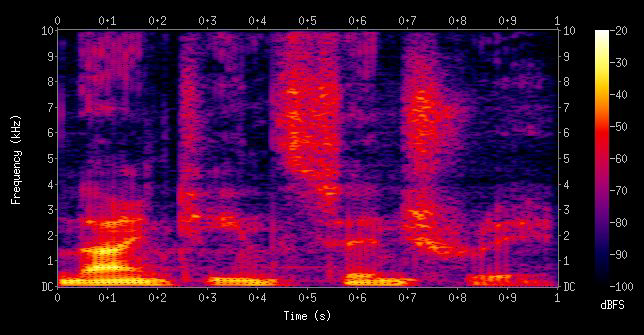
时频谱图包含了原始信号在各个细小的时间间隔(横坐标)内的频率(纵坐标)以及功率(背景颜色,通常用振幅的平方表示)的信息,要绘制时频谱图,需要短时傅里叶变换(Short-Time Fourier Transformation,STFT)。
短时傅里叶变换
短时傅里叶变换包括:分帧->加窗->离散傅里叶变换。
-
分帧:用一个窗口,沿着原始信号的时间轴滑动,有窗口大小——frame-size,和步长——hop-size两个参数,这两个参数的单位通常是整数个采样点。
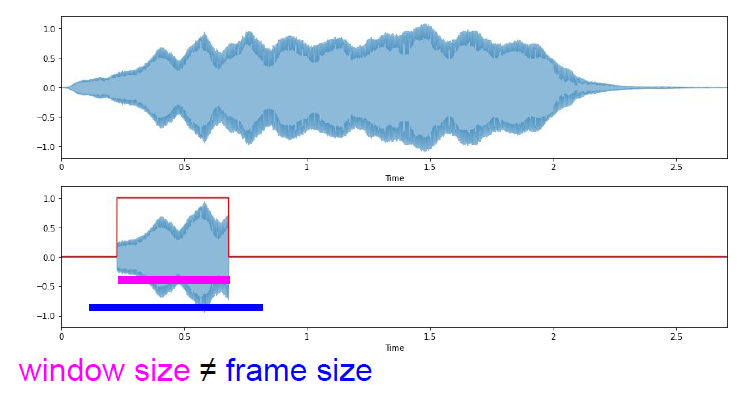
有时会有window-size这个参数,通常情况下window-size是等于frame-size的。
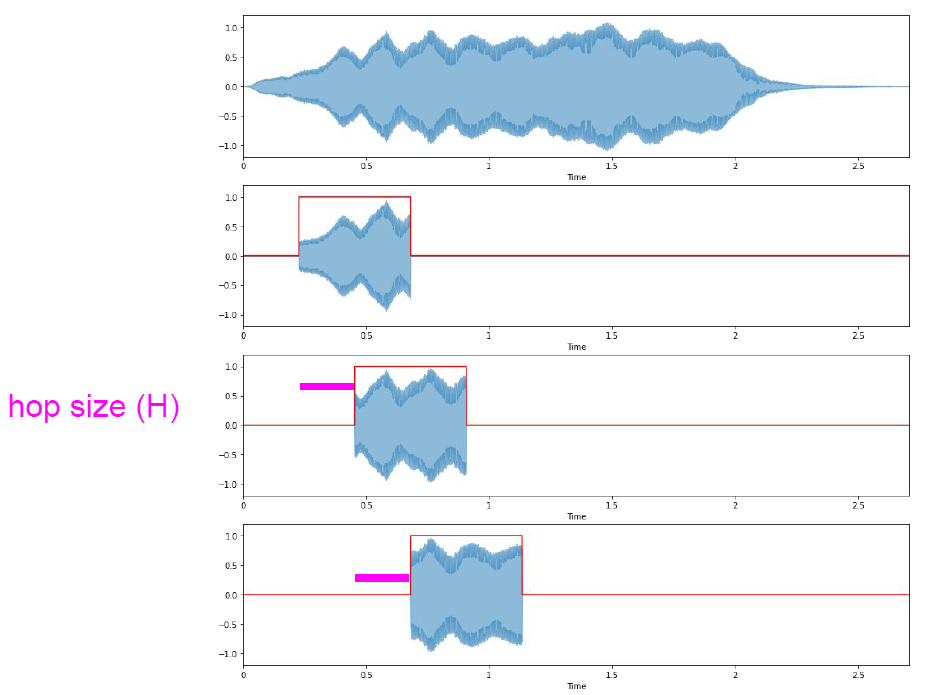
hop-size小于frame-size时,会出现frame之间的重叠,这个重叠是必要的,原因之后讲。 -
加窗:使用窗函数,对一个帧内的所有采样点加权,窗函数通常有高斯窗、汉明窗和汉宁窗。后两者是用的最多的,可以统一表示为:
w [ n ] = ( 1 − α ) − α c o s ( 2 π n N − 1 ) w[n] = (1-\alpha)-\alpha cos(\frac{2 \pi n}{N-1} ) w[n]=(1−α)−αcos(N−12πn)
当 α = 0.5 \alpha=0.5 α=0.5 时,上述为汉宁窗;当 α = 0.46 \alpha=0.46 α=0.46 时,上述为汉明窗。这三种窗函数都是“钟”形的。下图为汉宁窗,特点是过零点。

窗函数的大小由window-size指定,librosa中如果不指定window-size,则window-size = frame-size,本文也约定这两者是相等的,因此N = frame-size = window-size。 -
短时傅里叶变换:公式如下
S ( m , k ) = ∑ n = 1 N − 1 x ( n + m H ) w ( n ) e − i 2 π k N n S(m,k) = \sum_{n=1}^{N-1} x(n+mH)w(n)e^{-i2 \pi \frac{k}{N} n} S(m,k)=n=1∑N−1x(n+mH)w(n)e−i2πNkn
再次强调,式子中的N = frame-size = window-size,m是当前窗口的序号,第一个窗口序号为0,H = hop-size,w(n)是窗函数。当前窗口的左侧坐标就是mH,因此要取原始信号在n+mH处的值,进行傅里叶变换。
fft需要在2的整数次幂的采样点上才能工作,所以对于不是2的整数次幂的frame-size,会在frame的两边填充上0,比如说frame-size = 400,则会两边各填充56个0,达到512。因为经过窗函数处理后,帧两边的值也接近0,所以不会导致不连续。 -
解释一下为什么要用窗函数和为什么帧之间必须要重叠:分帧时,在分帧的边界处会造成额外的不连续性,这种不连续性是原始信号所没有的,直接对存在额外不连续性的信号做傅里叶变换,会导致频谱泄漏(spectral leakage)。频谱泄漏的原因如下:
- 所处理的信号的持续时间不为整数个周期,这种情况经常出现
- 信号的结束点是不连续的,分帧就会导致这种情况
频谱泄露会导致在频谱图上,出现原始信号所不存在的高频分量,这些高频分量是从不连续点中泄漏出来的。
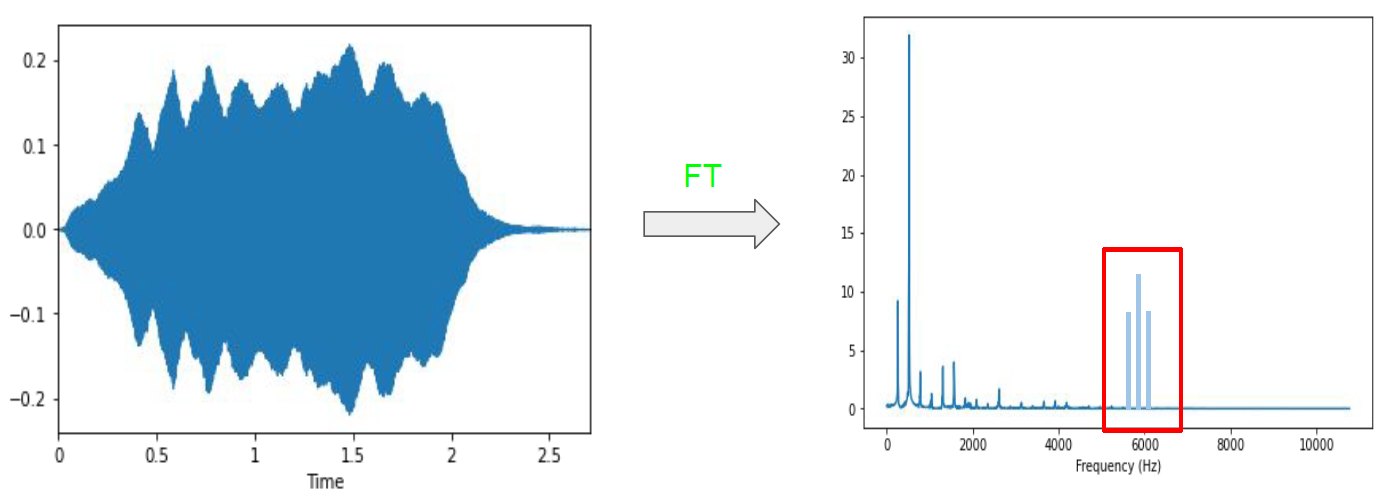
如果使用了窗函数,尤其是过零点的窗函数(如:汉宁窗),则能够从帧的两边渐进地抑制这种不连续性,效果如下:
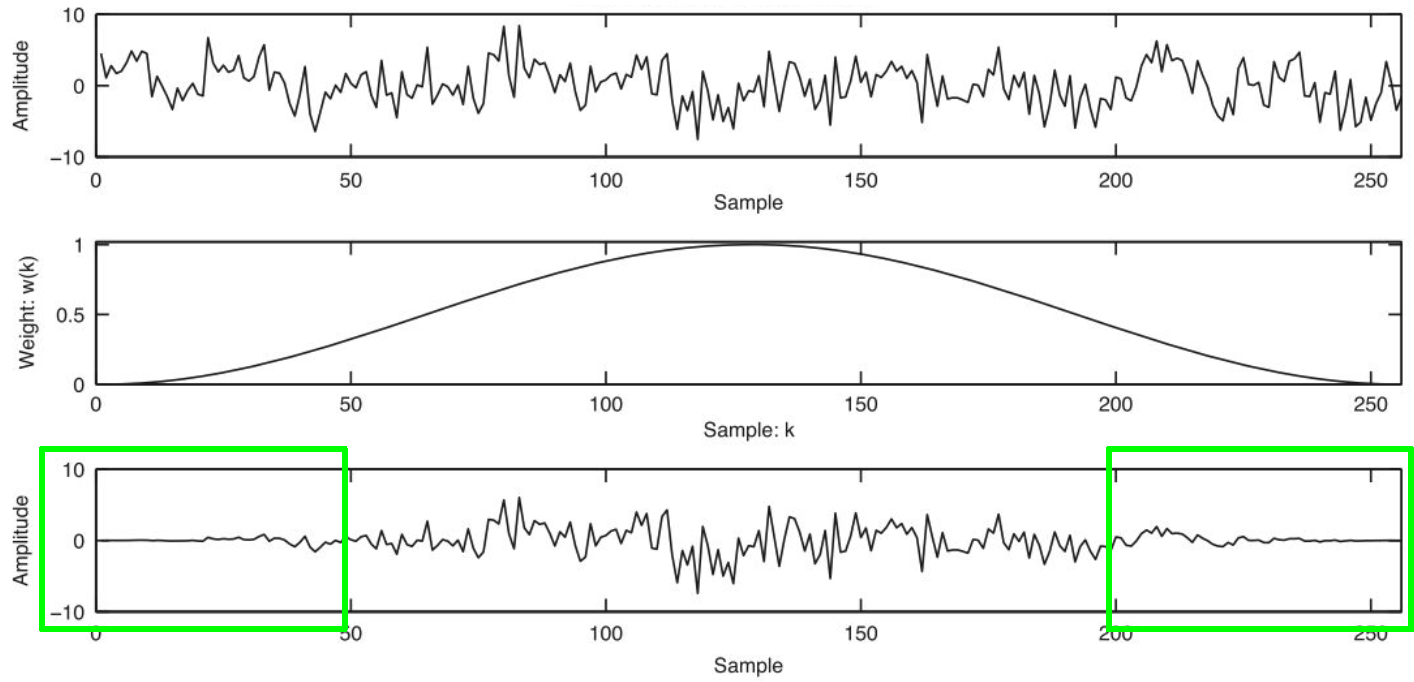
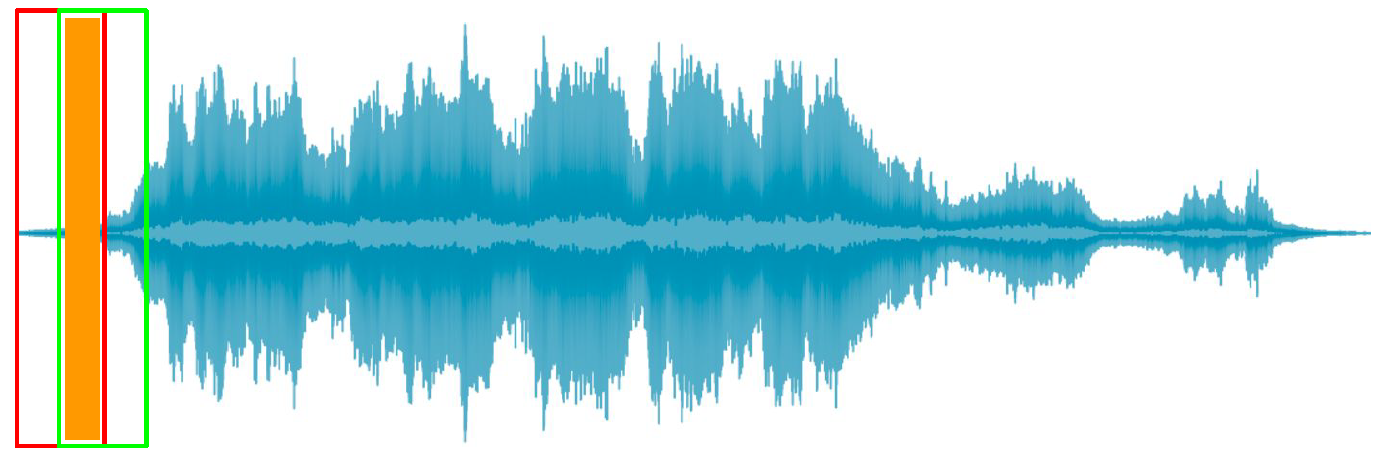
但越是对两边进行抑制,就越容易丢失两边的信息,对于不重叠的帧而言,大量信息被抑制,如下图所示:

因此帧之间的重叠是必要的,帧重叠会使每个帧都带有更多的上文信息,因此可以靠这种重叠,把被抑制的信息恢复回来。
STFT会输出什么
短时傅里叶变换会输出一个频谱矩阵,形状为[frequency-bins, frames],这两个值的计算公式如下:
f r e q u e n c y b i n s = n f f t 2 + 1 f r a m e s = s a m p l e s − f r a m e s i z e h o p s i z e + 1 \begin{aligned} frequency bins &= \frac{n_{fft}}{2} +1 \\ frames &= \frac{samples-framesize}{hopsize} +1 \end{aligned} frequencybinsframes=2nfft+1=hopsizesamples−framesize+1
-
frequency-bins要除以2是因为频谱图是以奈奎斯特频率为中心,左右对称的,原因见深入理解傅里叶变换(三)。
-
frames的计算主要考虑帧的右侧坐标,当我们放置第一个帧之后,占据frame-size个样本点,每次向右侧走一个步长hop-size个样本点,总共需要走 s a m p l e s − f r a m e s i z e h o p s i z e \frac{samples-framesize}{hopsize} hopsizesamples−framesize 步,再加上第一个放置的帧,就得到了总的帧数。
-
frame-size会影响频率分辨率(freq resolution)与时间分辨率(time resolution)。
当frame-size减小,频率分辨率会降低,虽然frequency-bins只与n-fft有关,每个frame仍然会取到奈奎斯特频率,但是frame-size减小,代表每个frame内的采样点减少了,填充了更多的0,这对恢复原始信号的频率没有帮助;同时,时间分辨率会增加,因为能得到更短时间间隔内的频谱图。
有一个不影响频率分辨率,又能提高frame数量的办法是减小hop-size。
说话人识别常用参数:采样率sr=16kHz,frame-size占据25ms,即400个采样点,可取成sr//40,hop-size占据10ms,即160个采样点,可取成sr//100,由于需要用fft,所以分帧之后,frame-size会扩充到512个采样点。
时频谱图
如果采用功率时频谱图(power spectrum),则需要求振幅的平方,下面读取了一段音频,取了前5秒,绘制时频谱图:
Y ( m , k ) = ∣ S ( m , k ) ∣ 2 Y(m,k) = |S(m,k)|^2 Y(m,k)=∣S(m,k)∣2
然后绘制热度图:
import librosa
import librosa.display
import matplotlib.pyplot as plt
def wav_to_spectrum(filepath, y_axis="linear"):
signal, sr = librosa.load(path=filepath, sr=16000)
duration = librosa.get_duration(y=signal, sr=sr)
signal = signal[:int(sr * 5)]
stft = librosa.stft(y=signal,
n_fft=512,
hop_length=sr // 100,
win_length=sr // 40)
power, phase = librosa.magphase(stft, power=2)
librosa.display.specshow(power,
sr=sr,
n_fft=512,
hop_length=sr // 100,
win_length=sr // 40,
x_axis="s",
y_axis=y_axis)
plt.colorbar(format="%+2.f")
plt.show()
if "__main__" == __name__:
debussy_path = r"16 - Extracting Spectrograms from Audio with Python\audio\debussy.wav"
wav_to_spectrum(debussy_path)
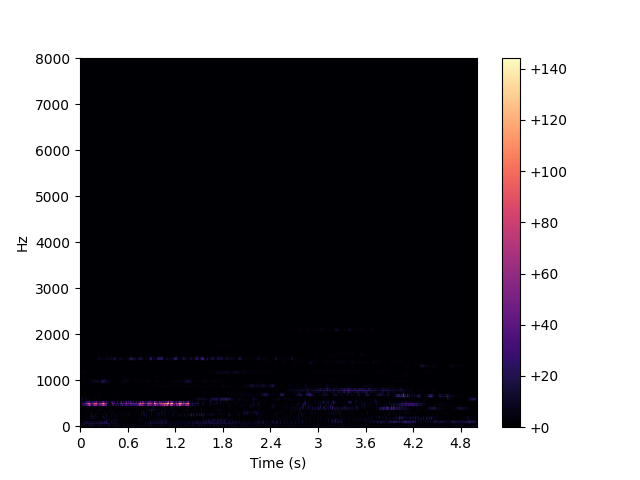
热度表示振幅的平方,是对声音强度的度量,人耳对声强的感知是非线性的,图中几乎看不出什么热度,是因为没有取分贝,取分贝实际上是一种对数运算,下式中的 P 0 P_0 P0 表示零分贝。
L d b = 10 l o g 10 ( P P 0 ) L_{db} = 10 log_{10} (\frac{P}{P_0} ) Ldb=10log10(P0P)
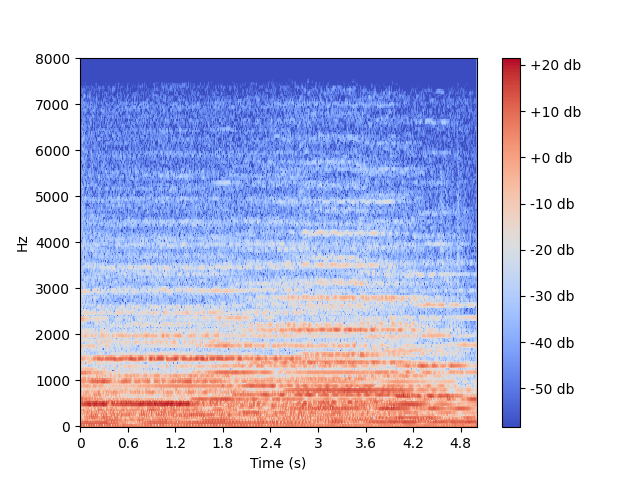
零分贝是人耳恰好能听到的最小声强,发现图中的热度大部分都是负分贝的,是因为对频率使用了“linear”线性刻度,人耳对频率的感知是非线性的,大致呈现对数形式。
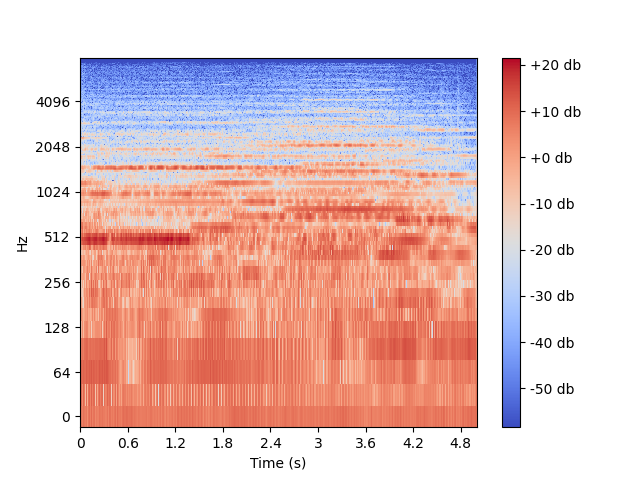
import librosa
import librosa.display
import matplotlib.pyplot as plt
def wav_to_spectrum(filepath, y_axis="linear"):
signal, sr = librosa.load(path=filepath, sr=16000)
duration = librosa.get_duration(y=signal, sr=sr)
signal = signal[:int(sr * 5)]
stft = librosa.stft(y=signal,
n_fft=512,
hop_length=sr // 100,
win_length=sr // 40)
power, phase = librosa.magphase(stft, power=2)
db = librosa.power_to_db(power)
librosa.display.specshow(db,
sr=sr,
n_fft=512,
hop_length=sr // 100,
win_length=sr // 40,
x_axis="s",
y_axis=y_axis)
plt.colorbar(format="%+2.f db")
plt.show()
if "__main__" == __name__:
debussy_path = r"16 - Extracting Spectrograms from Audio with Python\audio\debussy.wav"
wav_to_spectrum(debussy_path, "log")
其实对数频率还不够好,因为仍然有不少负分贝,而且很多高分贝部分被密集地绘制了。
深入理解傅里叶变换系列基本完结,之后的内容是与音频有关的。