本文转载于松下J27,原文分为三章讲解,在此合并转载
文一:https://blog.csdn.net/daduzimama/article/details/80109139
文二:https://blog.csdn.net/daduzimama/article/details/80394570
文三:https://blog.csdn.net/daduzimama/article/details/80394596
很多人都不了解图像(二维)频谱中的每一点究竟代表了什么,有什么意义?
一句话:二维频谱中的每一个点都是一个与之一一对应的二维正弦/余弦波。
常言道,百闻不如一见,人脑对于图像的理解能力是非常发达的。换句话说,一副图像(不论是灰度的图像还是彩色图像)所提供的信息是显而易见,清晰有力的。然而,一副图像的傅里叶频谱图,却常常让人难以理解,捉摸不透,也正因为如此,相对于一维频谱的频域处理方式而言,二维频域的处理方式显得非常有限,例如,二维卷积的频域计算,傅里叶中心切片定理Fourier Slice Theorem(医学领域)。
我这里再次选用了著名的Cameraman的图像,这幅照片向我们表达的信息是显而易见的,一位优秀的摄影师,黑色的风衣,潇洒的发型,很有质感的皮手套,灰色的裤子,一台照相机,一个三脚架,草坪,蓝天,背景是MIT。而他的频谱图则并没有像一维的频谱图那样,有助于我们理解图像自身以外的或者是隐藏在图像背后的信息。比如说,中间的那条白线是什么,如果你没看我之前写的那篇文章你可能都不知道它究竟代表了什么。这也就是我为什么说,图像的傅里叶变换有些多此一举,反而把一个简单的问题弄得很复杂,弄巧成拙了。
言归正传,说了这么多,搞图像的哪有不和二维傅里叶变换打交道的呢。现在我就尽力说明一下图像二维傅里叶变换的一些属性(这里主讲二维频谱的特性,一维里面的共有特性就不细讲了)。
1、周期性
DFT的周期性:时时刻刻都要记住,对于DFT而言,他的空域和频域始终都是沿着X和Y方向无限周期拓展的。
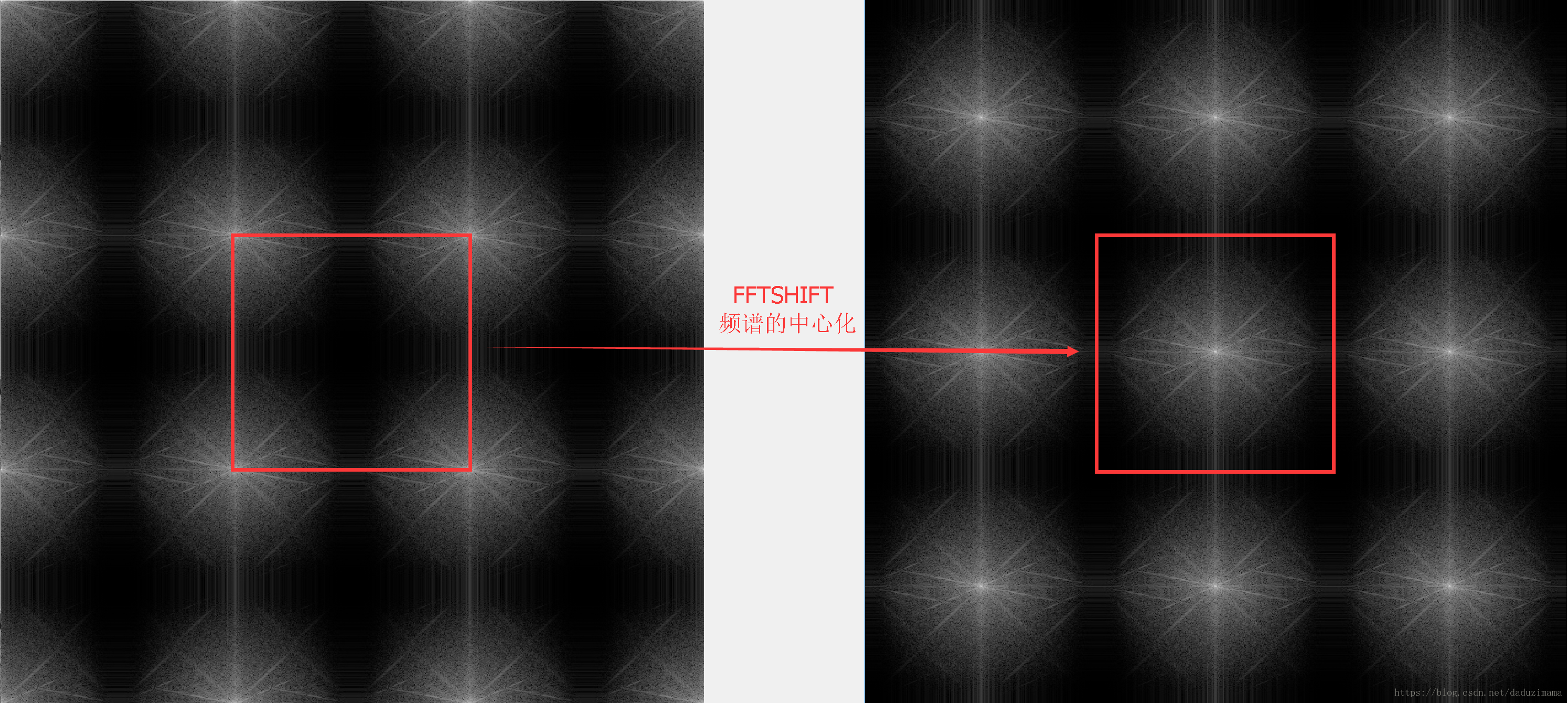
如果只取其中的一个周期,则我们会得到如下的结果(即,频谱未中心化)。
为了便于频域的滤波和频谱的分析,常常在变换之前进行频谱的中心化。
频谱的中心化
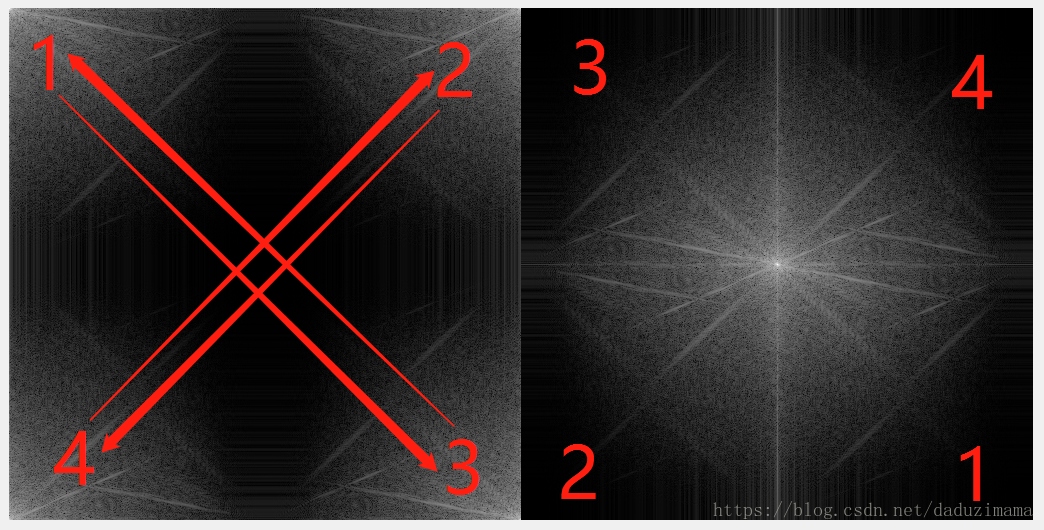
从数学上说是在变换之前用指数项乘以原始函数,又因为e^jπ = 1,所以往往我们在写程序的时候实际上是把原始矩阵乘以(-1)^(x+y)达到频谱居中的目的。如下图所示:1<—–>3 对调,2<—–>4 对调,matlab中的fftshit命令就是这么干的。
变换后对调频谱的四个象限(swap quadrant)
经过中心化后的频谱
截取了其中的一个周期,作为图像的频谱
2、高低频率的分布
除了周期性之外,还应该知道的就是哪里是高频哪里是低频。在经过频谱居中后的频谱中,中间最亮的点是最低频率,属于直流分量(DC分量)。越往边外走,频率越高。所以,频谱图中的四个角和X,Y轴的尽头都是高频。
没有经过频谱居中处理的频谱图则正好相反,中间区域是高频,而四个角则是DC低频分量。
这里我再用一个正弦波的例子来展示频谱图的高低频的分布,见下图。
频谱中心化以后,正弦波的频点靠中心越近,频率越低,离中心越远,频率越高。
3、频谱图的能量分布
这里我顺便提一下频谱中的能级分布,则如下图所示。明显,DC分量所占能量最大最多,不论是二维还是一维都应该是这样。频率越高的部分,能量越少。如下图所示,图示画的不好,勉强能够理解就好。中间最小的那个圆圈内包含了大约85%的能量,中间那个圈包含了大约93%的能量,而最外面那个圈则包含了几乎99%的能量。
4、纵横“交错”性
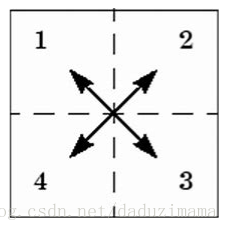
在二维傅里叶变换中,空间域中横向的周期变化会反应在频谱图中的Y轴上,而空间域中纵向的周期变化会反应在频谱图中的X轴上。空间域中东南方向的周期变化会反应在频谱图中的东北方向,反之亦然。说明见下图。
最后再附加一个例子。
5、方向性(direction)
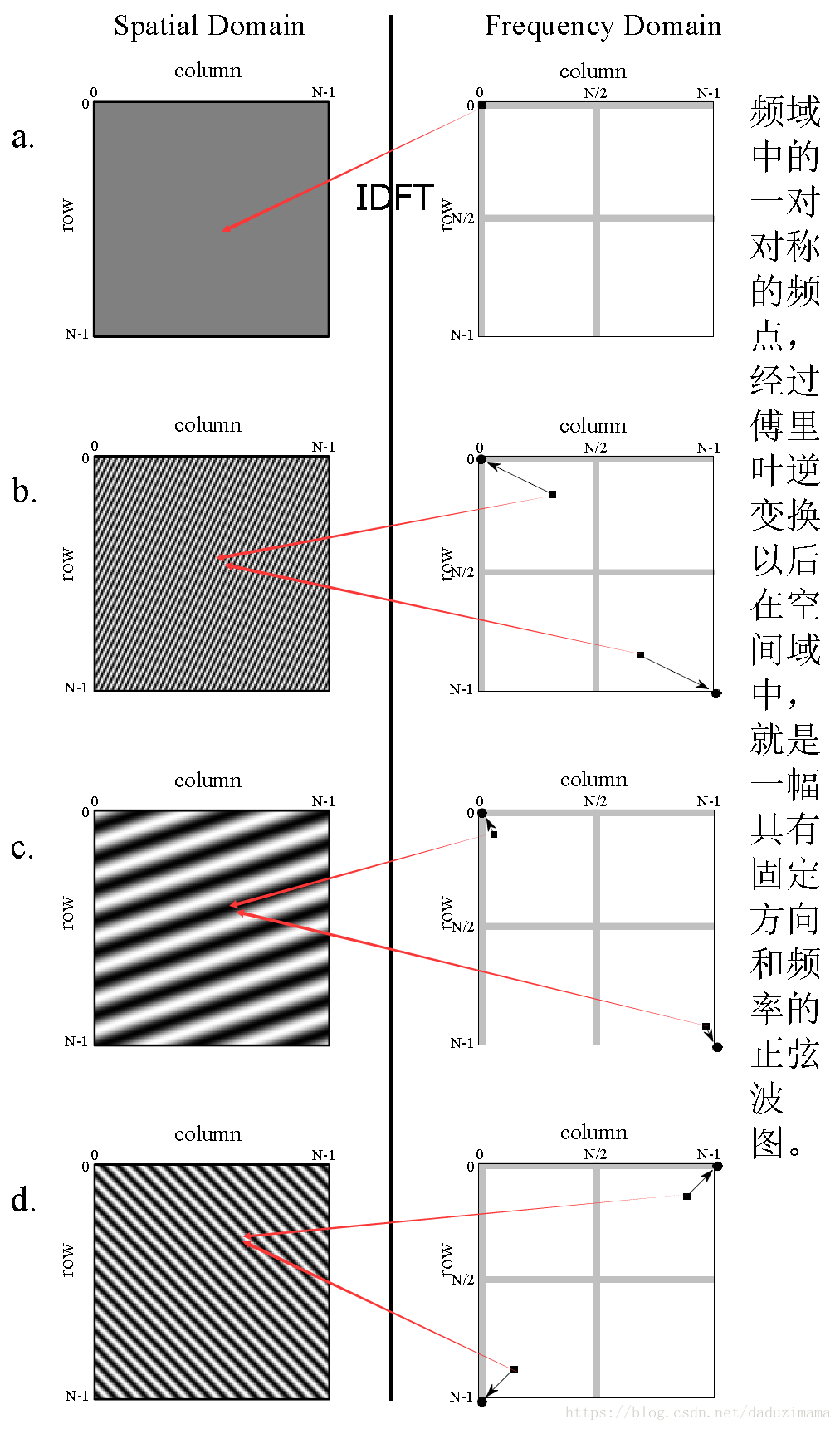
在二维频谱图中的任意“一对亮点”(注意:频谱的对称性),都在相应的空间域有一个与之相对应的二维正弦波。亮点在二维频谱中的位置决定了与之对应的正弦波的频率和方向。
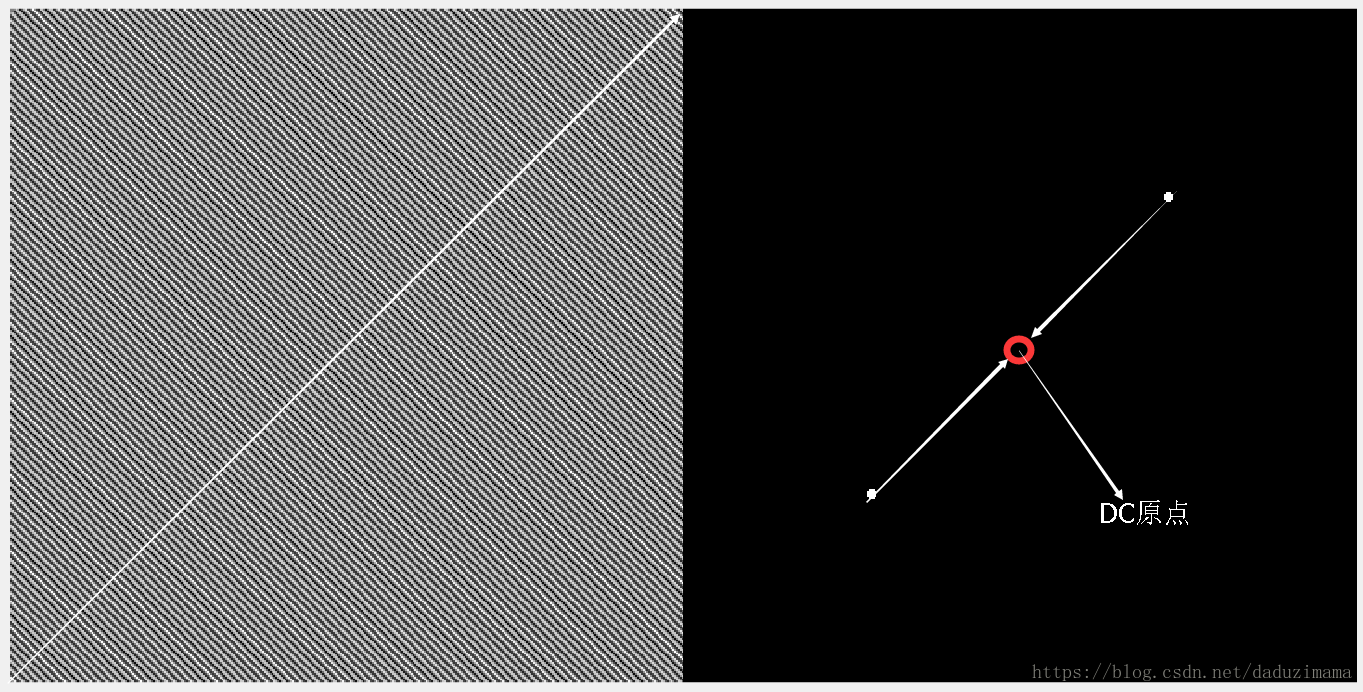
在空域图中的任意一条正弦线上,作该正弦线的法线。同时,把频谱图中的一对白色频点和坐标原点(DC中点)用一条直线连接起来。则,空域图中的法线正好和频谱图中的连线是完全平行的,一致的。
上图是一个45度倾斜的正弦波图像。
注意空间域中的任意一条法线和频谱图中频点和频谱图原点(DC)连线都是平行的,同时,空间域中的任意一条正弦线和频谱图中的连线是刚好正交的/垂直的。
上图为相同方向,较低频率正弦图的频谱。注意图中我用白色箭头所画的空间域(左图)的法线和频谱图中(右图)一对频点和DC的连线延长线,是平行的。
上图为相同方向,较高频率正弦图的频谱。注意图中我用白色箭头所画的空间域(左图)的法线和频谱图中(右图)一对频点和DC的连线延长线,是平行的。
下面我们来验证一下其他角度的情况,这一法则是否适用。
上面所有的例子中的频谱图都是频谱中心化的,那么针对没有经过频谱中心化的图呢?
这些实验还说明了一个非常重要的问题,那就是:频谱图中的任意一对对称的两点,或者说是频点,经过傅里叶反变换之后,就是空间域中的一个与之对应的正弦波(即,相应的频率和方向)。如下图所示。
6、平移和旋转
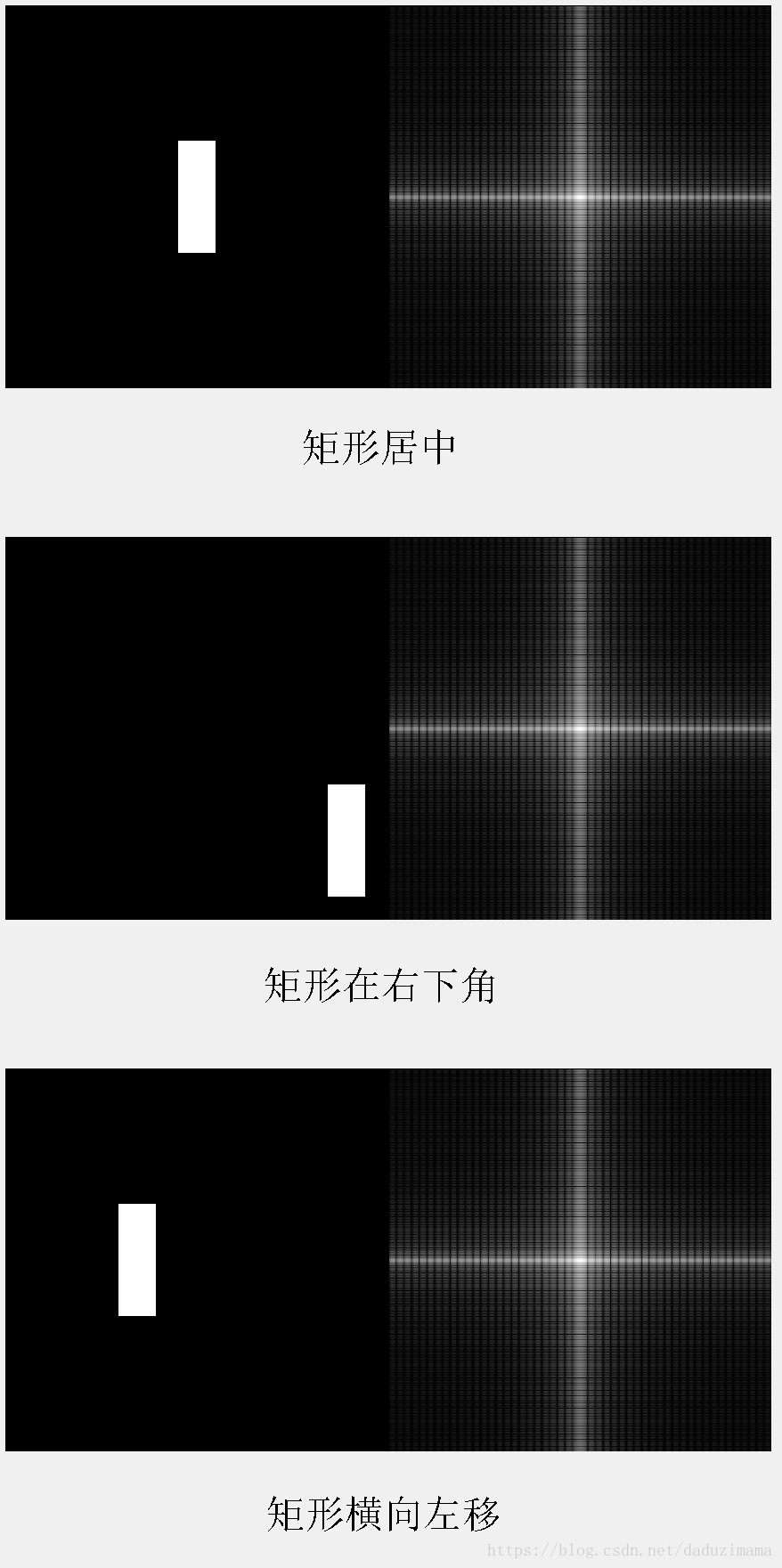
图像的平移并不会影响图像的频谱,同时,图像的相位会随着图像的旋转而旋转。
Part I 平移和旋转对频谱的影响
下面我用矩形的频谱图来说明图像中矩形的平移并不会对频谱有丝毫的影响。
再比如
再来看看频谱随着矩形的旋转而旋转相同的角度。
Part II 平移和旋转对相位的影响
先用一个简单的例子来说明图像相位的作用(所用图像为cameraman),在图像的频域分析和滤波中,相位是常常被忽略的。虽然相位分量的贡献很不直观,但是它恰恰很重要。相位是频谱中各正弦分量关于原点的位移的度量。
上面的小实验充分说明了,看似无用的,且常常被忽略的相位,在DFT的频域中起到了多么重要的作用(注意区分实部和虚部(直角坐标系)VS 频谱和相位(极坐标系)!)。
接下来我们再来看看图像在空间域中的移位和旋转对相位有什么影响。下图中,左边一列是图像,中间一列是频谱,右边一列是相位图。你必须意识到,通过肉眼,你很难从相位图中得到什么有用的信息。