深入理解傅里叶变换（二）

前情提要

寻找一个正弦波分量的公式表述如下：
$$\begin{array}{rl}{\phi }_f& =argma{x}_{\phi \in [0,1)}(\int s(t)\cdot sin[2\pi (ft-\phi )]\cdot dt)\\ d_f& =(\int s(t)\cdot sin[2\pi (ft-{\phi }_f)]\cdot dt)\end{array}$$
因此，直观来看，上述可表示为一个映射 $\hat{g}:R\to C$，输入一个实数频率，输出一个复数，这个复数包含了振幅和初相两个信息。即：
$$\begin{array}{rl}\hat{g}(f)& =c_f=\frac{d_f}{\sqrt{2}}{e}^{-i2\pi {\phi }_f}\\ {\phi }_f& =\frac{arg[\widehat{g(f)}]}{-2\pi }\\ d_f& =\sqrt{2}\cdot |\hat{g}(f)|\end{array}$$
因此，只要选定一个频率，代入计算出 $\hat{g}(f)$ 的值，即可得到对应的振幅和初相。振幅要除以根号2是某种归一化，不需要过度关注，

现在，可以给出傅里叶变换的公式了
$$\begin{array}{rl}\hat{g}(f)& =\int f(t)e^{-i2\pi ft}dt\end{array}$$

公式到底在做一件什么事

我们先制造一个信号

import matplotlib.pyplot as plt
import numpy as np


def create_signal(frequency, time: np.array):
    sin0 = np.sin(2 * np.pi * (frequency * time))
    sin1 = np.sin(2 * np.pi * (2 * frequency * time))
    sin2 = np.sin(2 * np.pi * (3 * frequency * time))

    return sin0 + sin1 + sin2

if "__main__" == __name__:
    time = np.linspace(0, 10, 1000)
    signal = create_signal(1, time=time)
    plt.plot(time, signal)

    plt.show()

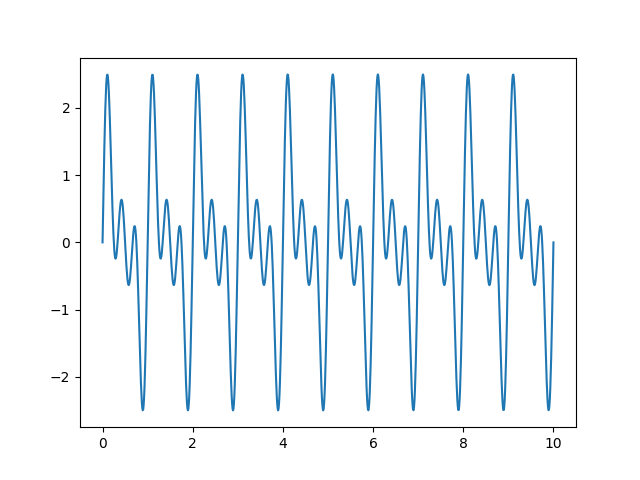
然后再制造出 $e^{-i2\pi ft}$ 这个信号，让这两个信号相乘。注意这里 $e^{-i2\pi ft}$ 信号的频率被设置为基频，相乘的结果如下：

import matplotlib.pyplot as plt
import numpy as np


def create_signal(frequency, time: np.array):
    sin0 = np.sin(2 * np.pi * (frequency * time))
    sin1 = np.sin(2 * np.pi * (2 * frequency * time))
    sin2 = np.sin(2 * np.pi * (3 * frequency * time))

    return sin0 + sin1 + sin2


def calculate_center_of_gravity(multi_signal):
    x_center = np.mean([x.real for x in multi_signal])
    y_center = np.mean([x.imag for x in multi_signal])

    return x_center, y_center


def calculate_sum(multi_signal):
    x_sum = np.sum([x.real for x in multi_signal])
    y_sum = np.sum([x.imag for x in multi_signal])

    return x_sum, y_sum


def create_pure_tone(frequency, time: np.array):
    angle = 2 * np.pi * frequency * time

    return np.cos(angle) - complex(0, 1) * np.sin(angle)


def plot_fourier_transform(signal,
                           pure_tone,
                           plot_center_of_gravity=False,
                           plot_sum=False):
    multi_signal = signal * pure_tone
    x_series = np.array([x.real for x in multi_signal])
    y_series = np.array([x.imag for x in multi_signal])

    plt.plot(x_series, y_series)

    if plot_center_of_gravity:
        center_of_gravity = calculate_center_of_gravity(multi_signal)
        plt.plot([center_of_gravity[0]], [center_of_gravity[1]],
                 marker='o',
                 markersize=10,
                 color="red")

    if plot_sum:
        integration = calculate_sum(multi_signal)
        plt.plot([integration[0]], [integration[1]],
                 marker='o',
                 markersize=10,
                 color="green")

    plt.show()


if "__main__" == __name__:
    time = np.linspace(0, 10, 1000)
    signal = create_signal(1, time=time)
    pure_tone = create_pure_tone(1, time=time)
    # plt.plot(time, pure_tone)

    # plt.show()

    plot_fourier_transform(signal,
                           pure_tone,
                           plot_center_of_gravity=False,
                           plot_sum=False)

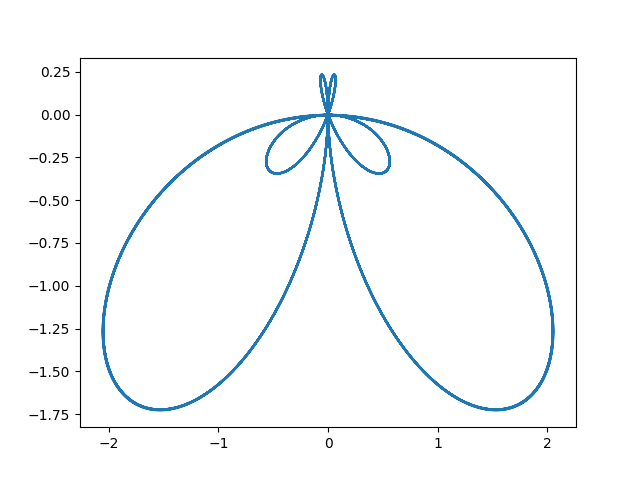
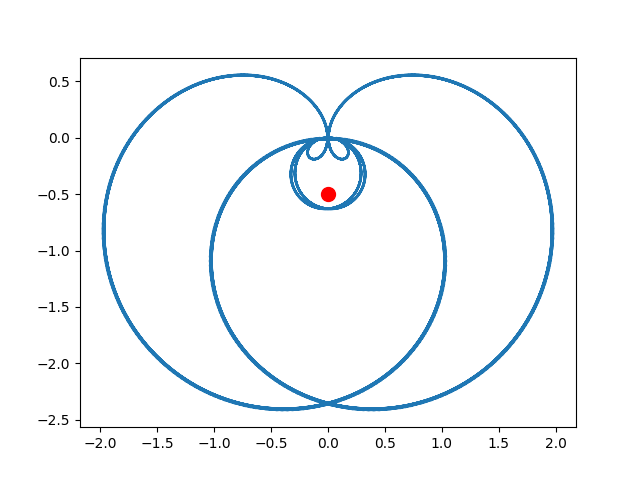
好像不是很能看出问题，如果设置 $e^{-i2\pi ft}$ 信号的频率为1.1呢，如下：

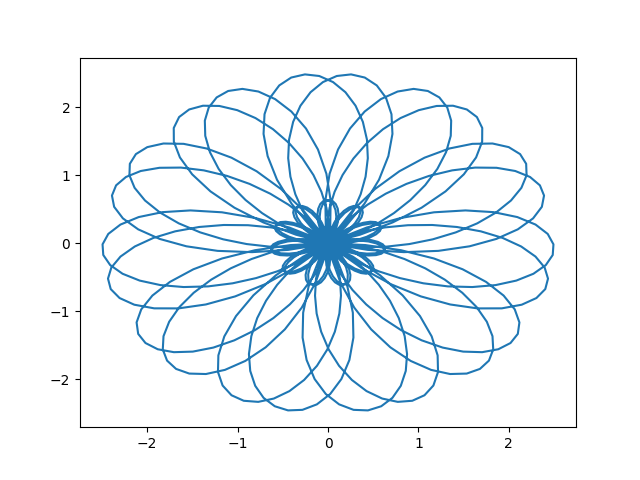
发现是对称图形，而此时如果求积分，且表示在图上，可得：

if "__main__" == __name__:
    time = np.linspace(0, 10, 1000)
    signal = create_signal(1, time=time)
    pure_tone = create_pure_tone(1.1, time=time)
    # plt.plot(time, pure_tone)

    # plt.show()

    plot_fourier_transform(signal,
                           pure_tone,
                           plot_center_of_gravity=True,
                           plot_sum=True)

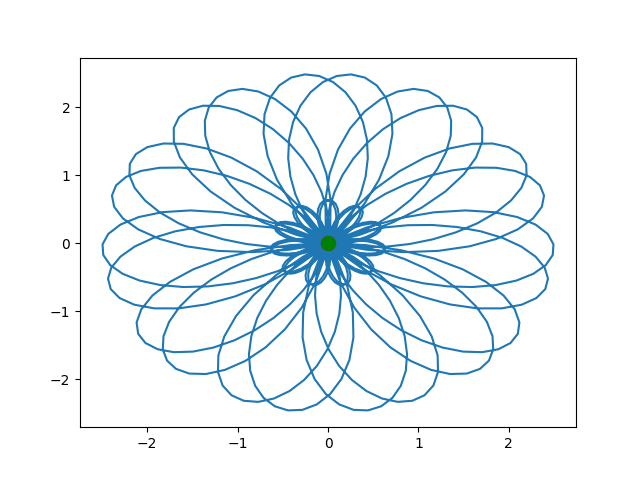
其中 sum 是积分值，center_of_gravity 则是积分值除以采样点的个数，它们都在图中重合了，且积分值为0，所以1.1频率的 $e^{-i2\pi ft}$ 信号与原始信号相似度很低。

当 $e^{-i2\pi ft}$ 信号的频率设置为1时，可得：

if "__main__" == __name__:
    time = np.linspace(0, 10, 1000)
    signal = create_signal(1, time=time)
    pure_tone = create_pure_tone(1.1, time=time)
    # plt.plot(time, pure_tone)

    # plt.show()

    plot_fourier_transform(signal,
                           pure_tone,
                           plot_center_of_gravity=True,
                           plot_sum=False)

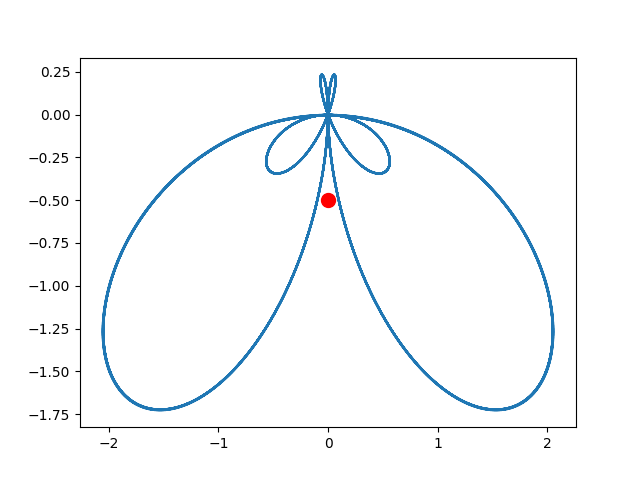
在这里没有把积分值直接放上去，因为值太大了，但是 center_of_gravity 其实就是将 sum 除以采样点的个数，因此可以一定程度上代表 sum。

center_of_gravity 就是 $\hat{g}(f)$ 的运算结果的实部和虚部，都除以采样点的个数，所以不影响辐角，其辐角为$-\frac{\pi }{2}$，这个辐角对于 $e^{-i2\pi ft}$ 信号的频率设置为2或3时，都是一样的：


接下来求出当 $e^{-i2\pi ft}$ 信号的频率设置为1、2、3时，对应的 $c_1,c_2,c_3$：
$$\begin{array}{r}{c}_1=0-j499.5\\ c_2=0-j499.5\\ c_3=0-j499.5\end{array}$$

傅里叶逆变换

傅里叶逆变换的公式可以直接给出：
$$f(t)=\int c_f\cdot e^{i2\pi ft}df$$
从这个形式上看，本质上就是用复数，对不同频率的 $e^{i2\pi ft}$ 信号进行加权求。

傅里叶逆变换的代码与效果如下，注意是对 $e^{i2\pi ft}$ 信号进行加权求和，可以对 $e^{-i2\pi ft}$ 信号取共轭复数得到：

import matplotlib.pyplot as plt
import numpy as np


def create_signal(frequency, time: np.ndarray):
    sin0 = np.sin(2 * np.pi * (frequency * time))
    sin1 = np.sin(2 * np.pi * (2 * frequency * time))
    sin2 = np.sin(2 * np.pi * (3 * frequency * time))

    return sin0 + sin1 + sin2


def create_pure_tone(frequency, time: np.ndarray):
    angle = 2 * np.pi * frequency * time

    return np.cos(angle) - complex(0, 1) * np.sin(angle)


def calculate_mean(multi_signal):
    x_mean = np.mean([x.real for x in multi_signal])
    y_mean = np.mean([x.imag for x in multi_signal])

    return x_mean, y_mean


def calculate_sum(multi_signal):
    x_sum = np.sum([x.real for x in multi_signal])
    y_sum = np.sum([x.imag for x in multi_signal])

    return x_sum, y_sum


def plot_fourier_transform(signal,
                           pure_tone,
                           plot_mean=False,
                           plot_sum=False,
                           plot=True):
    multi_signal = signal * pure_tone
    x_series = np.array([x.real for x in multi_signal])
    y_series = np.array([x.imag for x in multi_signal])

    mean = calculate_mean(multi_signal)
    sum = calculate_sum(multi_signal)

    if plot:
        plt.plot(x_series, y_series)
        if plot_mean:
            plt.plot([mean[0]], [mean[1]],
                     marker='o',
                     markersize=10,
                     color="red")
        if plot_sum:
            plt.plot([sum[0]], [sum[1]],
                     marker='o',
                     markersize=10,
                     color="green")
        plt.show()

    return complex(mean[0], mean[1]), complex(sum[0], sum[1])


def plot_inverse_fourier_transform(cfs, pure_tones, time, plot=True):
    assert len(cfs) == len(pure_tones)
    signal = 0
    for i in range(len(cfs)):
        signal += cfs[i] * np.conj(pure_tones[i])

    if plot:
        plt.plot(time, signal)
        plt.show()

    return signal


if "__main__" == __name__:
    time = np.linspace(0, 10, 1000)
    signal = create_signal(frequency=1, time=time)
    pure_tone0 = create_pure_tone(frequency=1, time=time)
    pure_tone1 = create_pure_tone(frequency=2, time=time)
    pure_tone2 = create_pure_tone(frequency=3, time=time)

    pure_tones = [pure_tone0, pure_tone1, pure_tone2]
    cfs = []
    for pure_tone in pure_tones:
        mean, sum = plot_fourier_transform(signal,
                                           pure_tone,
                                           plot_mean=True,
                                           plot_sum=True,
                                           plot=False)
        cfs.append(sum)

    plot_inverse_fourier_transform(cfs, pure_tones, time)

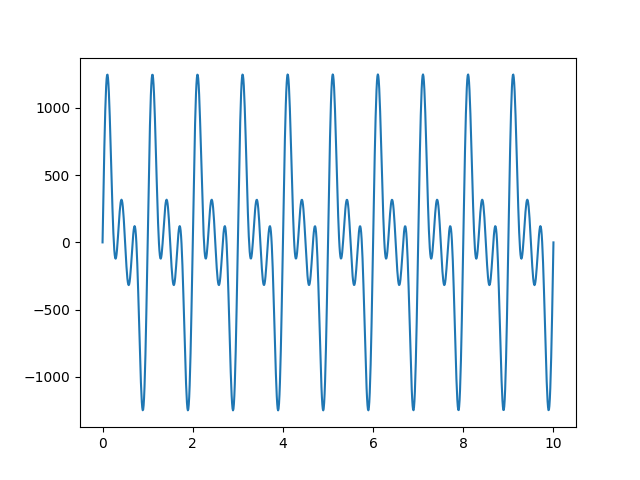
可见其波形与原始信号已经非常相似，但是我们也看出一个明显的问题：为什么幅值比原始信号大了那么多？！

下一部分将与离散傅里叶变换有关，希望能够解释上面的问题。