深入理解傅里叶变换（三）

前情提要

傅里叶变换的公式：
$\hat{F}(f) = \int f(t) e^{-i2 \pi ft} dt$
傅里叶逆变换的公式：
$\int \hat{F}(f) e^{i2 \pi ft} df$

之前我们遇到的问题是：直接用傅里叶逆变换的公式得到的重建信号，幅值要远远大于原始信号。

重建信号
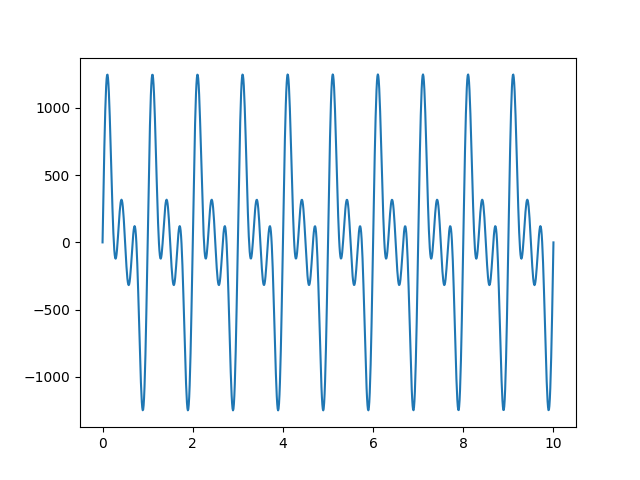
原始信号

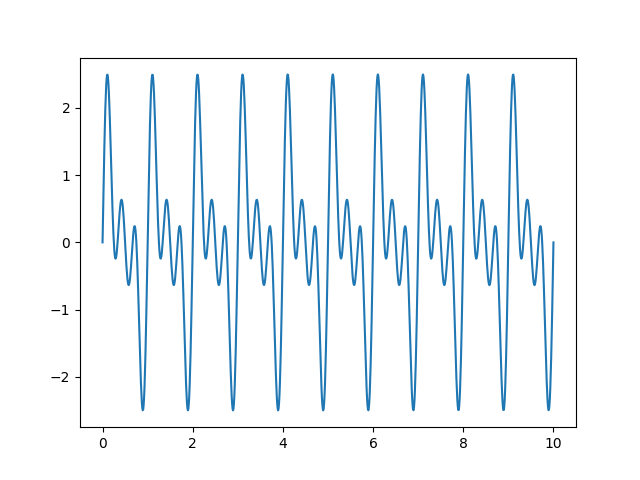
现在可以告诉大家原因：用计算机做的傅里叶变换本质上是离散傅里叶变换，因此要重建信号，也应该用离散傅里叶逆变换。

离散傅里叶变换

傅里叶变换的公式 $\hat{F}(f) = \int f(t) e^{-i2 \pi ft} dt$ 中的 $f (t)$ 表示连续的时序信号，在计算机中会被离散化，即：采样->量化->编码。下图中的T为采样周期，即计算机中每个采样点的间隔时间，数字化之后 $f (t)$ 会变成 $x (n)$ ， $x (n) = f (n T)$ 。
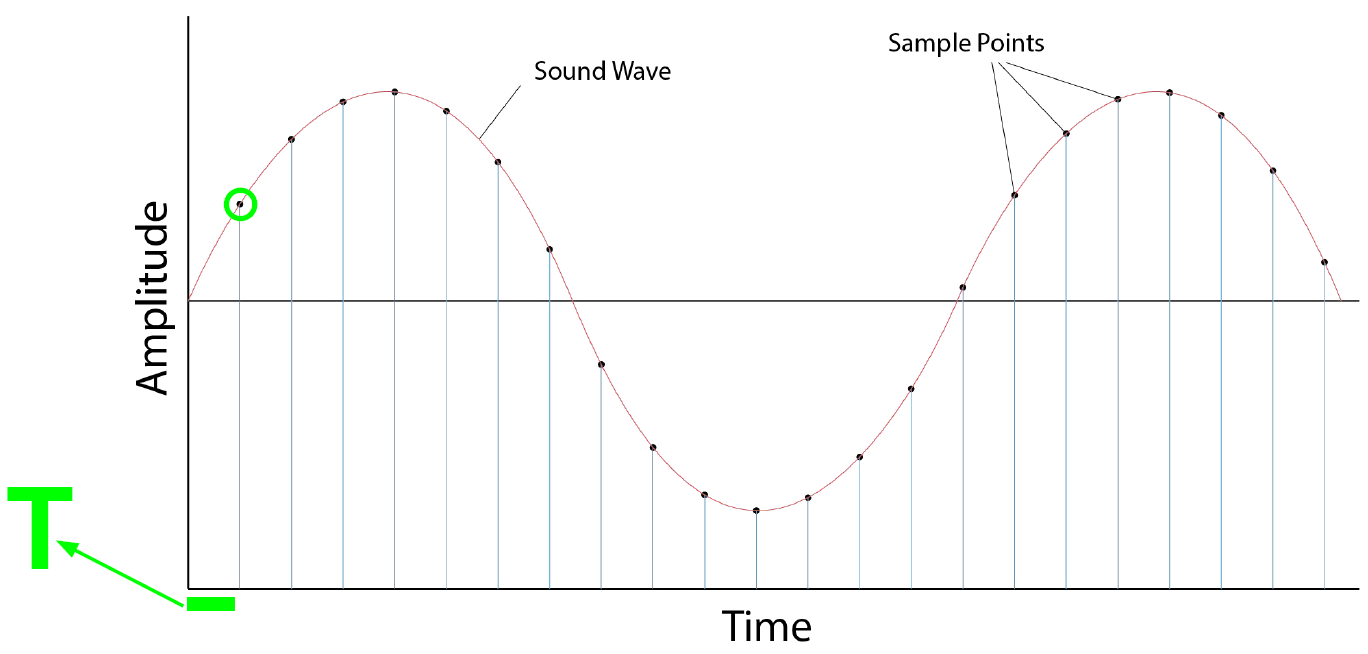
在这里插入图片描述
接下来一步一步将傅里叶变换的公式也离散化：

公式中的信号的符号要变成离散的形式，并且积分符号要变成求和符号
$\hat{X} (f) = \sum_{n} x(n) e^{-i2 \pi fn}$
于是，原始信号和 $e^{-i2 \pi fn}$ 信号都变成了离散形式，变成了可以用下边n访问的一个数组。
还有两个问题：
1. 原始信号在时序上是无穷的，如何在计算机中表示原始信号？
2. 需要选择不同频率的 $e^{-i2 \pi fn}$ 信号，找出对应的最佳振幅和初相，而这些可能的频率也是无穷多个的，如何在计算机中得到这些不同频率的 $e^{-i2 \pi fn}$ 信号呢？
办法还是有的：
1. 假设需要分解的原始信号的频率在一段有限时序区间内是非零的。这个好理解，一首3分钟的歌曲应该已经具有足够的信息，用于频率分解。
  $\hat{X} (f) = \sum_{n=0}^{N-1} x(n) e^{-i2 \pi fn}$
2. 只选取有限个频率，得到有限个 $e^{-i2 \pi fn}$ 信号，对这些有限个信号，找寻最佳的振幅和初相。
3. 所选取的有限个频率的数量，最好与原始信号在一段有限时序区间内的采样点的个数相同，这样做主要是为了能够较好的进行傅里叶逆变换。
  $\hat{X} (\frac{k}{N}) = \sum_{n=0}^{N-1} x(n) e^{-i2 \pi \frac{k}{N}n},k=0,1,2,...,N-1$
4. k的实际含义是什么呢？为何 $\frac{k}{N}$ 能够取代频率f的位置呢？实际上k与f之间存在映射关系，函数表示为：
  $\frac{k}{NT} =\frac{k \cdot s_r}{N}$
  其中sr为原始信号的采样频率。也就是说，所选取的频率范围是[0, sr)，在这范围内，以采样点的个数等分选取频率。

离散傅里叶逆变换

离散傅里叶逆变换的公式可以直接给出：
$\frac{1}{N} \sum_{k=0}^{N-1} \hat{X} (\frac{k}{N}) e^{i2 \pi \frac{k}{N}n}$

import matplotlib.pyplot as plt
import numpy as np


def create_signal(frequency, time: np.ndarray):
    sin0 = np.sin(2 * np.pi * (frequency * time))
    sin1 = np.sin(2 * np.pi * (2 * frequency * time))
    sin2 = np.sin(2 * np.pi * (3 * frequency * time))

    return sin0 + sin1 + sin2


def create_pure_tone(frequency, time: np.ndarray):
    angle = 2 * np.pi * frequency * time

    return np.cos(angle) - complex(0, 1) * np.sin(angle)


def calculate_mean(multi_signal):
    x_mean = np.mean([x.real for x in multi_signal])
    y_mean = np.mean([x.imag for x in multi_signal])

    return x_mean, y_mean


def calculate_sum(multi_signal):
    x_sum = np.sum([x.real for x in multi_signal])
    y_sum = np.sum([x.imag for x in multi_signal])

    return x_sum, y_sum


def plot_fourier_transform(signal,
                           pure_tone,
                           plot_mean=False,
                           plot_sum=False,
                           plot=True):
    multi_signal = signal * pure_tone
    x_series = np.array([x.real for x in multi_signal])
    y_series = np.array([x.imag for x in multi_signal])

    mean = calculate_mean(multi_signal)
    sum = calculate_sum(multi_signal)
    # print(f"mean:{mean}\nsum:{sum}")

    if plot:
        plt.plot(x_series, y_series)
        if plot_mean:
            plt.plot([mean[0]], [mean[1]],
                     marker='o',
                     markersize=10,
                     color="red")
        if plot_sum:
            plt.plot([sum[0]], [sum[1]],
                     marker='o',
                     markersize=10,
                     color="green")
        plt.show()

    return complex(mean[0], mean[1]), complex(sum[0], sum[1])


def plot_inverse_fourier_transform(cfs, pure_tones, time, plot=True):
    assert len(cfs) == len(pure_tones)
    N = len(cfs)
    signal = 0
    for i in range(N):
        signal += cfs[i] * np.conj(pure_tones[i])
    signal /= N

    if plot:
        plt.plot(time, signal)
        plt.show()

    return signal


if "__main__" == __name__:
    time = np.linspace(0, 10, 1000)
    N = time.shape[0]
    sr = 1000 // (10 - 0)

    signal = create_signal(frequency=1, time=time)

    pure_tones = []
    for k in np.linspace(0, N, N, endpoint=False):
        pure_tone = create_pure_tone(frequency=k * sr / N, time=time)
        pure_tones.append(pure_tone)

    cfs = []
    for pure_tone in pure_tones:
        mean, sum = plot_fourier_transform(signal,
                                           pure_tone,
                                           plot_mean=True,
                                           plot_sum=True,
                                           plot=False)
        cfs.append(sum)

    rebuild = plot_inverse_fourier_transform(cfs, pure_tones, time, plot=False)

    plt.plot(time, signal, label="signal")
    plt.plot(time, rebuild, label="rebuild")
    plt.fill_between(time, signal * rebuild, alpha=0.25)
    plt.legend()

    plt.show()

    # np.testing.assert_array_almost_equal(signal, rebuild)

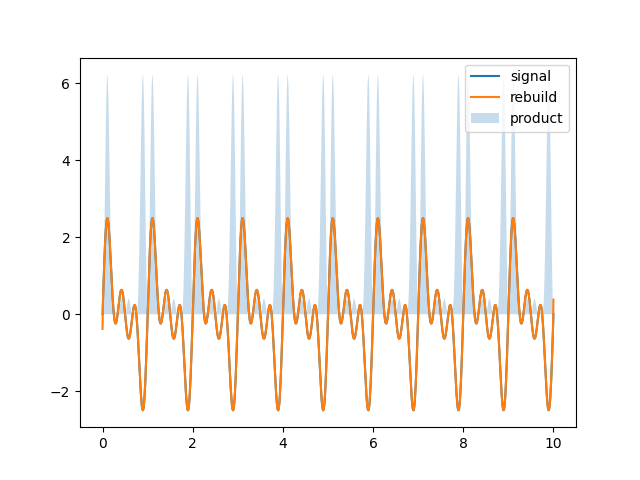
在这里插入图片描述
原始信号与重建信号几乎重合，且乘积也全部为正数！
可以用numpy的单元测试，逐点计算一下误差：

np.testing.assert_array_almost_equal(signal, rebuild)

Arrays are not almost equal to 6 decimals

Mismatched elements: 996 / 1000 (99.6%)
Max absolute difference: 0.00249961
Max relative difference: 1.05935375
 x: array([ 0.000000e+00,  3.758780e-01,  7.428670e-01,  1.092347e+00,
        1.416225e+00,  1.707181e+00,  1.958881e+00,  2.166163e+00,
        2.325182e+00,  2.433514e+00,  2.490210e+00,  2.495807e+00,...
 y: array([ 8.928912e-14-8.203696e-14j,  3.755021e-01-1.757345e-13j,
        7.421241e-01-8.970006e-14j,  1.091254e+00-9.888207e-14j,
        1.414809e+00-5.689618e-15j,  1.705474e+00-3.955452e-15j,...

最大相对误差为1.05935375%。

与numpy比较

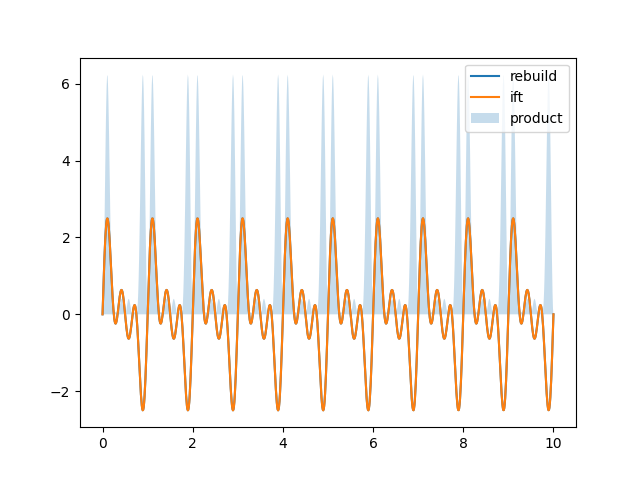
numpy的fft效果极佳，尽管自己写的rebuild与ift波形重合，但ift绝对误差小于小数点后14位。

    # numpy
    ft = np.fft.fft(signal)
    ift = np.fft.ifft(ft)
    plt.plot(time, rebuild, label="rebuild")
    plt.plot(time, ift, label="ift")
    plt.fill_between(time, rebuild * ift, alpha=0.25, label="product")
    plt.legend()

    plt.show()

    np.testing.assert_array_almost_equal(signal, ift, decimal=20)

在这里插入图片描述

Arrays are not almost equal to 20 decimals

Mismatched elements: 1000 / 1000 (100%)
Max absolute difference: 1.875756e-15
Max relative difference: 1.
 x: array([ 0.0000000000000000e+00,  3.7587797360061515e-01,
        7.4286697945743752e-01,  1.0923466914234694e+00,
        1.4162251787527200e+00,  1.7071811899304179e+00,...
 y: array([ 0.0000000000000000e+00-9.2967300524549044e-17j,
        3.7587797360061515e-01-7.7896022965262552e-17j,
        7.4286697945743785e-01+1.0284828544371295e-16j,...

fft的算法复杂度是 $\cdot log_2 N)$ ，只有当采样点数为2的整数次幂时才能运行。

对称性

记得在深入理解傅里叶变换（一）中提到：将选择的频率作为横坐标，对应的波的振幅作为纵坐标，会得到被称为频谱图（spectrum）的东西，如下图所示：

if "__main__" == __name__:
    time = np.linspace(0, 10, 1000)
    sr = 1000 // (10 - 0)
    signal = create_signal(frequency=1, time=time)
    N = signal.size

    pure_tones = []
    frequencies = []
    for k in np.linspace(0, N, N, endpoint=False):
        pure_tone = create_pure_tone(frequency=k * sr / N, time=time)
        pure_tones.append(pure_tone)
        frequencies.append(k * sr / N)

    cfs = []
    for pure_tone in pure_tones:
        mean, sum = plot_fourier_transform(signal,
                                           pure_tone,
                                           plot_mean=True,
                                           plot_sum=True,
                                           plot=False)
        cfs.append(sum)
        print(len(cfs))

    magnitudes = np.abs(cfs)
    rebuild = plot_inverse_fourier_transform(cfs, pure_tones, time, plot=False)
    plt.plot(frequencies, magnitudes, label="spectrum")

    plt.legend()
    plt.show()

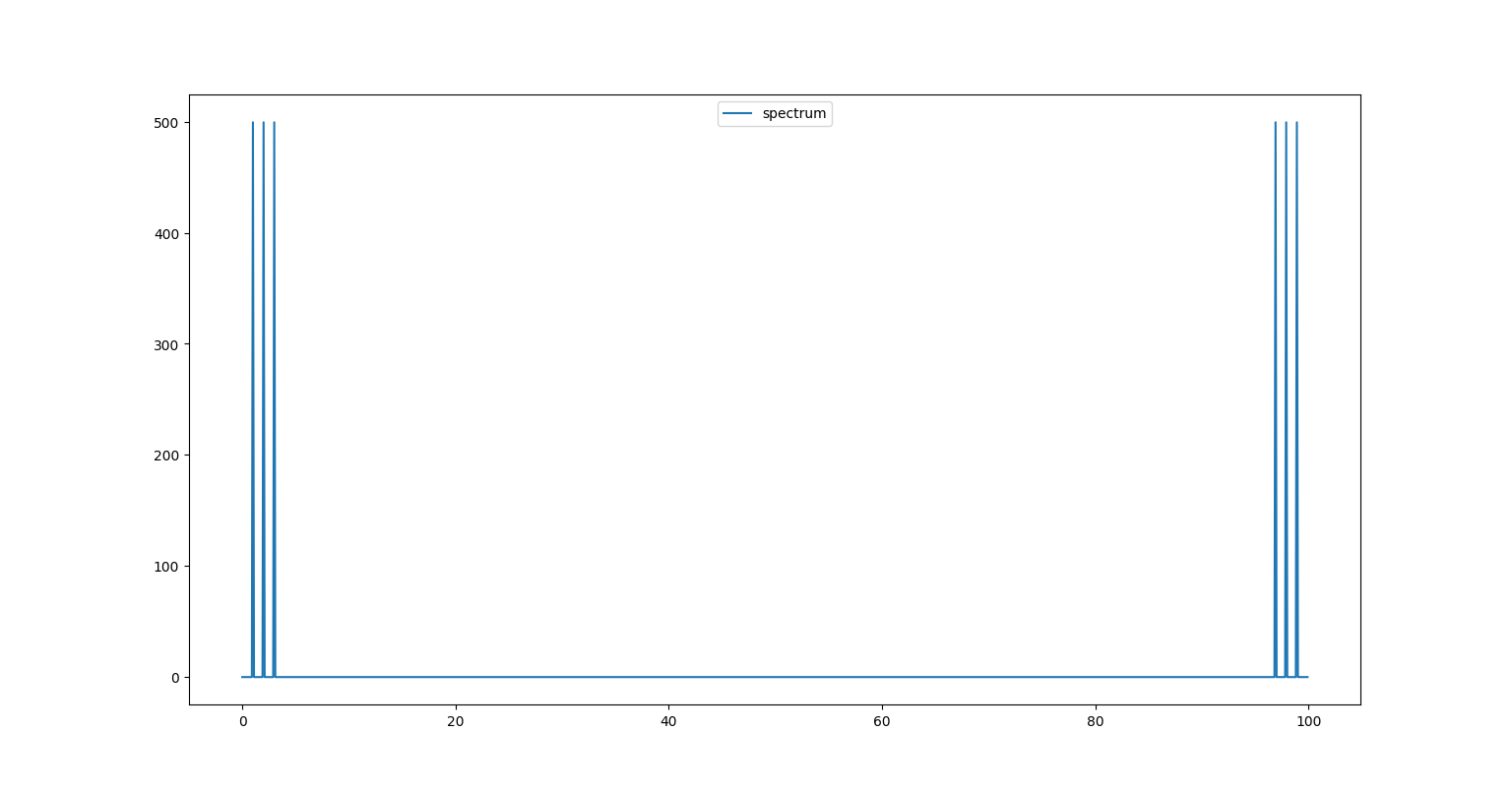
在这里插入图片描述
发现这图是左右对称的，中心是 $\frac{s_r}{2}$ 。

原因是：对于一个周期信号而言，如果想要准确地度量这个信号，则需要在每个周期进行至少两次采样 : 对波峰部分采样一次，对波谷部分采样一次。每个周期的采样越多，越能准确地重建原始信号。但是，如果在每个周期的采样不足两次，那么将完全丢失原始信号的频率信息，也不可能重建原始信号。

现在我们对原始信号的采样率是 $s_r$ ，那么可知这个采样率最多让我们重建原始信号中蕴含的最高频率为 $\frac{s_r}{2}$ 的信号，更高频的信号不可能重建出来。

定理：给定一个采样率，我们所能重建的周期信号的频率是该采样率的一半。该采样率的一半被称为奈奎斯特频率，也就是上图的中心 $\frac{s_r}{2}$ 。

下一节讲短时傅里叶变换。