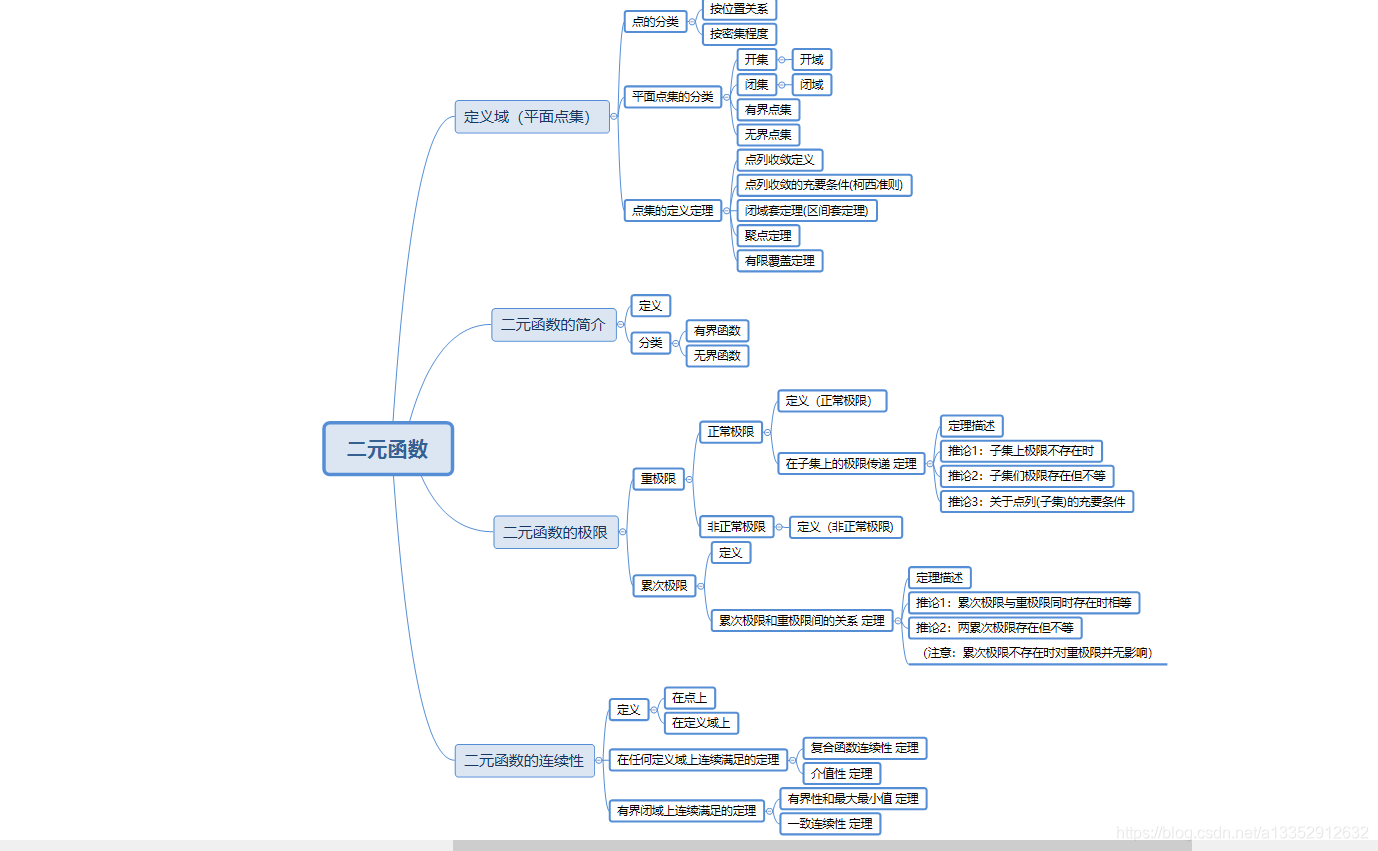
有关定义域
|| 一元函数的定义域是实数轴上的点集,二元函数的定义域是坐标平面上的点集
|| 平面内点A的领域:一般泛指A的方邻域和A的圆邻域
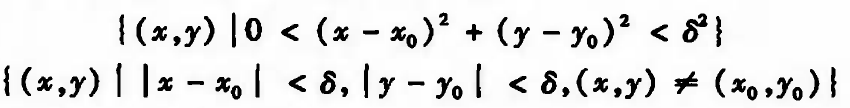
|| 点与点集的关系,按照位置关系可以分为:内点,外点,界点
- 内点:若存在点A的某邻域U(A),使得U(A)包含于E,则称A为E中的内点。E中所有的内点的集合称为E是内部,记作int E
- 外点:若存在点A的某邻域U(A),使得U(A)∩E=空集,则称A为E中的外点。
- 界点:若存在点A的某邻域U(A),使得U(A)中既含有E中的点也含有E外的点,则称A为E中的界点。E的所有的界点的集合称为E的边界。记作∂E
E的界点可能属于E,也可能不属于E,不能说界点就只是点集边界上的点
|| 点和点集的关系,按照密集关系可以分为:聚点,孤立点
- 聚点:若任何点A的空心邻域U(A),都含有E中无穷多个点,则称A为E的聚点 —>类似内点+某些界点
- 孤立点:若A属于E,但不是E的聚点,即U(A) ∩E=空集,则称点A是E的孤立点
|| 两种类型的点之间的关系:
- 聚点 = 所有内点+非孤立的界点
- 孤立点 = 孤立的界点
- 非聚点非孤立点 = 外点
|| 由定义域内的点与点集的关系,定义一些重要的平面点集:
- 开集:若定义域内的所有点都属于E中的内点,则称E为开集
- 闭集:若定义域内的所有聚点都属于E(在e中),则称E为闭集,若点集E没有聚点,也称之为闭集
- 开域:非空连通开集(连通性:E中任意两点都可以用一点完全含于E的有限折现连接)
- 闭域:带边界的非空连通开集
- 区域:开域和闭域,和开域连同其一部分界点所成的点集,统称为区域
全部由><号包围起来的点集为开集
全部由≥≤号包围起来的点集为闭集
半开半闭的点集为非开非闭集(注意不是又闭又开集)
R^2 和 空集,时唯二的又开又闭集
|| 其他关于有界点集的定义:
- 包含关系:对于某一平面E,若存在某一个正数r,使得 E包含于U(O, r),则称E为有界点集。 (其中O是固定点)
- 距离关系:点集E的直径dE(dE = sup d(p1,p2) — 距离最远的两点的距离)为有限值,则称E为有界点集。
点集有关定义定理
|| 定义1:点列收敛定义
设{Pn} 包含于R, 为平面点列,P0属于R 为一固定点。若对任给正数ε,存在正整数N,使得当n大于N时,有Pn属于U(P0, ε), 则称点列{Pn}收敛于P0。
记作:
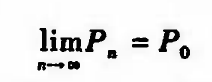
|| 定理1:柯西准则,点列收敛的充要条件
任给正数ε,存在正整数N,使得当n>N时,对一切的正整数p(距离)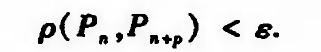
|| 定理2:闭域套定理( 避孕套定理???!!)
设{Dn}是R中的闭域,它满足:
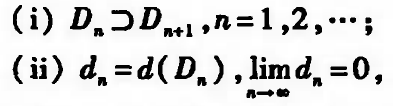
则存在唯一的点P0∈Dn,n=1,2,3…
|| 定理3:聚点定理
设E为有界无限点集,则E在R上至少有一个聚点
(通过闭域套定理证明)
定理3的推论:
有界无限点列{Pn} ,必存在收敛子列{Pn}
|| 定理4:有限覆盖定理
二元函数
|| 定义2:二元函数的定义
设平面点集D,若按照某种对应法则f,D中每一个点P(x, y)都有一个唯一确定的实数z与之对应,则称f为定义在D上的二元函数(或D到R的一个映射),记作: f:D --> R
p的坐标值x,y为函数的因变量
|| 二元函数可以被分为有界函数和无界函数(同一元函数),其充要条件为:

二元函数的极限
|| 定义一:二元函数重极限的定义(正常极限)
设f为D上的二元函数,P0为D的一个聚点,A是一个确定的实数,若给定任意正数ε,总存在某正数δ,使得当P∈U(P0, δ) ∩ D时,都有|f§ - A| < ε, 则称 f 在D上当P->P0时以A为极限,记作
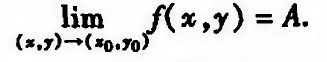
|| 定理5:在子集上的极限连续

- 定理5的推论1:子集极限的不存在
设E1包含于D,P0是E1的聚点,若 f 在E1上P ->P0的极限不存在,那么 f 在D上P->P0的极限也不存在 - 定理5的推论2:子集极限的存在但不等
设E1,E2包含于D,P0是E1,E2的聚点,若在E1,E2上P ->P0的极限存在但不相等,那么f 在D上P->P0的极限不存在 - 定理5的推论3:关于定义域D中某个点列(子集)的充要条件
f 在D上P->P0的极限存在的充要条件为:对于D中任一满足条件Pn != P0且当n->∞时等于P0的点列{Pn},它对应的数列{f(Pn)}收敛
|| 定义二:二元函数重极限的定义(非正常极限 ∞)
二元函数f 的定义域为D,P0为其中的一个聚点,若对任给正数M,总存在某正数δ,使得当P∈U(P0, δ) ∩ D时, 都有f ( P) >M,则称f在D上当P->P0时,存在非正常极限+∞,记作
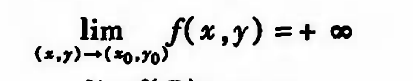
|| 定义三:二元函数累次极限的定义

|| 定理6:累次极限和重极限间的关系
若f(x,y) 中重极限和任一个累次极限(先x后y/先y后x)同时存在,则它们必相等
- 定理6的推论1:
若f(x,y) 中重极限和两个累次极限三者同时存在,则它们必定相等 - 定理6的推论2:
若f(x,y) 中两个累次极限存在但是不相等,则重极限不存在
(注意:累次极限不存在时对重极限并无影响)
二元函数的连续性
定义一:二元函数在某点上连续性定义
设f为定义在点集D包含于R上的二元函数,P0∈D(D的聚点或者孤立点)。对于任给的正数ε,总存在相应的正数δ,只要P∈U(P0,δ)∩D,有:
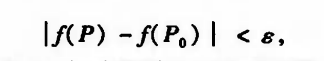
等价于:
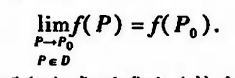
则称 f 关于D上在P0上连续
|| 定义二:二元函数在D上连续性定义
若f在D上的任何点都关于集合D连续,则称f为D上的连续函数
|| 定理7:复合函数的连续性
若函数A = a(x,y),B = b(x,y)连续,则f(A, B)连续
|| 定理8:有界性和最大最小值定理
若f 在有界闭域D上连续,则f 在D上有界,且能取得最大最小值
|| 定理9:一致连续性定理
若f 在有界闭域D上连续,则f 在D上一致连续(即对于任给的正数ε,总存在相应以ε为自变量的正数δ,只要距离d(P, Q)<δ,有:| f§ - f(Q) | < ε (相邻则相同?))
|| 定理10:介值性定理
设f 在 D上连续,P1,P2为D上两点,且f(P1) < f(P2),则对于任何满足f(P1) < u < f(P2) 的实数u,必存在点P0∈D,使得f(P0) = u。
总结:若f连续,则f 符合函数连续,具有介值性,若 f 在有界闭域上仍连续:则f具有有界性,一致连续性
