随机过程基础(4)---各态历经性、典型随机过程matlab仿真

各态历经性部分基础公式源自《随机信号分析与处理》，罗鹏飞等著，清华大学出版社，公式旁有标注*；部分参考资料源自
https://en.wikipedia.org、
http://www.maths.qmul.ac.uk/~bb/TS_Chapter4_3&4.pdf
各态历经部分代码来自
https://www.mathworks.com/help/econ/dtmc.isergodic.html，代码头有标注
(涉及少量随机过程的矩阵表示)

各态历经性（Ergodicity）:
MATLAB检查离散序列的各态历经性有现成函数。
检查马尔可夫链的各态历经性，使用isergodic。（由于随机过程也多用于经济金融类预测分析，应事先下载matlab经济类工具箱，否则无法使用）

设有三阶转移矩阵 $P=\begin{pmatrix}0&1&0\\0&0&1\\1&0&0\end{pmatrix}$执行dtmc函数(discrete-time Markov chain)，并通过ergodic判断是否具有各态遍历性。在复数域得出它的特征值（1，-1/2± $\sqrt{3}i/2$）这个马尔可夫链的周期是3，周期性的马尔可夫过程不是各态历经的。

%这个代码是官方文档里的
 P = [0 1 0; 0 0 1; 1 0 0];
mc = dtmc(P);
isergodic(mc)
eigplot(mc);

设平稳随机过程X(t)，它的时间平均定义
$\overline{m_{X}}=1\cdot i\cdot m\frac{1}{2T}\int_{-T}^{T}X(t)dt$时间相关函数定义 $\overline{R_X(\tau)}=1\cdot i_{T\rightarrow\infty}\cdot m\frac{1}{2T}\int_{-T}^{T}X(t+\tau)X(t)dt$_{***上两式摘自书中}
X是X_n的均方极限，指 $\lim_{x\rightarrow\infty}E\{[X_n-X]^2\}=0$不一个试验，得到的样本函数是不同的，所以时间平均和时间相关函数都不是确定值，可看作随机变量。
对随机序列，需要将积分改为求和，类似随机变量中的情况，求和要除1/2N+1才能得到无偏估计（除1/2N也可以作为量度，但结果是有偏的。（同理，这里的无偏是指多次重复选取样本函数代入公式，计算结果的平均等于事实中的时间平均））。

如果平稳随机过程的时间平均和时间自相关函数依概率收敛到集合平均和集合自相关函数，则X(t)为各态历经过程。

理解各态历经过程：传说中的时间平均，指的是下图temporal averaging，是沿着某次的函数的时间轴（时间趋于正负无穷时）取得的横向平均值；集合平均，指下图的ensemble averaging，是所有样本函数集合在某一特定时刻形成的均值（如果是平稳的，它应该是恒定的）。在下图中，每一时刻都独立同分布（服从μ=1，σ=1的正态分布）。

这里用一个事实例子说明：平稳随机过程各时刻均值恒定，在x=18这个点也要有 $\lim_{M\rightarrow \infty}\frac{1}{M}\sum_{m=1}^Mx_m[18]=E[X[18]]=\mu_X[18]=1$如果时间平均 $\overline{m_{X}}=1\cdot i\cdot m\frac{1}{2T}\int_{-T}^{T}X(t)dt$也收敛到1上，那就爽了。 $\lim_{M\rightarrow \infty}\frac{1}{M}\sum_{m=1}^Mx_m[18]=\lim_{N\rightarrow \infty}\frac{1}{N}\sum_{n=1}^{N-1}x_1[n]$这样就满足了’ergodic in the mean‘，均值遍历性。

这里举一个比较复杂的例子，验证MA随机过程（滑动平均，后面有讲到，可以先看后面）
$X[n]=\frac{1}{2}(U[n]+U[n-1]),-\infty < n<\infty$当 $E[U[n]]=\mu$ $var(U[n])=\sigma_U^2$且U[n]互不相关时，得到的过程具有均值遍历性。将这个变量转化为用协方差矩阵表示，将时间平均的期望值写作

得到a^TC_Xa(i,j)元素是X[i]与X[i]均值差的期望乘X[j]与X[j]均值差的期望。又利用滑动平均随机过程的性质，将差值代换成n和n-1平均值的形式。

便于计算，这里就简化一下，假设U[n]均值为0吧。那么有

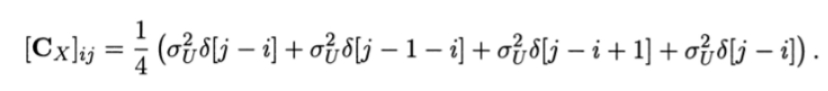
从上可见，对于协方差矩阵的ij元素，当i= j时，是U方差的一半，相差1时为四分之一，相差再多就是0了。可以想象，这是三对角矩阵。求出协方差矩阵后，μ_N的矩估计量就可用本例刚开始的公式求出了。

可见，时间平均依概率收敛于0。所以滑动平均过程具有均值遍历性。

典型非平稳随机过程
在正态随机过程基础上
1.均值随时间变化的

>> randn('state',0)
>> N=51;
>> x = randn (N,1)+0.1*[0:N-1]';

stem([0:N-1],x);

如上图，均值从0增加到 了5
2.方差随时间变化的：

%接着上面
>> y=sqrt(0.95.^[0:50]').*randn(N,1);
stem([0:N-1],y,'diamondr')

方差按照0.95ⁿ指数方式下降。

和随机过程（Sum Random Process）
（上述不是标准术语，方便起见这样称呼）
(以离散情况描述，中括号X[n]表示n只能取离散整数值）

顾名思义，和随机过程就是诸多随机过程的和（把某过程U[1],…,U[i]在每个时刻的样本函数累加）得到的随机过程， $X[n]=\sum_{i=0}^nU[i]$显然也是非平稳的，因为 $E[X[n]]=(n+1)E_U[U[0]]$ $var(X[n])=(n+1)var(U[0])$上式写成n+1纯粹因为n从0开始）
既然是累加得到的，差分就得到原来的U[n]。唯一注意的是，如果U[n]是平稳的，那这就是非平稳变成平稳的方法。更多地， $X[n_2]-X[n_1]=\sum_{i=n_1+1}^{n_2}U[i]$ $X[n_4]-X[n_3]=\sum_{i=n_3+1}^{n_4}U[i]$如果 $n_4\ge n_3\ge n_2\ge n_1$可以认为上两个量还是独立的。（人话，和随机过程不重叠的两个增量是独立的，前提是U[n]独立同分布。）

二项过程（Binomial (counting) process）
假设U[n]是伯努利过程，U[n]=1概率为p，U[n]=0概率1-p，则二项过程 $X[n]=\sum_{i=0}^nU[i]~~~~n=0,1,...$例如， $P[X[1]=1,X[2]=2]=P[Y_1=1,Y_2=1]=P[Y_1=1]P[Y_2=1]$ $=P[U[0]+U[1]=1]P[U[2]=1]$ $=\begin{pmatrix}2\\1\end{pmatrix}p^1(1-p)^1\cdot p$

(正态)白噪声信号（WGN）
随机序列X(n)，X (n)均值为0，自相关函数 $R_X(n_1,n_2)=\sigma_X^2(n_1)\delta(n_1-n_2)$称X(n)为（高斯）白噪声。同一时刻自相关函数恒定称为平稳白噪声。其功率谱为常数（功率谱下面介绍）。平稳白噪声功率谱在整个频率轴上的分布是均匀的，而白光具有均匀的（可见）光谱，因此称为白噪声。
matlab生成（普通）白噪声很简单。

x=randn(500,1);plot(x);

滑动平均过程
它是DTCV（discrete-time continuous-values，随机序列）。 $X[n]=\frac{1}{2}(U[n]+U[n-1]),-\infty < n<\infty$其中U[n]是WGN，方差 $\sigma_U^2$(加下标是为了避免与随机变量中的方差混淆。)例如， $X[0]=\frac{1}{2}(U[0]+U[-1])$ $X[1]=\frac{1}{2}(U[1]+U[0])$下面是用matlab生成滑动平均过程的一段代码：

 randn('state' ,0)
u=randn(21,1);
for i=1:21
	if i==1
		x(i,1)=0.5*(u(1)+randn(1,1)); %needed to initialize sequence
	else
		x(i,1)=0.5*(u(i)+u(i-1)) ;
	end
end
stem([0:20],x(:,1))