This is the hard version of the problem. The only difference between easy and hard versions is the constraint of mm. You can make hacks only if both versions are solved.
Chiori loves dolls and now she is going to decorate her bedroom!
As a doll collector, Chiori has got nn dolls. The ii-th doll has a non-negative integer value aiai (ai<2mai<2m, mm is given). Chiori wants to pick some (maybe zero) dolls for the decoration, so there are 2n2n different picking ways.
Let xx be the bitwise-xor-sum of values of dolls Chiori picks (in case Chiori picks no dolls x=0x=0). The value of this picking way is equal to the number of 11-bits in the binary representation of xx. More formally, it is also equal to the number of indices 0≤i<m0≤i<m, such that ⌊x2i⌋⌊x2i⌋ is odd.
Tell her the number of picking ways with value ii for each integer ii from 00 to mm. Due to the answers can be very huge, print them by modulo 998244353998244353.
Input
The first line contains two integers nn and mm (1≤n≤2⋅1051≤n≤2⋅105, 0≤m≤530≤m≤53) — the number of dolls and the maximum value of the picking way.
The second line contains nn integers a1,a2,…,ana1,a2,…,an (0≤ai<2m0≤ai<2m) — the values of dolls.
Output
Print m+1m+1 integers p0,p1,…,pmp0,p1,…,pm — pipi is equal to the number of picking ways with value ii by modulo 998244353998244353.
Examples
4 4 3 5 8 14
2 2 6 6 0
6 7 11 45 14 9 19 81
1 2 11 20 15 10 5 0
tutorial:
Build linear basis AA with given numbers. Suppose:
- kk is the length of AA.
- S(A)S(A) is the set consisted of numbers which can be produced in AA.
- pipi is equal to the number of xx, where x∈S(A)x∈S(A) and popcount(x)=ipopcount(x)=i.
- ansiansi is equal to the number of doll picking ways with value ii. Thus, ansi=pi⋅2n−kansi=pi⋅2n−k.
Algorithm 1
Enumerate each base of AA is picked or not, so you can find out the whole S(A)S(A) in O(2k)O(2k) and get p0…pmp0…pm. Note that you should implement popcount(x)popcount(x) in O(1)O(1) to make sure the whole algorithm runs in O(2k)O(2k).
Algorithm 2
Let's assume the highest 11-bits in every base are key bits, so in AA there are kk key bits and m−km−k non-key bits. We can get a new array of bases by Gauss-Jordan Elimination, such that every key bit is 11 in exactly one base and is 00 in other bases.
Then, let fi,j,sfi,j,s be if we consider the first ii bases in AA, the number of ways that jj key bits are 11 in xor-sum and the binary status of all non-key bits is ss. Enumerate ii-th base (suppose it is equal to xx) is picked or not, we write the state transition: fi,j,s=fi−1,j,s+fi−1,j−1,s⊕xfi,j,s=fi−1,j,s+fi−1,j−1,s⊕x.
At last, we add up fk,j,sfk,j,s to pj+popcount(s)pj+popcount(s). In conclusion, we get an O(k2⋅2m−k)O(k2⋅2m−k) algorithm.
So far, the easy version can be passed if you write a solution which runs Algorithm 1 or Algorithm 2 by the value of kk.
Algorithm 3
We can regard AA as a 2m2m long zero-indexation array satisfying ai=[i∈S(A)]ai=[i∈S(A)]. Similarly, we define a 2m2m long zero-indexation array FcFc satisfying fci=[popcount(i)=c]fic=[popcount(i)=c].
By XOR Fast Walsh-Hadamard Transform, we calculate IFWT(FWT(A)∗FWT(Fc))IFWT(FWT(A)∗FWT(Fc)) (also can be written as A⊕FcA⊕Fc). pcpc is equal to the 00-th number of resulting array. That means pcpc is also equal to the sum of every number in FWT(A)∗FWT(Fc)FWT(A)∗FWT(Fc)divide 2m2m.
Lemma 1: FWT(A)FWT(A) only contains two different values: 00 and 2k2k.
Proof: The linear space satisfies closure, which means A⊕A=A∗2kA⊕A=A∗2k. Thus, FWT(A)∗FWT(A)=FWT(A)∗2kFWT(A)∗FWT(A)=FWT(A)∗2k. We can proved the lemma by solving an equation.
Lemma 2: The ii-th number of FWT(A)FWT(A) is 2k2k, if and only if popcount(i & x)popcount(i & x) is always even, where xx is any of kk bases in AA.
Proof: XOR Fast Walsh-Hadamard Transform tells us, the ii-th number of FWT(A)FWT(A) is equal to the sum of (−1)popcount(i & j)(−1)popcount(i & j) for each j∈S(A)j∈S(A). Once we find a base xx such that popcount(i & x)popcount(i & x) is odd, the sum must be 00 according to Lemma 1.
Lemma 3: The indices of FWT(A)FWT(A) which their values are 2k2k, compose an orthogonal linear basis.
Proof: See Lemma 2. If popcount(i & x)popcount(i & x) is even, popcount(j & x)popcount(j & x) is even, obviously popcount((i⊕j) & x)popcount((i⊕j) & x) is even.
Suppose BB is the orthogonal linear basis. It can be proved that the length of BB is m−km−k. In other words, the key bits in AA are non-key bits in BB and the non-key bits in AA are key bits in BB. I'll show you how to get the m−km−k bases in BB.
Divide key bits for AA and put them to the left. Similarly, we put the key bits in BB to the right. Let's make those 11 key bits form a diagonal.
Look at the following picture. Do you notice that the non-key bit matrices (green areas) are symmetrical along the diagonal?
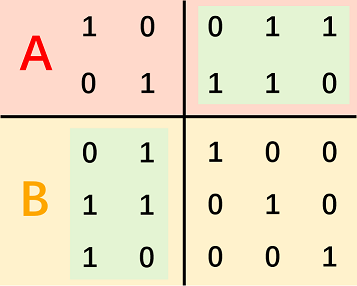
The proof is intuitive. popcount(x & y)popcount(x & y) should be even according to Lemma 2, where xx is any of bases in AA and yy is any of bases in BB. Since we've divided key bits for two linear basis, popcount(x & y)popcount(x & y) is not more than 22. Once two symmetrical non-key bits are 00, 11 respectively, there will exist xx, yy satisfying popcount(x & y)=1popcount(x & y)=1. Otherwise, popcount(x & y)popcount(x & y) is always 00 or 22.
In order to get BB, you can also divide AA into kk small linear basis, construct their orthogonal linear basis and intersect them. It is harder to implement.
Lemma 4: The ii-th number of FWT(Fc)FWT(Fc) only depends on popcount(i)popcount(i).
Proof: The ii-th number of FcFc only depends on popcount(i)popcount(i), it certainly still holds after Fast Walsh-Hadamard Transform.
Let wcdwdc be the (2d−1)(2d−1)-th number of FWT(Fc)FWT(Fc). Again, Fast Walsh-Hadamard Transform tells us:
- wcd=∑i=02m−1[popcount(i)=c](−1)popcount(i & (2d−1))wdc=∑i=02m−1[popcount(i)=c](−1)popcount(i & (2d−1))
Note that popcount(2d−1)=dpopcount(2d−1)=d. Let's enumerate j=popcount(i & (2d−1))j=popcount(i & (2d−1)). There are (dj)(dj) different intersections, each one has (m−dc−j)(m−dc−j) ways to generate the remaining part of ii. So:
- wcd=∑j=0d(−1)j(dj)(m−dc−j)wdc=∑j=0d(−1)j(dj)(m−dc−j)
It takes O(m3)O(m3) to calculate all necessary combinatorial numbers and wcdwdc.
Finally, let's consider the sum of every number in FWT(A)∗FWT(Fc)FWT(A)∗FWT(Fc). Suppose qiqi is equal to the number of xx, where x∈S(B)x∈S(B) and popcount(x)=ipopcount(x)=i. We can easily get:
- pc=12m∑d=0m2kqdwcd=12m−k∑d=0mqdwcdpc=12m∑d=0m2kqdwdc=12m−k∑d=0mqdwdc
Just like Algorithm 1. We can enumerate each base of BB is picked or not, find out the whole S(B)S(B) in O(2m−k)O(2m−k), get q0…qmq0…qm and calculate p0…pmp0…pm at last. Since one of AA, BB has a length of not more than m/2m/2, we just need to enumerate bases of the smaller one in order to pass the hard version in O(2m/2+m3+n)O(2m/2+m3+n).
solution:
#include <bits/stdc++.h> using namespace std; using i64 = long long; const int maxN = 223456; const int P = 998244353; int n, m, rnk; i64 base[maxN], p[maxN], dp[60][60][2]; int cnt[maxN], ans[maxN]; void dfs1(int d, i64 x) { if (d == rnk) { cnt[__builtin_popcountll(x)]++;//__builtin_popcountll()返回‘1’的个数 } else { dfs1(d + 1, x); dfs1(d + 1, x ^ p[d]); } } int main() { scanf("%d%d", &n, &m); for (int i = 0; i < n; i++) { i64 x; scanf("%lld", &x); for (int j = m - 1; j >= 0; j--) { if (base[j]) { x = min(x, base[j] ^ x); } else if (x & (1ll << j)) { base[j] = x; p[rnk++] = x; break; } } } if (rnk <= m / 2) { dfs1(0, 0); i64 multi = 1; for (int i = 0; i < n - rnk; i++) multi = multi * 2 % P; for (int i = 0; i <= m; i++) { printf("%lld ", cnt[i] * multi % P); } } else { for (int i = m - 1; i >= 0; i--) { for (int j = i - 1; j >= 0; j--) base[i] = min(base[i], base[i] ^ base[j]); } rnk = 0; for (int i = 0; i < m; i++) if (base[i] == 0) { i64 x = (1ll << i); for (int j = i + 1; j < m; j++) if (base[j] & (1ll << i)) { x ^= (1ll << j); } p[rnk++] = x; } dfs1(0, 0); for (int x = 0; x <= m; x++) { memset(dp, 0, sizeof(dp)); dp[0][0][0] = 1; for (int j = 0; j < m; j++) for (int k = 0; k <= m; k++) for (int par = 0; par <= 1; par++) { dp[j + 1][k + 1][par ^ (j < x)] += dp[j][k][par]; dp[j + 1][k][par] += dp[j][k][par]; } for (int k = 0; k <= m; k++) { i64 w = dp[m][k][0] - dp[m][k][1]; w %= P; if (w < 0) w += P; ans[k] = (ans[k] + cnt[x] * w) % P; } } i64 multi = 1; for (int i = 0; i < n; i++) multi = multi * 2 % P; for (int i = 0; i < m; i++) multi = multi * (P + 1) / 2 % P; for (int i = 0; i <= m; i++) { printf("%lld ", ans[i] * multi % P); } } }