CF1336E Chiori and Doll Picking 【线性代数，组合计数】

题目描述：给定 $n$ 个数 $a_i\in[0,2^m)$，对所有 $k=0,1,\dots,m$，求 $\sum_{S\in \{a_i\}}[\text{popcount}(\bigoplus_{x\in S}x)=k]$。

数据范围：$n\le 2\cdot 10^5,m\le 53$。部分分 $m\le 35$。

本文参考官方题解。

设 $A$ 是给出的数得到的线性基，$\text{span}(A)$ 表示 $A$ 张成的线性空间， $F(S)=\sum_{x\in\text{span}(S)}z^x$，$P(S)=\sum_{x\in\text{span}(S)}z^{\text{popcount}(x)}$。

设 $\langle i,j\rangle=\text{popcount}(i\text{ and } j)$。生成函数乘法默认 xor 卷积。

则 $\langle i,k\rangle+\langle j,k\rangle\equiv \langle i\oplus j,k\rangle (\text{mod} \ 2)$，即乘法（and）关于加法（xor）的分配律。

首先大家肯定都会 $O(2^{\text{rank}(A)})$，即枚举线性基的子集。

对于 $m\le 35$，直接用 meet-in-the-middle，把线性基分成高位和低位两部分，其中低位部分只有在最低 $ \lceil\frac{m}{2}\rceil$ 位有值。设 $f_{i,S}$ 表示对于高位的线性基异或出来的所有值，较高 $\lfloor\frac{m}{2}\rfloor$ 位的 popcount 为 $i$，较低 $\lceil\frac{m}{2}\rceil$ 为 $S$ 的方案数。$g_S$ 表示低位的线性基异或出 $S$ 的方案数。将 $m$ 个 $f_i$ 与 $g$ 做 xor 卷积合并即可。复杂度 $O(m2^{\lceil\frac{m}{2}\rceil}+m^22^{\lfloor\frac{m}{2}\rfloor})$。

结果这个做法对满分做法没有一点用处（

满分做法使用了根号分治的思想，对于 $\text{rank}(A)\le \lfloor\frac{m}{2}\rfloor$ 时使用暴力，对于其他情况考虑寻找一个 $O(2^{m-\text{rank}(A)})$ 的做法。

有线性基的一些性质得到：

第一行：线性空间 做 线性空间内的线性变换 得到它自己。
第二行：乘法分配律。
第三、四行：做 FWT。根据这个柿子就可以知道，$\text{FWT}(F(A))$ 的每一位是 $0$ 或 $2^{\text{rank}(A)}$。
第五、六行：如果存在一个 $x$ 使得 $2\not|\langle k,x\rangle$，则该位不可能为 $2^{\text{rank}(A)}$，只能为 $0$。

\[\begin{align*}(z^x)\times F(A)&=F(A) & x\in\text{span}(S) \\F(A)\times F(A)&=F(A)\cdot 2^{\text{rank}(A)} \\\text{FWT}(F(A))\cdot\text{FWT}(F(A))&=\text{FWT}(F(A))\cdot 2^{\text{rank(A)}} \\ [z^k]\text{FWT}(F(A))&=\sum_{x\in\text{span}(A)}(-1)^{\langle k,x\rangle}\\&=2^{\text{rank}(A)}[\forall x\in\text{span}(A),2|\langle k,x\rangle] \\&=2^{\text{rank}(A)}[\forall x\in A,2|\langle k,x\rangle]\end{align*} \]

定义 $A$ 的正交线性基为 $B$，使得 $\forall x\in A,y\in B$，$2|\langle x,y\rangle$。并且 $\text{rank}(A)+\text{rank}(B)=m$。

则 $F(B)\cdot 2^{\text{rank}(A)}=\text{FWT}(F(A))$。

至于它怎么求，你可以把线性基中的列进行一些交换，使得它的左边是一个边长 $\text{rank}(A)$ 的单位矩阵。

然后将右边一个矩形对称到它的左下方，右下方是一个边长为 $m-\text{rank}(A)$ 的单位矩阵。

（放一个官方题解的图）

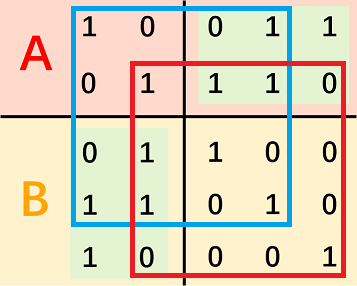
很容易检验它就是 $A$ 的正交线性基，并且两两之间的 $\langle x,y\rangle\in\{0,2\}$。

求出正交线性基之后呢，考虑算答案。设 $G_c=\sum_{x\ge 0}z^x[\text{popcount}(x)=c]$。

\[\begin{align*} [z^c]P(A)&=[z^0](A\times G_c) \\ &=[z^0]\text{IFWT}(\text{FWT}(F(A))\cdot\text{FWT}(G_c)) \end{align*} \]

\[[z^0]\text{IFWT}(X)=2^{-m}\sum_{i\ge 0}[z^i]X \]

我们知道 $\text{FWT}(F(A))=F(B)\cdot 2^{\text{rank}(A)}$。

\[[z^c]P(A)=2^{\text{rank}(A)-m}\sum_{d\ge 0}[z^d]P(B)\sum_{i\ge 0}(-1)^i\binom{d}{i}\binom{m-d}{c-i} \]

（$d$ 为枚举 $F(B)$ 中每一项的大小，$i$ 是 FWT 时的两个集合的交集大小）

直接计算，时间复杂度 $O(2^{\lfloor\frac{m}{2}\rfloor}+mn+m^3)$。

总而言之，正交线性基是一个与原线性基“互补”的东西，同时反映了原线性基的性质。也就找到了 $O(2^{m-\text{rank}(A)})$ 的做法。

#include<bits/stdc++.h>
#define Rint register int
using namespace std;
typedef long long LL;
const int N = 63, mod = 998244353;
template<typename T>
inline void read(T &x){
    int ch = getchar(); x = 0;
    for(;ch < '0' || ch > '9';ch = getchar());
    for(;ch >= '0' && ch <= '9';ch = getchar()) x = x * 10 + ch - '0';
}
template<typename T>
inline bool chmin(T &a, const T &b){if(a > b) return a = b, 1; return 0;}
template<typename T>
inline bool chmax(T &a, const T &b){if(a < b) return a = b, 1; return 0;}
inline int ksm(int a, int b){
    int res = 1; if(b < 0) b += mod - 1;
    while(b){
        if(b & 1) res = (LL) res * a % mod;
        a = (LL) a * a % mod; b >>= 1;
    }
    return res;
}
inline void qmo(int &x){x += (x >> 31) & mod;}
LL lb[N], a[N], b[N], p[N];
int n, m, k, C[N][N];
inline void insert(LL x){
    for(Rint i = m - 1;~i;-- i) if((x >> i) & 1){
        if(!lb[i]){lb[i] = x; return;}
        x ^= lb[i];
    }
}
inline void dfs(int dep, LL x){
    if(dep == k){++ p[__builtin_popcountll(x)]; return;}
    dfs(dep + 1, x); dfs(dep + 1, x ^ a[dep]);
}
int main(){
    read(n); read(m);
    for(Rint i = 1;i <= n;++ i){
        LL x; read(x); insert(x);
    }
    for(Rint i = 0;i < m;++ i)
        if(lb[i]){
            for(Rint j = i - 1;~j;-- j)
                if((lb[i] >> j) & 1) lb[i] ^= lb[j];
        }
    for(Rint i = 0;i < m;++ i)
        if(lb[i]){
            for(Rint j = 0;j < m;++ j)
                if(!lb[j]) a[k] = (a[k] << 1) | (lb[i] >> j & 1);
            a[k] |= (1ll << m - 1 - k); ++ k;
        }
    if(k <= (m >> 1)){
        dfs(0, 0); int tmp = ksm(2, n - k);
        for(Rint i = 0;i <= m;++ i) printf("%lld ", p[i] * tmp % mod);
    } else {
        for(Rint i = 0;i < m - k;++ i){
            for(Rint j = 0;j < k;++ j)
                if((a[j] >> i) & 1)
                    b[i] |= (1ll << j);
            b[i] |= (1ll << m - 1 - i);
        }
        swap(a, b); k = m - k;
        dfs(0, 0); int tmp = ksm(2, n - m);
        C[0][0] = 1;
        for(Rint i = 1;i <= m;++ i){
            C[i][0] = 1;
            for(Rint j = 1;j <= i;++ j)
                qmo(C[i][j] = C[i - 1][j] + C[i - 1][j - 1] - mod);
        }
        for(Rint c = 0;c <= m;++ c){
            int ans = 0;
            for(Rint d = 0;d <= m;++ d){
                int tt = 0;
                for(Rint i = 0;i <= c;++ i){
                    int ttt = (LL) C[d][i] * C[m - d][c - i] % mod;
                    if(i & 1) qmo(tt -= ttt);
                    else qmo(tt += ttt - mod);
                }
                qmo(ans += (LL) tt * p[d] % mod - mod);
            }
            printf("%lld ", (LL) ans * tmp % mod);
        }
    }
}

CF1336E Chiori and Doll Picking 【线性代数，组合计数】

猜你喜欢